03-树1 树的同构

Posted 2021-01-13 shin0324

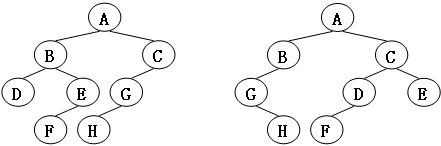
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 

 

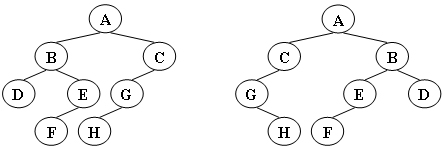
图1

图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N?1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2：

No

几组测试数据：


• 测试点0：sample 1 有双边换、单边换，节点编号不同但数据同8
  A 1 2
  B 3 4
  C 5 -
  D - -
  E 6 -
  G 7 -
  F - -
  H - -
  8
  D - -
  E 7 -
  B 1 0
  A 4 2
  C 5 -
  G - 6
  H - -
  F - -
• 测试点1：sample 2 第3层开始错，每层结点数据对，但父结点不对
  8
  A 1 2
  B 3 4
  C 5 -
  D - -
  E 6 -
  G 7 -
  F - -
  H - -
  8
  A 1 2
  B 3 4
  C - 5
  D - 6
  E - -
  G 7 -
  F - -
  H - -
• 测试点2：结点数不同
  8
  A 1 2
  B 3 4
  C 5 -
  D - -
  E 6 -
  G 7 -
  F - -
  H - -
  9
  D - -
  E 7 -
  B 1 0
  A 4 2
  C 5 -
  G - 6
  H - -
  F - 8
  I - -
• 测试点4：只有1个结点，结构同但数据不同
  1
  3 - -
  1
  5 - -
• 测试点5：最大N，层序遍历结果相同，但树不同
  10
  A 1 2
  B 3 4
  C 5 6
  D 7 8
  E 9 -
  F - -
  G - -
  H - -
  I - -
  J - -
  10
  A 1 2
  B 3 4
  C 5 6
  D 7 -
  E 8 9
  F - -
  G - -
  H - -
  I - -
  J - -

 1 //一种投机取巧的方法??
 2 //题目说明“如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是同构的。”
 3 //也就是说同构只是进行左右孩子的互换，即每个节点的子节点都是确定的，只是左右位置在变
 4 //从而只需要对照T2每个节点的子节点与T1同一个节点的子节点是否相同，就可判断是否是同构
 5 
 6 #include<stdio.h>
 7 #define max 11
 8 #define Null -1
 9 typedef struct TNode *PtrToTNode;
10 struct TNode{
11     char data;
12     int right, left;
13 }T1[max], T2[max];
14 typedef PtrToTNode Tree;
15 
16 void ReadTree(Tree T, int N){
17     for(int i=0; i<N; i++){
18         char data, left, right;
19         scanf("
%c %c %c", &data, &left, &right);
20         T[i].data = data;
21         if(left==‘-‘){
22             T[i].left = Null;
23         }
24         else T[i].left = left - ‘0‘;
25         if(right==‘-‘){
26             T[i].right = Null;
27         }
28         else T[i].right = right - ‘0‘;
29     }
30 }
31 
32 bool cmp(Tree T1, Tree T2, int N1, int N2){
33     int i, j;      
34     bool flag2 = true;
35     if(N1!= N2)  flag2 = false;
36     for(i=0; i<N2 && flag2; i++){  //如果还没遍历完T2，并且前面没有确定T2不可能与T1同构         
37         int flag1 = 0;             //flag1记录该节点是否符合需要的条件，flag1要定义在for循环里或者每次更新回0
38         for(j=0; j<N1; j++) {        
39             if(T1[j].data==T2[i].data) {       //找到T1中data相同的节点 
40                 if((T1[T1[j].left].data==T2[T2[i].left].data && T1[T1[j].right].data==T2[T2[i].right].data)  //如果T2的节点与T1节点的子节点位置相同且相等 
41                 || (T1[T1[j].right].data==T2[T2[i].left].data && T1[T1[j].left].data==T2[T2[i].right].data)) //或位置相反，data相等 
42                 {                                                               
43                     flag1 = 1;            //找到了data相同且子节点相同的节点
44                 }
45                 break;
46             }
47         }
48         if(!flag1) {          //如果从上一个循环中出来并没有找到data相同且子节点相同的节点 
49             flag2 = false;    //即T2不可能与T1同构 
50         }
51     }
52     return flag2;
53 }
54 
55 //主程序框架 
56 int main( ){
57     int N1, N2;
58     bool flag;
59     scanf("%d", &N1);
60     ReadTree(T1, N1);
61     scanf("%d", &N2);
62     ReadTree(T2, N2);
63     if(cmp(T1, T2, N1, N2)) printf("Yes
");
64     else printf("No
");
65     return 0;
66 }

 1 //常规方法，建树，然后递归比较每个子树 
 2 #include<stdio.h> 
 3 #define max 11
 4 #define Null -1          //Null定义为-1而不是0，因为T[0]是有元素的 
 5 struct TNode{
 6     char data;
 7     int left, right;    
 8 }T1[max], T2[max];
 9 typedef struct TNode *Tree;
10 
11 int BuildTree(Tree T){
12     int N, i, root = Null;
13     char Data, L, R;
14     scanf("%d", &N);
15     int check[N] = {0};
16     for(i=0; i<N; i++){
17         scanf("
%c %c %c", &Data, &L, &R);
18         T[i].data = Data;
19         if(L == ‘-‘){
20             T[i].left = Null;
21         }
22         else {
23             T[i].left = L-‘0‘;
24             check[L-‘0‘] = 1;
25         }
26         if(R == ‘-‘){
27             T[i].right = Null;
28         }
29         else {
30             T[i].right = R-‘0‘;
31             check[R-‘0‘] = 1;
32         }
33     }
34     for(i=0; i<N; i++){
35         if(check[i]==0) {
36             root = i;
37             break;
38         }
39     }
40     return root;
41 }
42 
43 bool cmp(int t1, int t2){
44     if(t1==Null && t2==Null){         //两树均为空，是同构 
45         return true;
46     }
47     if(t1==Null || t2==Null){         //一空一不空，一定不是同构 
48         return false;
49     }
50     if(T1[t1].data != T2[t2].data){   //两树头节点不相等，一定不是同构 
51         return false;
52     }
53     if(T1[t1].left == Null && T2[t2].left == Null){     //两树左子树都为空 
54         return (cmp(T1[t1].right, T2[t2].right));       //递归地比较右子树 
55     }
56     if(T1[t1].left != Null && T2[t2].left != Null && T1[T1[t1].left].data == T2[T2[t2].left].data){  //两树左子树非空且相等 
57         return (cmp(T1[t1].left, T2[t2].left) && cmp(T1[t1].right, T2[t2].right));    //递归地比较左子树的子树 和 右子树 
58     }
59     else{                                                                            //两树左子树不相等 
60         return (cmp(T1[t1].left, T2[t2].right) && cmp(T1[t1].right, T2[t2].left));   //互换左右子树进行比较 
61     }
62 }
63 
64 //主程序框架 
65 int main( ){
66     int t1, t2;         //t1, t2是树的根节点的下标 
67     t1 = BuildTree(T1);
68     t2 = BuildTree(T2);
69     if(cmp(t1, t2)) printf("Yes
");
70     else printf("No
");
71 }