optics聚类算法
Posted simplex
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了optics聚类算法相关的知识,希望对你有一定的参考价值。
前段时间需要对一些客服对话记录做聚类分析,于是抽时间测试了一下常见聚类算法的效果。之前了解过的聚类算法大多在sklearn中都有现成的实现可以直接用,不过optics算法倒没找到,于是就看着论文做了个简易版的。下面是算法源码,关于原理请参考原始论文:
- C. Ding, X. He, and H. D. Simon, “On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering,” in Proceedings of the 2005 SIAM International Conference on Data Mining, H. Kargupta, J. Srivastava, C. Kamath, and A. Goodman, Eds. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2005, pp. 606–610.
verbose.py:辅助调试用
1 class Verbose: 2 def __init__(self, verbose): 3 self.set_printer(verbose) 4 5 def set_printer(self, verbose): 6 if verbose: 7 self.printer = print 8 else: 9 self.printer = lambda x: None
tree.py:定义了二叉树的基本操作
1 # -*- coding: utf-8 -*- 2 3 class Node: 4 def __init__(self, data=None, left=None, right=None): 5 self.data = data 6 self.left = left 7 self.right = right 8 9 @property 10 def is_leaf(self): 11 """如果没有左右子节点,就是叶子节点 12 13 :returns: 14 :rtype: 15 16 """ 17 18 return (not self.left) and (not self.right) 19 20 def preorder(self): 21 """先序遍历递归版本 22 遍历顺序为root->left->right 23 :returns: 24 :rtype: 25 26 """ 27 28 if not self: 29 return 30 31 yield self 32 33 if self.left: 34 for x in self.left.preorder(): 35 yield x 36 37 if self.right: 38 for x in self.right.preorder(): 39 yield x 40 41 def preorder_norecur(self): 42 """先序遍历非递归版本 43 遍历顺序为root->left->right 44 :returns: 45 :rtype: 46 47 """ 48 49 if not self: 50 return 51 stack = [self] 52 while stack: 53 node = stack.pop() 54 yield node 55 ## 后入先出 56 if node.right: 57 stack.append(node.right) 58 if node.left: 59 stack.append(node.left) 60 61 def inorder(self): 62 """中序遍历递归版本 63 遍历顺序为left->root->right 64 :returns: 65 :rtype: 66 67 """ 68 if not self: 69 return 70 71 if self.left: 72 for x in self.left.inorder(): 73 yield x 74 75 yield self 76 77 if self.right: 78 for x in self.right.inorder(): 79 yield x 80 81 def inorder_norecur(self): 82 """中序遍历非递归版本 83 遍历顺序为left->root->right 84 85 :returns: 86 :rtype: 87 中序遍历的思路是先一直找到最左子节点,把沿途所有节点都入栈, 88 然后开始出栈,出栈之后把当前节点设置为上一个节点的右子节点, 89 进行右子树的遍历(如果右子树为空显然就免于遍历了) 90 91 """ 92 93 if not self: 94 return 95 96 stack = [] 97 98 node = self 99 100 while node is not None or len(stack) > 0: 101 if node is not None: 102 stack.append(node) 103 node = node.left 104 else: 105 # 如果node是叶子节点,那么node.right==None,下次会继续弹出node的父节点 106 # 如果node不是叶子节点,且node.right非空,那么下次会执行入栈操作 107 node = stack.pop() 108 yield node 109 node = node.right 110 111 def postorder(self): 112 """后序遍历递归版本 113 遍历顺序为left->right->root 114 115 :returns: 116 :rtype: 117 118 """ 119 120 if not self: 121 return 122 123 if self.left: 124 for x in self.left.postorder(): 125 yield x 126 127 if self.right: 128 for x in self.right.postorder(): 129 yield x 130 131 yield self 132 133 def postorder_norecur(self): 134 """后序遍历非递归版本 135 遍历顺序为left->right->root 136 和中序遍历不同的是,只有下面两种情况之一才能出栈: 137 1. 栈顶元素为叶子节点,此时肯定可以出栈,否则没有节点可以入栈了 138 2. 栈顶元素不是叶子节点,但是上一个出栈的元素是栈顶元素的右子节点 139 上一个出栈的元素是栈顶元素的右子节点说明节点的右子数已经遍历过了, 140 所以现在当前节点可以出栈了 141 142 :returns: 143 :rtype: 144 145 """ 146 147 if not self: 148 return 149 150 stack = [] 151 152 node = self 153 last_node = None 154 while node is not None or len(stack) > 0: 155 if node is not None: 156 stack.append(node) 157 node = node.left 158 else: 159 # 这里不会越界,因为能进到这里的前提条件是node is None 160 # 这时必然有stack非空,否则while循环就退出了 161 temp = stack[-1] 162 if temp.is_leaf or temp.right is last_node: 163 node = stack.pop() 164 last_node = node 165 yield node 166 # 这里node要设置为None,因为该节点及左右子树都已遍历,需要向上回溯了 167 # 注意中序遍历时这里设置的是node=node.right,因为右子树实在父节点 168 # 遍历后才遍历的 169 node = None 170 else: 171 node = temp.right 172 173 def breadth_frist(self): 174 """广度优先遍历 175 和深度优先遍历(前/中/后序遍历)的区别是使用队列而不是栈. 176 :returns: 177 :rtype: 178 179 """ 180 181 if not self: 182 return 183 184 queue = [self] 185 while queue: 186 node = queue.pop(0) # 弹出队列首个元素,若直接调用list.pop()则弹出末尾元素 187 yield node 188 if node.left: 189 queue.append(node.left) 190 if node.right: 191 queue.append(node.right) 192 193 194 @property 195 def children(self): 196 """ 197 Returns an iterator for the non-empty children of the Node 198 199 The children are returned as (Node, pos) tuples where pos is 0 for the 200 left subnode and 1 for the right. 201 202 >>> len(list(create(dimensions=2).children)) 203 0 204 205 >>> len(list(create([ (1, 2) ]).children)) 206 0 207 208 >>> len(list(create([ (2, 2), (2, 1), (2, 3) ]).children)) 209 2 210 """ 211 212 if self.left and self.left.data is not None: 213 yield self.left, 0 214 if self.right and self.right.data is not None: 215 yield self.right, 1 216 217 def set_child(self, index, child): 218 """ Sets one of the node‘s children 219 220 index 0 refers to the left, 1 to the right child """ 221 222 if index == 0: 223 self.left = child 224 else: 225 self.right = child 226 227 def height(self): 228 229 min_height = int(bool(self)) 230 return max([min_height] + [c.height() + 1 for c, p in self.children]) 231 232 def __repr__(self): 233 return ‘<%(cls)s - %(data)s>‘ % 234 dict(cls=self.__class__.__name__, data=repr(self.data)) 235 236 # def __nonzero__(self): 237 # return self.data is not None 238 239 # __bool__ = __nonzero__ 240 241 # def __eq__(self, other): 242 # if isinstance(other, tuple): 243 # return self.data == other 244 # else: 245 # return self.data == other.data 246 247 def __hash__(self): 248 return id(self)
kd_tree.py:KD树
1 # -*- coding: utf-8 -*- 2 3 import numpy as np 4 from collections import deque 5 from scipy.spatial.distance import euclidean 6 from tree import Node 7 8 9 class KDNode(Node): 10 def __init__(self, 11 data=None, 12 left=None, 13 right=None, 14 axis=None): 15 super(KDNode, self).__init__(data, left, right) 16 self.axis = axis 17 18 19 class KDTree: 20 """ 21 KD树的实现。 22 注意树结构中,输入数据会被原样保存在points成员中,node.data存储的是数据在points中的位置 23 索引,相当于保存了指针。 24 """ 25 def __init__(self, dimension, dist_func=euclidean, leaf_size=5): 26 """初始化 27 28 :param dimension: 29 :param dist_func: 30 :param leaf_size: 31 :returns: 32 :rtype: 33 34 """ 35 self.dimension = dimension 36 self.root = None 37 self.dist_func = dist_func 38 self.leaf_size = leaf_size 39 40 def _next_axis(self, current_axis): 41 return (current_axis + 1) % self.dimension 42 43 def _create(self, handles, current_axis): 44 if len(handles) <= self.leaf_size: 45 return KDNode(handles, None, None, None) 46 ## handle排序要用到真实的数据 47 handles.sort(key=lambda x: self.points[x][current_axis]) 48 median = len(handles) // 2 49 data = [handles[median]] # 数据点是list格式,存储handle 50 left = self._create(handles[:median], self._next_axis(current_axis)) 51 right = self._create(handles[median + 1:], 52 self._next_axis(current_axis)) 53 54 return KDNode(data, left, right, axis=current_axis) 55 56 def __getitem__(self,key): 57 return self.points[key] 58 59 def height(self): 60 if self.root: 61 return self.root.height() 62 else: 63 raise ValueError("KD树尚未构建") 64 65 66 67 def create(self, points): 68 self.points=points 69 handles=list(range(len(points))) 70 self.root = self._create(handles, 0) 71 self.maxes = np.amax(self.points,axis=0) 72 self.mins = np.amin(self.points,axis=0) 73 74 75 def router(self, root, point): 76 """给定一个点,找到它属于的叶子节点,返回从root到叶子节点路径上的所有节点 77 78 :param root: 根节点 79 :param point: 指定点 80 :returns: 81 :rtype: 82 83 """ 84 results = [root] 85 node = root 86 while not node.is_leaf: 87 if point[node.axis] < self.points[node.data[0]][node.axis]: 88 node = node.left 89 else: 90 node = node.right 91 results.append(node) 92 return results 93 94 def find_nn(self, node, point, k): 95 """计算node数据中与point最近的k个点 96 这里采用的方式是逐个计算然后排序,比较慢 97 :param node: KD树的某个节点 98 :param point: 待比较数据点 99 :param k: 100 :returns: 101 :rtype: 102 103 """ 104 dists = [self.dist_func(self.points[x], point) for x in node.data] 105 idx = np.argsort(dists)[:k] 106 # return [(dists[i],self.points[node.data[i]]) for i in idx] 107 return [(dists[i],node.data[i]) for i in idx] 108 109 def check_intersection(self, node, point, radius): 110 """检查node对应的的切分超平面是否与(point,radius)定义的超球体相交 111 NOTE:如果不是欧式距离,会不会对相交的判断有影响? 112 113 :param node: KD树的某个节点 114 :param point: 球心 115 :param radius: 球半径 116 :returns: 117 :rtype: 118 119 """ 120 if node.is_leaf: 121 raise ValueError("节点不能是叶子节点!") 122 point_2 = point.copy() 123 point_2[node.axis] = self.points[node.data[0]][node.axis] 124 dist = self.dist_func(point, point_2) 125 return True if dist < radius else False 126 127 def knn(self, point, k=1, verbose=True): 128 """利用kd树寻找knn 129 实现方法有点类似树的后序遍历,区别在于这里有些子节点不需要遍历,而且遍历顺序是不固定的. 130 对每个访问过的节点都标记成已访问 131 132 :param point: 输入数据点 133 :param k: 返回最近邻的数据 134 :param verbose: 为True表示会输出详细处理信息 135 :returns: k近邻搜索结果,注意返回的是数据在kd树中的id而非数据点本身 136 :rtype: list of tuple(distance,point_id) 137 138 """ 139 140 if verbose: 141 vprint = print 142 else: 143 vprint = lambda x: None 144 if not self.root: 145 raise ValueError("KD树尚未构建...") 146 # 初始化 147 for node in self.root.preorder_norecur(): 148 node.visited = None 149 vistied_points = 0 150 # results = [(None, -np.inf)] * k 151 results = [(np.inf, None)] * k 152 ## 也可以用堆来实现nn的更新 153 # heapq.heapify(results) 154 vprint("初始化节点栈为树根节点") 155 path = self.router(self.root,point) 156 while path: 157 node = path.pop() 158 node.visited = True 159 vistied_points += len(node.data) 160 vprint("{}更新结果集".format(" " * 4)) 161 neighbors=self.find_nn(node, point, k) 162 results.extend(neighbors) 163 results.sort(key=lambda x: x[0]) 164 results = results[:k] 165 166 # for neighbor in neighbors: 167 # heapq.heappushpop(results,neighbor) 168 169 if len(path) == 0: 170 vprint("搜索结束,一共搜索了{}个数据点".format(vistied_points)) 171 return results 172 # sorted_results = heapq.nlargest(k,results) 173 # return [(x[0],x[1]) for x in sorted_results] 174 parent = path[-1] 175 vprint("{}判断节点的切分平面是否与超球体相交".format(" " * 4)) 176 # radius = results[-1][1] 177 radius = results[-1][0] 178 if self.check_intersection(parent, point, radius): 179 vprint("{}相交,另一个子节点加入处理栈".format(" " * 8)) 180 other_node = parent.left if parent.right is node else parent.right 181 # 如果没访问过,就访问,否则回溯到父节点 182 if not other_node.visited: 183 path.extend(self.router(other_node,point)) 184 vprint("剩余节点数:{}".format(len(path))) 185 186 187 188 def _min_dist(self,maxes,mins,point): 189 return self.dist_func(point*0, np.maximum(0,np.maximum(mins-point,point-maxes))) 190 191 def _max_dist(self,maxes,mins,point): 192 return self.dist_func(point*0, np.maximum(maxes-point,point-mins)) 193 194 ## 寻找距离点x小于r的所有点 195 def query_ball_point(self, point, r): 196 stack=[(self.root,self.maxes,self.mins)] 197 results=[] 198 while stack: 199 node,maxes,mins=stack.pop() 200 # 如果是叶子节点,检查节点保存的数据是否满足即可 201 if node.is_leaf: 202 for handle in node.data: 203 distance=self.dist_func(self.points[handle],point) 204 if distance<=r: 205 results.append((distance,handle)) 206 207 # 如果矩形内所有点距离都大于r,不用检查 208 elif self._min_dist(maxes,mins,point) > r: 209 continue 210 211 # 如果矩形内所有点距离都小于r,遍历,把所有节点都返回 212 elif self._max_dist(maxes,mins,point) < r : 213 for sub_node in node.preorder_norecur(): 214 for handle in sub_node.data: 215 distance=self.dist_func(self.points[handle],point) 216 results.append((distance,handle)) 217 218 # 如果都不满足,拆成子矩形,继续检查 219 else: 220 # 先判断将当前节点的数据是否满足条件 221 handle = node.data[0] 222 distance=self.dist_func(self.points[handle],point) 223 if distance<=r: 224 results.append((distance,handle)) 225 226 # 改变左子节点的最大值和右子节点的最小值 227 left_maxes=maxes.copy() 228 left_maxes[node.axis]=self.points[node.data[0]][node.axis] 229 230 right_mins=mins.copy() 231 right_mins[node.axis]=self.points[node.data[0]][node.axis] 232 233 # 入栈 234 stack.append((node.left,left_maxes,mins)) 235 stack.append((node.right,maxes,right_mins)) 236 results.sort(key=lambda x:x[0] ) 237 return results 238 239 if __name__=="__main__": 240 241 def knn_direct(points, point, k, dist_func=euclidean): 242 dists = [dist_func(x, point) for x in points] 243 idx = np.argsort(dists)[:k] 244 return [( dists[i],i) for i in idx] 245 246 def query_ball_point_direct(points, input_point, r, dist_func=euclidean): 247 results=[] 248 for ii in range(len(points)): 249 distance=dist_func(points[ii],input_point) 250 if distance<=r: 251 results.append((distance,ii)) 252 results.sort(key=lambda x:x[0] ) 253 return results 254 255 256 ##### test ##### 257 258 259 def test_knn(dim=3, point_num=5000, k=10, verbose=False): 260 261 points = [np.random.rand(dim) for ii in range(point_num)] 262 263 input_point = np.random.rand(dim) 264 265 kd_tree = KDTree(dimension=dim,leaf_size=10) 266 kd_tree.create(points) 267 268 269 kd_tree_result = kd_tree.knn(input_point, k, verbose=verbose) 270 kd_tree_result_points=[kd_tree[x[1]] for x in kd_tree_result] 271 kd_tree_result_distance = [x[0] for x in kd_tree_result] 272 273 direct_result=knn_direct(points, input_point, k, dist_func=euclidean) 274 direct_result_points=[points[x[1]] for x in direct_result] 275 direct_result_distance = [x[0] for x in direct_result] 276 277 distance_result = np.array_equal(kd_tree_result_distance, direct_result_distance) 278 points_result = np.array_equal(kd_tree_result_points, direct_result_points) 279 if not distance_result : 280 print("距离计算错误!") 281 elif not points_result: 282 print("数据点计算错误!") 283 else: 284 print("测试通过!!!!!") 285 286 def test_query(dim=3, point_num=5000, r=0.2, verbose=False): 287 288 points = [np.random.rand(dim) for ii in range(point_num)] 289 290 input_point = np.random.rand(dim) 291 292 kd_tree = KDTree(dimension=dim,leaf_size=10) 293 kd_tree.create(points) 294 295 296 kd_tree_result=kd_tree.query_ball_point(input_point,r) 297 kd_tree_result_points=[kd_tree[x[1]] for x in kd_tree_result] 298 kd_tree_result_distance = [x[0] for x in kd_tree_result] 299 300 direct_result = query_ball_point_direct(points, input_point, r, dist_func=euclidean) 301 direct_result_points=[points[x[1]] for x in direct_result] 302 direct_result_distance = [x[0] for x in direct_result] 303 304 distance_result = np.array_equal(kd_tree_result_distance, direct_result_distance) 305 points_result = np.array_equal(kd_tree_result_points, direct_result_points) 306 if not distance_result : 307 print("距离计算错误!") 308 elif not points_result: 309 print("数据点计算错误!") 310 else: 311 print("测试通过!!") 312 313 314 def test_traversal(dim=3, point_num=20, traversal_type="postorder"): 315 if traversal_type not in ["preorder", "inorder", "postorder"]: 316 raise ValueError( 317 "traversal_type "{}" not recognized".format(traversal_type)) 318 319 points = [np.random.rand(dim) for ii in range(point_num)] 320 321 kd_tree = KDTree(dimension=dim) 322 kd_tree.create(points) 323 324 if traversal_type == "preorder": 325 traversal_iter = zip(kd_tree.root.preorder(), 326 kd_tree.root.preorder_norecur()) 327 elif traversal_type == "inorder": 328 traversal_iter = zip(kd_tree.root.inorder(), 329 kd_tree.root.inorder_norecur()) 330 elif traversal_type == "postorder": 331 traversal_iter = zip(kd_tree.root.postorder(), 332 kd_tree.root.postorder_norecur()) 333 334 for ii, jj in traversal_iter: 335 if ii is jj: 336 print("OK") 337 else: 338 print("BAD")
heap.py:最小堆
1 # -*- coding: utf-8 -*- 2 3 from verbose import Verbose 4 5 class Heap(Verbose): 6 """ 7 最小堆,同时可直接用作优先队列 8 9 """ 10 11 def __init__(self, verbose=True): 12 """初始化 13 heap成员存储的元素是[key,handle]形式的list 14 handle_dict存放handle和heap位置的对应关系,用于快速检索元素在heap中的下标 15 具体的数据可以存放在外部,只要与handle_dict的key一一对应即可 16 :returns: 17 :rtype: 18 19 """ 20 self.heap = [] # 21 self.handle_dict = {} # 22 super(Heap, self).__init__(verbose) 23 24 def _siftup(self, pos): 25 """维护最小堆结构,即算法导论中的max-heapify函数 26 思路: 27 假设pos的左右子节点均已经是最小堆,但是pos位置的值可能大于其左右子节点值, 28 所以要找到更小的子节点(childpos),然后交换根节点(pos)和最小子节点的值。 29 这样以来,对应子节点的最小堆性质可能会被破坏,所以要在子节点上执行同样的操 30 作,这样一直递归地走下去直到达到叶子节点。 31 时间复杂度为O(logN) 32 :param pos: 33 :returns: 34 :rtype: 35 36 """ 37 38 end_pos = len(self.heap) 39 lchild = 2 * pos + 1 40 rchild = lchild + 1 41 42 # 最小节点设置为左子节点 43 min_pos = lchild 44 # 若左子节点都不小于end_pos,说明pos肯定是叶子节点了 45 while min_pos < end_pos: 46 if self.heap[min_pos] > self.heap[pos]: 47 min_pos = pos 48 if rchild < end_pos and self.heap[min_pos] > self.heap[rchild]: 49 min_pos = rchild 50 if min_pos != pos: 51 ## 不满足最小堆性质,进行交换 52 self.printer("交换位置{}:{}和{}:{}的数据".format( 53 min_pos, self.heap[min_pos], pos, self.heap[pos])) 54 self.printer("交换位置{}和{}的数据".format(min_pos, pos)) 55 self.heap[min_pos], self.heap[pos] = self.heap[pos], self.heap[ 56 min_pos] 57 self.printer("更新handle_dict") 58 self.printer("{}->{}".format(self.heap[pos][1], min_pos)) 59 self.printer("{}->{}".format(self.heap[min_pos][1], pos)) 60 self.handle_dict[self.heap[pos][1]] = pos 61 self.handle_dict[self.heap[min_pos][1]] = min_pos 62 pos = min_pos 63 lchild = 2 * pos + 1 64 rchild = lchild + 1 65 min_pos = lchild 66 else: 67 # 满足最小堆性质,不用处理 68 break 69 70 def _siftdown(self, pos): 71 """当一个节点(pos)值变小时,为了保持最小堆性质,需要将该值往上浮动, 72 具体做法就是不断交换节点值和父节点值,类似冒泡排序。 73 注意: 74 1. 减小节点的值不会影响子节点的最小堆性质 75 2. 交换该节点和其父节点的值也不会影响该节点的子节点的最小堆性质,因为 76 父节点的值肯定小于该节点的两个子节点 77 时间复杂度为O(logN) 78 :param startpos: 79 :param pos: 80 :returns: 81 :rtype: 82 83 """ 84 new_item = self.heap[pos] 85 while pos > 0: 86 parentpos = (pos - 1) >> 1 87 parent_item = self.heap[parentpos] 88 # 如果当前节点值小于父节点值,上浮 89 if new_item < parent_item: # list之间的比较是比较其第一个元素,即key 90 self.heap[pos] = parent_item 91 self.handle_dict[parent_item[1]] = pos # 更新handle_dict位置信息 92 pos = parentpos 93 continue 94 # 一旦发现不小于了,就结束,把原来pos位置的值(new_item)放在这里 95 break 96 self.heap[pos] = new_item 97 self.handle_dict[new_item[1]] = pos 98 99 def heapify(self, x): 100 """建堆 101 时间复杂度为O(N) 102 :param x: [list] 输入数据,格式为[[key,handle]..] 103 :returns: 104 :rtype: 105 106 """ 107 n = len(x) 108 self.heap = x 109 for i in range(n): 110 self.handle_dict[x[i][1]] = i 111 ## 只有前半部分数据才能成为根节点 112 for i in reversed(range(n // 2)): 113 self._siftup(i) 114 115 def push(self, data): 116 """添加一个元素 117 时间复杂度为O(logN) 118 :param data: 119 :returns: 120 :rtype: 121 122 """ 123 key, handle = data 124 try: 125 # 已经存在,增加或者减小key 126 pos = self.handle_dict[handle] 127 if self.heap[pos][0] > key: 128 self.decrease_key(data) 129 elif self.heap[pos][0] < key: 130 self.increase_key(data) 131 except: 132 # 不存在,添加之,具体做法是将元素添加到heap的最后面,作为叶子节点 133 # 然后逐渐上浮 134 self.heap.append(data) 135 self.handle_dict[handle] = len(self.heap) - 1 136 self._siftdown(len(self.heap) - 1) 137 138 def decrease_key(self, data): 139 """减小某个元素的key 140 减小key时,当前节点及子节点的最小堆性质肯定会留存,所以不需要再维护最小堆 141 性质,只需要当前元素往上浮即可 142 时间复杂度为O(logN) 143 :param data: 144 :returns: 145 :rtype: 146 147 """ 148 new_key, handle = data 149 pos = self.handle_dict[handle] 150 if self.heap[pos][0] < new_key: 151 raise ValueError("新的key比原有key更大") 152 self.heap[pos][0] = new_key 153 self._siftdown(pos) 154 155 def increase_key(self, data): 156 """增加某个元素的key,和decrease_key类似 157 时间复杂度为O(logN) 158 :param data: 159 :returns: 160 :rtype: 161 162 """ 163 new_key, handle = data 164 pos = self.handle_dict[handle] 165 if self.heap[pos][0] > new_key: 166 raise ValueError("新的key比原有key更小") 167 self.heap[pos][0] = new_key 168 self._siftup(pos) 169 170 def pop(self): 171 """弹出最小元素,保持小堆性质不变。 172 具体方法如下(假设堆非空): 173 1. 弹出heap最后一个元素(last_item) 174 2. 返回值设置为第一个元素(最小值) 175 3. heap第一个元素设置为last_item 176 4. 在第一个元素的位置上执行_siftup 177 以上步骤可以避免直接弹出heap第一个元素后又要把最后一个元素移至首位的麻烦 178 该方法也可以直接用于堆排序,但是要注意数据备份 179 :returns: 180 :rtype: 181 182 """ 183 last_item = self.heap.pop() 184 if self.heap: 185 return_item = self.heap[0] 186 self.heap[0] = last_item 187 188 ## 更新handle_dict 189 self.handle_dict[last_item[1]] = 0 190 del self.handle_dict[return_item[1]] 191 self._siftup(0) 192 else: 193 return_item = last_item 194 del self.handle_dict[return_item[1]] 195 return return_item 196 197 def min(self): 198 """返回堆的最小值 199 时间复杂度为O(1) 200 :returns: 堆中的最小元素 201 :rtype: list 202 203 """ 204 return self.heap[0] 205 206 @property 207 def is_empty(self): 208 return True if len(self.heap) == 0 else False 209 210 211 if __name__=="__main__": 212 import numpy as np 213 def build_heap(data_size): 214 indices = list(range(data_size)) 215 keys = np.random.rand(data_size) 216 handles = list(range(data_size)) 217 np.random.shuffle(handles) 218 data = [list(x) for x in zip(keys, handles)] 219 np.random.shuffle(indices) 220 data = [data[idx] for idx in indices] 221 zzs = Heap(verbose=False) 222 zzs.heapify(data) 223 return zzs 224 225 226 def do_test(heap): 227 data_size = len(heap.heap) 228 229 reason = "通过!" 230 for pos in range(data_size // 2): 231 lchild = pos * 2 + 1 232 rchild = lchild + 1 233 if lchild < data_size and heap.heap[lchild] < heap.heap[pos]: 234 reason = "失败:左子节点更小" 235 break 236 if rchild < data_size and heap.heap[rchild] < heap.heap[pos]: 237 reason = "失败:右子节点更小" 238 break 239 for handle in heap.handle_dict: 240 pos = heap.handle_dict[handle] 241 if heap.heap[pos][1] != handle: 242 reason = "建堆测试通过,但handle_dict记录不正确" 243 break 244 print(reason) 245 246 247 def test_heapify(data_size=10): 248 """测试建堆函数,同时也测试了_siftup函数 249 250 :param data_size: 251 :returns: 252 :rtype: 253 254 """ 255 zzs = build_heap(data_size) 256 do_test(zzs) 257 258 259 def test_siftdown(data_size=10): 260 zzs=build_heap(data_size) 261 pos=np.random.randint(data_size) 262 zzs._siftdown(pos) 263 ## 测试堆的性质是否能够保留 264 print("测试1:不改变数据,直接调用") 265 do_test(zzs) 266 267 print("测试2:减小节点数据后再调用") 268 zzs.heap[pos][0]=-np.inf 269 zzs._siftdown(pos) 270 do_test(zzs) 271 272 def test_decrease_key(data_size=10): 273 zzs=build_heap(data_size) 274 pos=np.random.randint(data_size) 275 zzs.decrease_key([-np.inf,pos]) 276 do_test(zzs) 277 278 def test_increase_key(data_size=10): 279 zzs=build_heap(data_size) 280 pos=np.random.randint(data_size) 281 zzs.increase_key([np.inf,pos]) 282 do_test(zzs) 283 284 def test_push(data_size=10): 285 zzs=build_heap(data_size) 286 print("测试1:插入重名节点,值更小") 287 pos=np.random.randint(data_size) 288 new_data=zzs.heap[pos].copy() 289 new_data[0]=new_data[0]-1 290 zzs.push(new_data) 291 do_test(zzs) 292 print("测试2:插入重名节点,值更大") 293 pos=np.random.randint(data_size) 294 new_data=zzs.heap[pos].copy() 295 new_data[0]=new_data[0]+1 296 zzs.push(new_data) 297 do_test(zzs) 298 print("测试3:插入重名节点,值不变") 299 pos=np.random.randint(data_size) 300 new_data=zzs.heap[pos].copy() 301 zzs.push(new_data) 302 do_test(zzs) 303 print("测试4:插入新节点") 304 new_data=[np.inf,data_size] 305 zzs.push(new_data) 306 do_test(zzs) 307 308 def test_pop(data_size=10): 309 zzs=build_heap(data_size) 310 pop_result=[] 311 while zzs.heap: 312 pop_result.append(zzs.pop()) 313 try: 314 do_test(zzs) 315 except: 316 continue 317 pop_result=[x[0] for x in pop_result] 318 print(pop_result) 319
optics.py:optics算法主程序
1 # -*- coding: utf-8 -*- 2 3 import itertools 4 import numpy as np 5 from functools import reduce 6 from itertools import count 7 from matplotlib import pyplot as plt 8 from scipy.spatial.distance import euclidean 9 from collections import defaultdict, OrderedDict 10 from sklearn.cluster import DBSCAN 11 from sklearn import datasets 12 from matplotlib.pyplot import cm 13 14 from kd_tree import KDTree 15 from heap import Heap 16 from verbose import Verbose 17 class OPTICS(Verbose): 18 def __init__(self, 19 max_eps=0.5, 20 min_samples=10, 21 metric=euclidean, 22 verbose=True): 23 self.max_eps = max_eps 24 self.min_samples = min_samples 25 self.metric = metric 26 super(OPTICS, self).__init__(verbose) 27 28 def _get_neighbors(self, point_id): 29 """计算数据点的eps-邻域,同时也得到core-distance 30 :param point_id: 31 :returns: 32 :rtype: 33 34 """ 35 point = self.kd_tree[point_id] 36 neighbors = self.kd_tree.query_ball_point(point, self.max_eps) 37 ## 把节点本身排除在外 38 neighbors.pop(0) 39 40 if len(neighbors) < self.min_samples: 41 core_distance = np.inf 42 else: 43 core_distance = neighbors[self.min_samples - 1][0] 44 45 return [x[1] for x in neighbors], core_distance 46 47 def _update(self, order_seeds, neighbors, point_id): 48 """ 49 50 :returns: 51 :rtype: 52 """ 53 ## 能进到这个函数的core_distance都是满足core_distance<np.inf的 54 core_distance = self.results[point_id][1] 55 for neighbor in neighbors: 56 ## 如果该邻域点没有处理过,更新reachability_distance 57 ## 注意:如果某个点已经处理过(计算core_distance并作为point_id进入该函数),那么 58 ## 该点的reachability_distance就不会再被更新了,即采用“先到先得”的模式 59 if not self.results[neighbor][0]: 60 self.printer("节点{}尚未处理,计算可达距离".format(neighbor)) 61 new_reachability_distance = max(core_distance, 62 self.metric( 63 self.kd_tree[point_id], 64 self.kd_tree[neighbor])) 65 66 ## 如果新的reachability_distance小于老的,那么进行更新,否则不更新 67 if new_reachability_distance < self.results[neighbor][2]: 68 self.printer("节点{}的可达距离从{}缩短至{}".format( 69 neighbor, self.results[neighbor][2], 70 new_reachability_distance)) 71 self.results[neighbor][2] = new_reachability_distance 72 ## 对新数据执行插入,对老数据执行decrease_key 73 order_seeds.push([new_reachability_distance, neighbor]) 74 75 def _expand_cluste_order(self, point_id): 76 """FIXME! briefly describe function 77 78 79 :param point_id: 80 :returns: 81 :rtype: 82 83 """ 84 85 neighbors, core_distance = self._get_neighbors(point_id) 86 self.printer("节点{}的邻域点数量为{},核心距离为{}".format(point_id, len(neighbors), 87 core_distance)) 88 self.results[point_id][0] = True # 标记为已处理 89 self.results[point_id][1] = core_distance 90 self.results_order.append(point_id) # 记录数据点被处理的顺序 91 if core_distance < np.inf: 92 self.printer("节点{}为核心点,递归处理其邻域".format(point_id)) 93 ## order_seeds是以reachability_distance为key,point_id为handle的优先队列(堆) 94 order_seeds = Heap(verbose=False) 95 data = [[self.results[x][2], x] for x in neighbors] 96 order_seeds.heapify(data) 97 self._update(order_seeds, neighbors, point_id) 98 while not order_seeds.is_empty: 99 _, current_point_id = order_seeds.pop() 100 neighbors, core_distance = self._get_neighbors( 101 current_point_id) 102 self.printer("节点{}的邻域点数量为{},核心距离为{}".format( 103 current_point_id, len(neighbors), core_distance)) 104 self.results[current_point_id][0] = True # 标记为已处理 105 self.results[current_point_id][1] = core_distance 106 self.results_order.append(current_point_id) 107 if core_distance < np.inf: 108 self.printer("节点{}为核心点,递归处理其邻域".format(point_id)) 109 self._update(order_seeds, neighbors, current_point_id) 110 111 def fit(self, points): 112 """聚类主函数 113 聚类过程主要是通过expand_cluste_order函数实现,流程如下: 114 给定一个起始点pt,计算pt的core_distance和eps-邻域,并更新eps-邻域中数据点的 115 reachability_distance 116 然后按reachability_distance从小到大依次处理pt的eps-邻域中未处理的点(流程同上) 117 118 遍历整个数据集,对每个未expand的数据点都执行expand,便完成了聚类,结果存储在self.results中 119 数据点遍历顺序存储在self.results_order中,二者结合便可以导出具体的聚类信息 120 121 :param points: [list] 输入数据列表,list中的每个元素都是长度固定的1维np数组 122 :returns: 123 :rtype: 124 125 """ 126 127 self.point_num = len(points) 128 self.point_size = points[0].size 129 self.results = [[None, np.inf, np.inf] for x in range(self.point_num)] 130 self.results_order = [] 131 ## 数据存储在kd树中以便检索【好像并没有用到检索...】 132 self.kd_tree = KDTree(self.point_size) 133 self.kd_tree.create(points) 134 135 for point_id in range(self.point_num): 136 ## 如果当前节点没有处理过,执行expand 137 if not self.results[point_id][0]: 138 self._expand_cluste_order(point_id) 139 return self 140 141 def extract(self, eps): 142 """从计算结果中抽取出聚类信息 143 抽取的方式比较简单,就是扫描所有数据点,判断当前点的core_distance 144 和reachability_distance与给定eps的大小,然后决定点的类别。规则如下: 145 1. 如果reachability_distance<eps,属于当前类别 146 2. 如果大于eps,不属于当前类别 147 2-1. 如果core_distance小于eps,可以自成一类 148 2-2. 如果core_distance大于eps,认为是噪声点 149 注意: 150 数据的扫描顺序同fit函数中的处理顺序是一致的。 151 :returns: 152 :rtype: 153 154 """ 155 if eps > self.max_eps: 156 raise ValueError("eps参数不能大于{},当前值为{}".format(self.max_eps, eps)) 157 labels = np.zeros(self.point_num, dtype=np.int64) 158 counter = count() 159 idx = next(counter) 160 for point_id in self.results_order: 161 # for point_id in range(self.point_num): 162 _, core_distance, reachability_distance = self.results[point_id] 163 ## 如果可达距离大于eps,认为要么是core point要么是噪音数据 164 if reachability_distance > eps: 165 ## 如果core distance小于eps,那么可以成为一个类 166 if core_distance < eps: 167 idx = next(counter) 168 labels[point_id] = idx 169 ## 否则成为噪声数据 170 else: 171 labels[point_id] = 0 172 ## 可达距离小于eps,属于当前类别 173 ## 这个点的顺序是由fit函数中的主循环函数维持的,注意 174 else: 175 labels[point_id] = idx 176 177 return labels 178 179 180 def extract_postprocess(labels): 181 clusters = defaultdict(list) 182 for ii in range(len(labels)): 183 idx = str(labels[ii]) 184 clusters[idx].append(ii) 185 return clusters 186 187 188 ############################################################### 189 if __name__ == "__main__": 190 191 def generate_test_data(n_samples=1000): 192 """生成测试数据 193 194 :param n_samples: 195 :returns: 196 :rtype: 197 198 """ 199 # varied 200 data = datasets.make_blobs( 201 n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5]) 202 203 # # noisy_circles 204 # data = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05) 205 206 # # noisy_moons 207 # data = datasets.make_moons(n_samples=n_samples, noise=.05) 208 209 # # blob 210 # data = datasets.make_blobs(n_samples=n_samples, random_state=8) 211 212 return data 213 214 def hierarchical_dataset(): 215 cluster_1 = [3 * np.random.rand(2) for x in range(100)] 216 cluster_2 = [0.5 + np.random.rand(2) / 1.2 for x in range(200)] 217 cluster_3 = [0.5 + np.random.rand(2) / 4 for x in range(200)] 218 cluster_4 = [2 + np.random.rand(2) / 3 for x in range(100)] 219 cluster_5 = [ 220 np.array([0, 5]) + np.random.rand(2) * 1.3 for x in range(100) 221 ] 222 cluster_6 = [5 + np.random.randn(2) / 5 for x in range(200)] 223 cluster_7 = [5 + np.random.randn(2) for x in range(100)] 224 data = cluster_1 + cluster_2 + cluster_3 + cluster_4 + cluster_5 + cluster_6 + cluster_7 225 return data 226 227 def scatter(data, labels=None): 228 """画散点图 229 230 :param data: [list|np.array] 1维np数组构成的列表或两维np数组,第1和第2列分别表示横纵坐标 231 :param label: [list|np.array|None] 数据点属于的类别,长度与data相同 232 :returns: 233 :rtype: 234 235 """ 236 data = np.array(data) 237 if labels is not None: 238 plt.scatter(data[:, 0], data[:, 1], c=np.array(labels)) 239 else: 240 plt.scatter(data[:, 0], data[:, 1]) 241 plt.show() 242 243 def test_optics(): 244 245 # data, _ = generate_test_data(10000) 246 # data = [data[i, :] for i in range(data.shape[0])] 247 248 data = hierarchical_dataset() 249 optics = OPTICS( 250 max_eps=20, min_samples=10, metric=euclidean, 251 verbose=False).fit(data) 252 253 ## 从结果中提取出reachability_distance,按照数据处理顺序排列 254 255 reachability_distance = np.array( 256 [optics.results[i][2] for i in optics.results_order]) 257 258 ## 从结果中生成一个聚类 259 260 eps = 1.1 261 optics_labels = optics.extract(eps) 262 263 color_nums = len(set(optics_labels)) 264 color_types = cm.rainbow(np.linspace(0, 1, color_nums)) 265 temp = [optics_labels[i] for i in optics.results_order] 266 colors = [color_types[i] for i in temp] 267 268 plot_data = np.array(data) 269 270 plt.subplot(1, 2, 1) 271 plt.scatter( 272 plot_data[:, 0], plot_data[:, 1], c=np.array(optics_labels)) 273 274 plt.subplot(1, 2, 2) 275 plt.bar( 276 np.arange(0, optics.point_num), 277 np.array(reachability_distance), 278 width=3, 279 color=colors) 280 plt.show() 281 282 def optics_vs_dbscan_2d(): 283 284 cluster_1 = [3 * np.random.rand(2) for x in range(100)] 285 cluster_2 = [0.5 + np.random.rand(2) / 1.2 for x in range(200)] 286 cluster_3 = [0.5 + np.random.rand(2) / 4 for x in range(200)] 287 cluster_4 = [2 + np.random.rand(2) / 3 for x in range(100)] 288 cluster_5 = [ 289 np.array([0, 5]) + np.random.rand(2) * 1.3 for x in range(100) 290 ] 291 cluster_6 = [5 + np.random.randn(2) / 5 for x in range(200)] 292 cluster_7 = [5 + np.random.randn(2) for x in range(100)] 293 294 cluster_2 = [3 + np.random.standard_exponential(2) for x in range(100)] 295 cluster_3 = [-3 + np.random.rand(2) for x in range(300)] 296 cluster_4 = [(-3 + np.random.rand(2)) * 3 for x in range(100)] 297 data = cluster_1 + cluster_2 + cluster_3 + cluster_4 298 # scatter(data) 299 300 ## OPTICS 301 optics = OPTICS( 302 max_eps=10, min_samples=10, metric=euclidean, 303 verbose=False).fit(data) 304 eps = 1 305 optics_labels = optics.extract(eps) 306 307 ## DBSCAN 308 array_data = np.array(data) 309 db = DBSCAN( 310 eps=eps, min_samples=10, metric=euclidean, 311 n_jobs=-1).fit(array_data) 312 313 db_labels = db.labels_ 314 315 ## plot 316 plt.subplot(1, 2, 1) 317 plt.scatter( 318 array_data[:, 0], array_data[:, 1], c=np.array(optics_labels)) 319 plt.title("OPTICS") 320 plt.subplot(1, 2, 2) 321 plt.scatter(array_data[:, 0], array_data[:, 1], c=np.array(db_labels)) 322 plt.title("DBSCAN") 323 plt.show()
运行optics.py文件中的test_optics函数,结果如下:
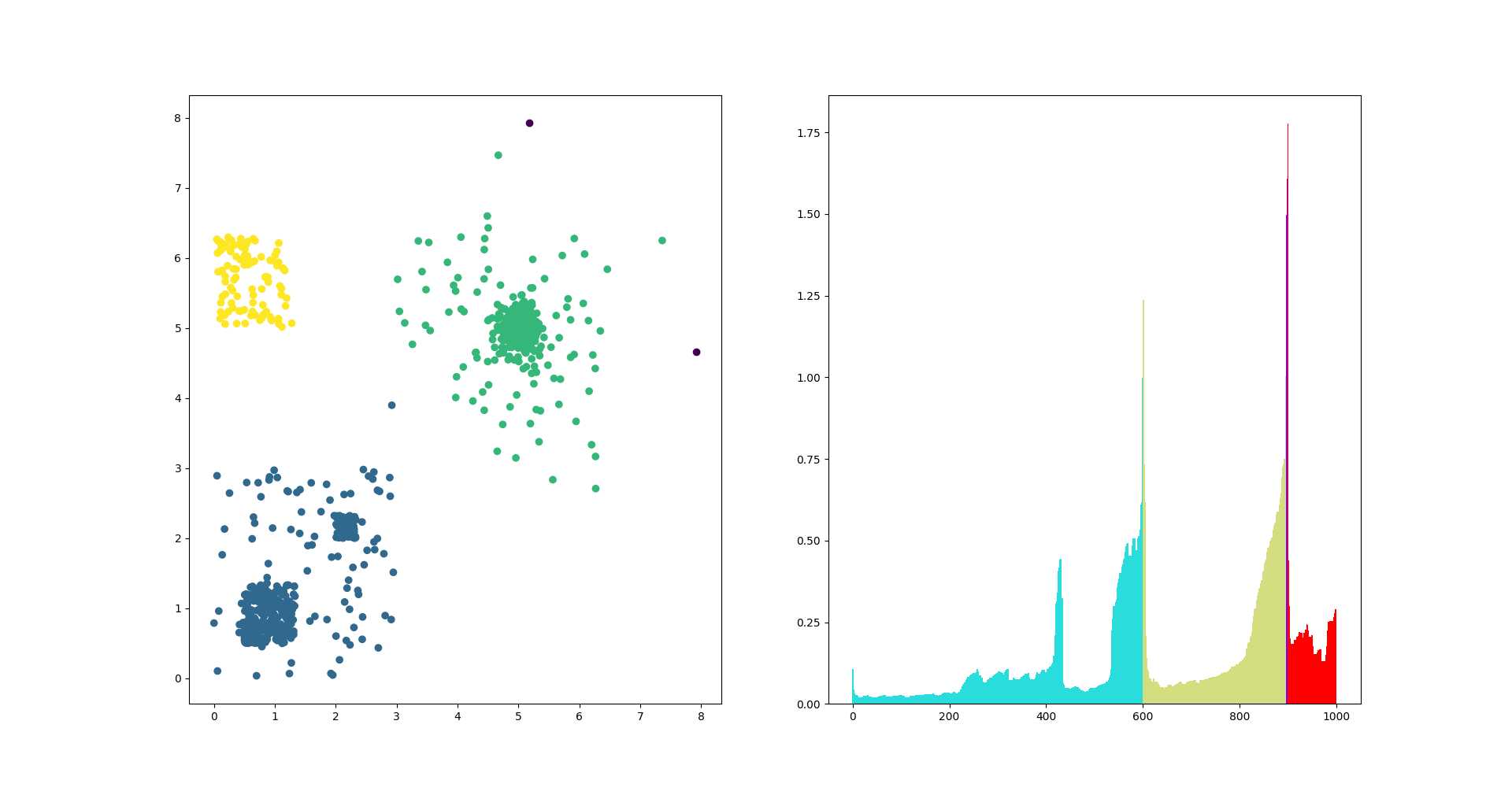
其中,左图是测试用数据点,不同颜色表示不同的聚类;右图是算法给出的distance排序(参见论文图9、图12),可见图中的凹陷的确与数据点的密度比较吻合,比如右图蓝色的类别,还可以按照密度再分为两个子类。
optics.py文件中的optics_vs_dbscan_2d函数是对同一组数据分别运行optics算法和dbscan算法,其结果如下:
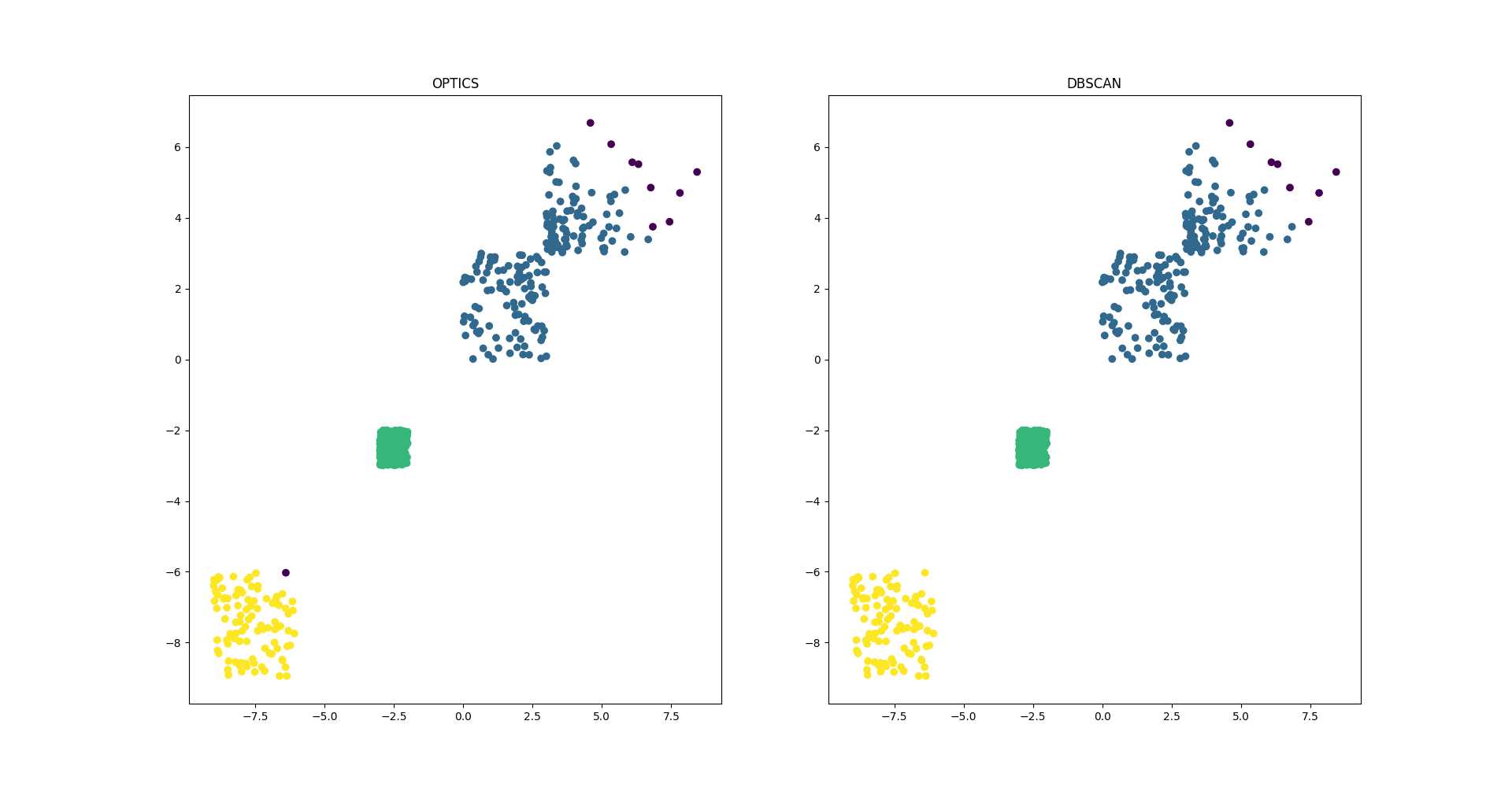
可见两个算法的计算结果只在一些边缘点上有差别,但是optics算法对初始参数非常不敏感,所以比dbscan要好用些。optics算法的缺点主要在于计算量更大,速度较慢。不过好在有高人提出了并行化的解决方案,下一篇再介绍。
以上是关于optics聚类算法的主要内容,如果未能解决你的问题,请参考以下文章