二分图的最小顶点覆盖 最大独立集 最大团

Posted 2021-01-12 1013star

二分图的最小顶点覆盖

定义：假如选了一个点就相当于覆盖了以它为端点的所有边。最小顶点覆盖就是选择最少的点来覆盖所有的边。

方法：最小顶点覆盖等于二分图的最大匹配。

我们用二分图来构造最小顶点覆盖。

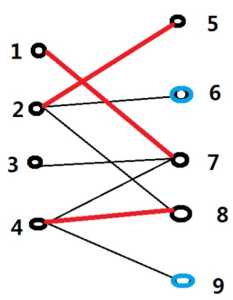
对于上面这个二分图，顶点分为左右两个集合，X集合包含1,2,3,4，Y集合包含5,6,7,8,9.假如现在我们已经找到一个最大匹配M，就是上面的红线所标注的M={(1,7),(2,5),(4,8)}。我们作如下定义：（1）定义1、2、4、5、7、8为已经匹配过的点，其他点为未匹配的点；（2）定义(4,8)、(1,7)、(2,5)为已匹配的边，其他边为未匹配的边。

下面我们从Y集合中找出未匹配的点，就是上面标记的6和9。每次我们从右边选出一个未匹配的点，从该点出发， 做一条未匹配边->匹配边->未匹配边->……->匹配边（注意最后以匹配边结尾），并且标记用到的点，得到下图：

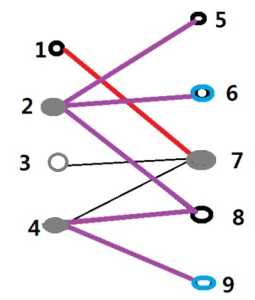
其中紫色的边为我们刚才画的边，其中标记的点有2、4、5、6、8、9。上图的两条路为：（1）9->4->8->2->5 （2）6->2->5。这两条路都是未匹配边->匹配边->未匹配边->……->匹配边。（注意如果一个右侧未匹配点有多条边，那么这样的从该点开始的路径就有多条，上面的6和9都只有一条边，所以从每个点开始的这样的路径只有一条）。

现在我们将左侧标记的点2、4和右侧未标记的点7选出组成集合S， 那个S就是一个最小顶点覆盖集，就是S集合可以覆盖所有的边。

二分图的最大独立集

定义：选出一些顶点使得这些顶点两两不相邻，则这些点构成的集合称为独立集。找出一个包含顶点数最多的独立集称为最大独立集。

方法：最大独立集=所有顶点数-最小顶点覆盖

 

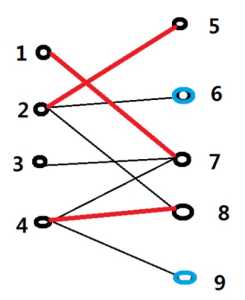
在上面这个图中最小顶点覆盖=3，即2,4,7构成最小顶点覆盖，则其他点6个构成最大独立集。且其他点不可能相连。假设其他点相连则这条边必定没有被2,4,7 覆盖，与2,4,7是最小顶点覆盖矛盾。因此其他点之间必定没有边。而2,4,7是最小顶点覆盖，所谓最小就是不能再小了，因此我们的独立集就是最大了。

二分图的最大团

定义：对于一般图来说，团是一个顶点集合，且由该顶点集合诱导的子图是一个完全图，简单说，就是选出一些顶点，这些顶点两两之间都有边。最大团就是使得选出的这个顶点集合最大。对于二分图来说，我们默认为左边的所有点之间都有边，右边的所有顶点之间都有边。那么，实际上，我们是要在左边找到一个顶点子集X，在右边找到一个顶点子集Y，使得X中每个顶点和Y中每个顶点之间都有边。

方法：二分图的最大团=补图的最大独立集。

补图的定义是：对于二分图中左边一点x和右边一点y，若x和y之间有边，那么在补图中没有，否则有。

这个方法很好理解，因为最大独立集是两两不相邻，所以最大独立集的补图两两相邻。