经典数值优化算法--专题学习

Posted 2021-01-12 melina-zh

通用的损失函数最优化的数值方法，来源于泰勒展开式，多元函数的泰勒展开式为：

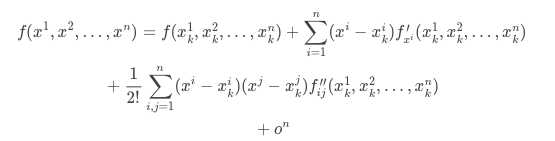
一、一阶逼近与一阶方法

一阶泰勒展开式：

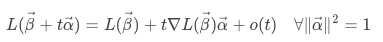
其中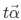，是代表了β变化的可能性，t在之后说到的梯度下降方法中演变成了学习速率。

现在，我们需要第二项最小，向量内积，最小为-|梯度||a|，这就是β的改变量。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！

于是，演变成了：

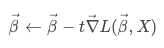
倒三角符号就是梯度。梯度是函数关于每一个自变量的偏导组成的向量。物理意义就是一个在站在某一个点上，斜率最大的那个方向。（最常见的就是二维平面上曲线的斜率）。

二、二阶逼近与牛顿法

对损失函数进行二阶展开：

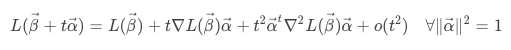
损失函数取得最小值的必要条件是：

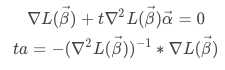
最后得到β的迭代公式：

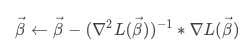
牛顿法需要用到Hessian矩阵，是损失函数的二阶导数组成的矩阵。于是上面的公式就变成了：

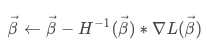
牛顿法要求Hessian矩阵必须是非负定的，才能求解出局部最小值。。

ps：当Hessian矩阵非正定时，收敛到局部最大值，不定时，收敛到鞍点。

另外，如果Hessian矩阵是病态的（求解方程组时如果对数据进行较小的扰动，则得出的结果具有很大波动，这样的矩阵称为病态矩阵。用条件数来衡量，矩阵A的条件数：K(A)=‖A^-1‖*‖A‖。若K很大的时候，A为病态矩阵），需要通过正则化来处理，求伪逆。则损失函数的参数更新方程：