优先队列式分支限界法-最小重量机器设计问题

Posted 2021-01-12 kk980414

问题描述：

设某一机器由n个部件组成，每一种部件都可以从m个不同的供应商处购得。设是从供应商j处购得的部件i的重量，是相应的价格。试设计一个优先队列式分支限界法，给出总价格不超过d的最小重量机器设计。

[之所以想记录这个问题，是因为我觉得自己"用各个部件的最小重量作为未来最理想重量"的这个设计还挺特别。其他都是实验报告中的内容]

算法描述:

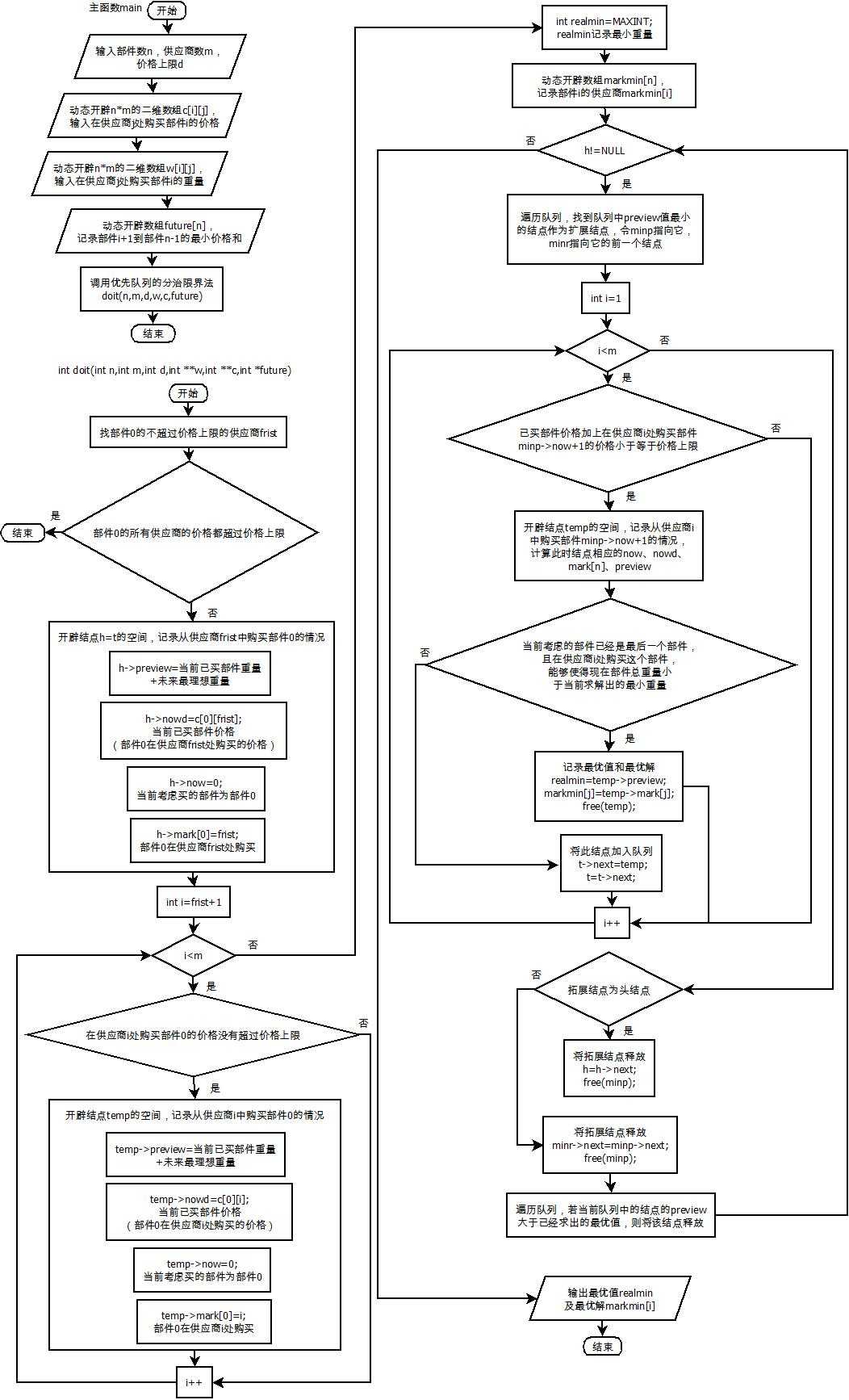
算法实现：

#include<stdio.h>
#include<stdlib.h>

struct NodeType
{
    int *mark;    //记录部件i的供应商
    int preview;    //当前已买部件重量+未来最理想重量
    int now;    //当前考虑买的部件
    int nowd;    //当前已买部件价格
    struct NodeType* next;
};

#define MAXINT 65534;
int doit(int n,int m,int d,int **w,int **c,int *future)
{
    int frist=0;
    while(frist<m&&c[0][frist]>d)
       frist++;
    //找第一个部件的不超过价格上限的供应商frist
    if(frist==m)return 0; 
    //第一个部件的所有供应商的价格都超过价格上限，无法购买

    /*
    构造优先队列的第一个结点
    */
    struct NodeType *h,*t,*temp;
    h=t=temp=temp=(struct NodeType *)malloc(sizeof(struct NodeType));
    temp->mark=(int *)malloc((sizeof(int))*n);
　　 temp->preview=future[0]+w[0][frist];    //当前已买部件重量+未来最理想重量
    temp->now=0;        //当前考虑买的部件为部件0
　　 temp->nowd=c[0][frist]; //当前已买部件价格（部件0在供应商frist处购买的价格）
    temp->mark[0]=frist;    //部件0在供应商frist处购买
    temp->next=NULL;
    for(int i=frist+1;i<m;i++)
    {
        if(c[0][i]<=d)    //若在供应商i处购买部件0的价格没有超过价格上限（约束剪枝）
        {
            temp=(struct NodeType *)malloc(sizeof(struct NodeType));
            temp->mark=(int *)malloc((sizeof(int))*n);
            temp->preview=future[0]+w[0][i];//当前已买部件重量+未来最理想重量
            temp->now=0;   //当前考虑买的部件为部件0
            temp->nowd=c[0][i]; //当前已买部件价格（部件0在供应商i处购买的价格）
            temp->mark[0]=i;    //部件0在供应商i处购买
            temp->next=NULL;
            t->next=temp;
            t=t->next;
        }
    }
    int realmin=MAXINT;    //记录最小重量
    int *markmin;
    markmin=(int *)malloc((sizeof(int))*n);
　　//记录部件i的供应商markmin[i]
    struct NodeType *minr,*minp,*r,*q;
    while(h!=NULL)
    {
    /*
    找到队列中重量最小的结点作为扩展结点(minp)
    */
        int min=realmin;//-
         r=q=h; 
        while(q!=NULL)
        {        
            if(q->preview<min)
            {
                min=q->preview;
                minr=r;
                minp=q;
            }
            r=q;
            q=q->next;
        }
        for(int i=0;i<m;i++)
        {
            if(minp->nowd+c[minp->now+1][i]<=d)
            //若已买部件价格加上在供应商i处购买
　　　　　　　//部件minp->now+1的价格小于等于价格上限
            {
                temp=(struct NodeType *)malloc(sizeof(struct NodeType));
                temp->mark=(int *)malloc((sizeof(int))*n);
            /*
            当前已买部件重量+未来最理想重量
            */
                temp->preview=0;
                for(int j=0;j<(minp->now+1);j++)
                    temp->preview+=w[j][minp->mark[j]];    
　　　　　　　　　　//先计入之前已买的部件的重量
                temp->preview+=w[minp->now+1][i];    
　　　　　　　　　　//在计入当期在供应商i处购买部件minp->now+1的重量
                temp->preview+=future[minp->now+1];    
　　　　　　　　　　//最后计入未来最理想的重量
                temp->now=minp->now+1;    
　　　　　　　　　　//当前考虑买的部件为部件minp->now+1
                
                temp->nowd=minp->nowd+c[minp->now+1][i];
    　　　　　　　//当前之前已买部件价格+在供应商i处购买部件
　　　　　　　　　 //minp->now+1的价格
            /*
            记录之前已买部件的供应商+当前部件的供应商i
            */
                for(int j=0;j<(minp->now+1);j++)
                    temp->mark[j]=minp->mark[j];
                temp->mark[minp->now+1]=i;
                temp->next=NULL;
                
                if(temp->now+1==n&&temp->preview<realmin)    
　　　　　　　　　 //若当前考虑的部件已经是最后一个部件，
　　　　　　　　　 //且在供应商i处购买这个部件，
                //能够使得现在部件总重量优于当前求解出的最优值
                {
                    
                /*记录最优值和最优解*/
                        realmin=temp->preview;
                        for(int j=0;j<n;j++)markmin[j]=temp->mark[j];
                        free(temp);            
                }
                else
                {
                //若当前考虑的部件并非最后一个部件，将此结点加入队列
                    t->next=temp;
                    t=t->next;
                }
            }    
        }
        if(minp==h)//拓展结点为头结点
        {
            h=h->next;
            free(minp);//将拓展结点释放
        }
        else    //拓展结点非头结点
        {
            minr->next=minp->next;
            free(minp);//将拓展结点释放
        }
    /*
    如果当前队列中的结点的最理想重量大于已经求出的最优解，则将该结点释放
    */
        while(h->preview>=realmin&&h!=t)
        {
            q=h;
            h=h->next;
            free(q);
        }
        if(h->preview>=realmin)
        {
            free(h);
            h=NULL;
        }
    }
    /*
    输出最优值及最优解
    */
    printf("%d
",realmin);
    for(int i=0;i<n;i++)printf("%d ",markmin[i]+1);
    return 0;
}
int main()
{
    int n,m,d;
    scanf("%d %d %d",&n,&m,&d);//部件数，供应商数，价格上限
    int ** c;
    c=(int **)malloc((sizeof(int *))*n);
    for(int i=0;i<m;i++)
       c[i]=(int *)malloc((sizeof(int))*m);
    for(int i=0;i<n;i++)
       for(int j=0;j<m;j++)
          scanf("%d",&c[i][j]);
    //在供应商j处购买部件i的价格c[i][j]         
    int ** w;
    w=(int **)malloc((sizeof(int *))*n);
    for(int i=0;i<m;i++)
       w[i]=(int *)malloc((sizeof(int))*m);
    for(int i=0;i<n;i++)
       for(int j=0;j<m;j++)
          scanf("%d",&w[i][j]);
    //在供应商j处购买部件i的重量w[i][j]
    int * future;
    future=(int *)malloc((sizeof(int))*n);    
    for(int i=0;i<n;i++)
    {
        int min=MAXINT;
        for(int j=0;j<m;j++ )
           if(min>w[i][j]) min=w[i][j];
        future[i]=min;
    }
    for(int i=0;i<n-1;i++)
    {
       future[i]=0;
       for(int j=i+1;j<n;j++)
         future[i]+=future[j];
    }
    future[n-1]=0;
    //购买完部件i后剩余部件的最理想重量
    doit(n,m,d,w,c,future);
    //优先队列分支限界算法
    return 0;
}