Luogu4609 FJOI2016 建筑师 第一类Stirling数

Posted 2021-01-12 itst

题目传送门

题意：给出$N$个高度从$1$到$N$的建筑，问有多少种从左往右摆放这些建筑的方法，使得从左往右看能看到$A$个建筑，从右往左看能看到$B$个建筑。$N leq 5 imes 10^4 , A,B leq 100$

---

第一次看到第一类$Stirling$数有用emmm

考虑将某种方案中最高的建筑拿出来，将分成的两半中可以看得见的与被它挡住的建筑分成一个部分，如下

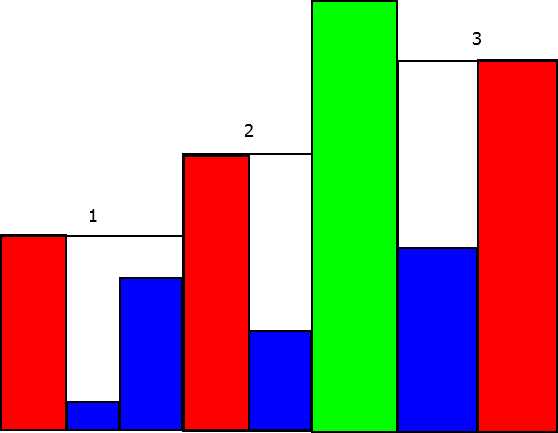
绿色的当然是最高的，剩下的两个部分分成了1,2,3三个部分。可以知道我们总共需要$A+B-2$这样的部分，而其中$A-1$个放在左边，$B-2$个放在右边，所以答案中会有一项$C_{A+B-2}^{A-1}$

考虑如何产生这$A+B-2$个部分。可以发现每一个部分的产生就是一个圆桌排列的产生（相当于在圆桌排列上选择高度最高的建筑，将其拉成一条线，而同一圆桌排列得到的建筑的部分是一样的），所以我们需要让$N-1$个建筑产生$A+B-2$个圆桌排列，也就是$S_{N-1}^{A+B-2}$

又因为圆桌排列扯成一个排列的方式只有一种，且划分左右之后，排列方式也只有一种，所以答案就是$$C_{A+B-2}^{A-1} imes S_{N-1}^{A+B-2}$$

预处理$50000 imes 200$的$Stirling$数和$200 imes 200$的组合数就好

注意：$S_0^0=C_{0}^{0} = 1$

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 using namespace std;
 4 
 5 const int MOD = 1e9 + 7;
 6 ll Stir[50001][201] , yh[201][201];
 7 
 8 int main(){
 9     yh[0][0] = Stir[0][0] = 1;
10     for(int i = 1 ; i <= 200 ; i++){
11         yh[i][0] = 1;
12         for(int j = 1 ; j <= i ; j++)
13             yh[i][j] = (yh[i - 1][j - 1] + yh[i - 1][j]) % MOD;
14     }
15     for(int i = 1 ; i <= 50000 ; i++)
16         for(int j = 1 ; j <= i && j <= 200 ; j++)
17             Stir[i][j] = (Stir[i - 1][j - 1] + Stir[i - 1][j] * (i - 1)) % MOD;
18     int K;
19     for(cin >> K ; K ; K--){
20         int a , b , c;
21         cin >> a >> b >> c;
22         cout << Stir[a - 1][b + c - 2] * yh[b + c - 2][b - 1] % MOD << endl;
23     }
24     return 0;
25 }