数学,位运算,典型题
Posted codemaker-li
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学,位运算,典型题相关的知识,希望对你有一定的参考价值。
数学,自然想到组合数,逆元,阶乘
先来一发组合数相关,
#define MAXN 200001 const int mod=1000000007; typedef long long ll; int n,m,r,c; ll ans,s; ll inv[MAXN],fac[MAXN],dev[MAXN]; //inv[]逆元,fac[]阶乘,dev[]阶乘的逆元 void chuli(int x) { inv[1]=1; fac[1]=1; dev[1]=1; fac[0]=1; dev[0]=1; for (int i=2;i<=x;i++) { fac[i]=fac[i-1]*i%mod; inv[i]=inv[mod%i]*(mod-mod/i)%mod; dev[i]=dev[i-1]*inv[i]%mod; } } ll C(int n,int m) { // C (m) // (n) ll x=fac[n]*dev[n-m]%mod*dev[m]%mod; return x; }
这是最普通的了,
然后是一些典型题,
No.1
∑i=1n ∑j=i n Ai and Ai+1~~Aj
这道题要逐个位数去统计贡献
#include <iostream> #include <cstdio> #define ll long long using namespace std; int W,n,line[100002]; ll ans; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&line[i]); while(line[i]>>W)W++; } for(int w=0;w<W;w++) for(int i=1,j=1;i<=n;i=++j) if((line[i]>>w)&1){ while(j<=n&&(line[j]>>w)&1)j++; ans+=((ll)j-(ll)i)*(j-i+1)/2*(1<<w); } printf("%lld",ans); return 0; }
然后还有对xor的优化
1 ll num_xor(ll x) { 2 int modans=x%4; 3 if (modans==0) { 4 return x; 5 } 6 if (modans==1) { 7 return 1; 8 } 9 if (modans==2) { 10 return x+1; 11 } 12 return 0; 13 } 14 15 ll l,r; 16 scanf("%lld%lld",&l,&r); 17 ans=num_xor(r)^num_xor(l-1); 18 printf("%lld ",ans);
这个只是 l xor l+1 xor l+2 ~~ xor r
连续xor的结果
还有错排公式
来吧
错排问题,是组合数学中的问题之一。考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)。研究一个排列错排个数的问题,叫做错排问题或称为更列问题。
D(n)=(n-1)[D(n-1)+D(n-2)]; D(1)=0; D(2)=1。
错排也有例题
比如这个
求有多少种长度为 n 的序列 A,满足以下条件:
1 ~ n 这 n 个数在序列中各出现了一次。
若第 i 个数 A[i] 的值为 i,则称 i 是稳定的。序列恰好有 m 个数是稳定的。
满足条件的序列可能很多,序列数对 109+7 取模。
#include <cstdio> #include <iostream> #include <string> #include <bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e6; const ll mod=1e9+7; ll n,m,ans; ll f[N+5]; ll mul[N+5]; int T; void chuli() { //错排预处理 f[0]=1; f[1]=0; for (int i=2;i<=N;i++) { f[i]=((i-1)*(f[i-1]+f[i-2])%mod)%mod; } //阶乘预处理 mul[0]=1; for (int i=1;i<=N;i++) { mul[i]=mul[i-1]*i%mod; } } //30~~43 求逆元 ll fast_pow(ll a,ll p) { ll ans=1; for (;p;p>>=1,a=a*a%mod) { if (p&1) { ans=ans*a%mod; } } return ans; } ll inv(ll x) { return fast_pow(x,mod-2); } ll get_C(ll n,ll m) { ll x=mul[n]%mod; ll y=mul[m]*mul[n-m]%mod; ll ans=x*inv(y)%mod; return ans; } int main () { chuli(); scanf("%d",&T); while (T--) { scanf("%lld%lld",&n,&m); ans=get_C(n,m)*f[n-m]%mod; printf("%lld ",ans); } return 0; }
位运算还有典型题
No.2
所以对于一个序列,求出它们所有的连续和来说,小明觉得十分的简单。但今天小明遇到了一个序列和的难题,这个题目不仅要求你快速的求出所有的连续和,还要快速的求出这些连续和的异或值。小明很快的就求出了所有的连续和,但是小明要考考你,在不告诉连续和的情况下,让你快速求是序列所有连续和的异或值。
解释:
一般这种异或都是按位一位一位做的
对于某第k位,如果为1,那么说明
所有连续和异或的这第k位为1
如果满足这第k位为1的(s[i]-s[j])有cnt个
如果cnt为奇数,那么说明答案的第k位也等于1
如何求出第k位为1的(i,j)对数?
如果sum[i]第k位为1:
为了使第k位为1,要么sum[j]第k位为0且sum[j]前k-1位小于sum[i]前k-1位的大小
原因是如果红色条件不成立,进位后就变成了0
还有就是sum[j]第k位为1且sum[j]前k-1位大于sum[i]前k-1位的大小
同理,也是进位的问题
那么红色部分要求满足大小关系的对数,用两个树状数组就行
第k位为0同理
还可以这么解释:
一般这种位运算的题都要把每一位拆开来看,因为位运算每个位的结果这和这一位的数有关。
这样我们用s[i]表示a的前缀和,即a[1]+a[2]+....a[i],然后我们从这些数二进制最右位(2^0)开始,按照每一位对答案的贡献来计算。
假设我们现在算到最右位(2^0),并且位于第i个数,我们想要知道以i结尾的连续和对答案的贡献,只需要知道有多少s[i]-s[j](0<=j<i)的2^0位是1。 (设s[0]=0)
如果这个数是奇数,就说明异或了1奇数次,也就相当于异或了1,我们只需要把记录这一位总的异或贡献的变量cnt异或1即可;
如果是偶数就不用管了,对答案没有贡献。
对于数的每一位如果最后cnt=1的话,就说明在这一位所有连续和的异或和为1,我们就需要把答案加上(1<<(这个位数))。
那如何快速计算有多少个s[i]-s[j]的二进制第k位是否为1呢??
答案是利用权值树状数组。
考虑到Σa 最大才有1000000,我们构造两棵权值树状数组,一棵记录当前位为1的,另一棵记录为0的。
如果当前扫描到的s[i]的二进制第k位为1,那么对这一位的答案有贡献的只有那些第k位为1且第k位向右的数比s[i]第k位向右的数大的或者第k位为0且第k位向右的数不比s[i]第k位向右的数大的。(可能有点拗口,,都怪我语文学的不好)
为什么呢?
因为如果第k位都为1的话,那么只有后面那些位的和大于s[i]的数,s[i]减去它之后第k位才能出现1(因为s[i]比它小的话需要向更高位借数,就和小学学的横式减法差不多),从而对答案作出贡献;
如果第k位为0的话,如果后面再比s[i]大的话,s[i]第k位的1就需要借给低一位的了,所以后面必须不比s[i]大。
就是这样
1 #include <cstdio> 2 #include <iostream> 3 #include <string> 4 #include <bits/stdc++.h> 5 6 using namespace std; 7 #define MAXN 1000001 8 int c[MAXN][2]; 9 int s[MAXN],a[MAXN],ans; 10 int pw[21],n; 11 12 void add(int x,int y) { 13 while (x<=1000000) { 14 c[x][y]++; 15 x+=(x&(-x)); 16 } 17 } 18 int query(int x,int y) { 19 int sum=0; 20 while (x) { 21 sum+=c[x][y]; 22 x-=(x&(-x)); 23 } 24 return sum; 25 } 26 int main() { 27 int flag,cnt; 28 cin>>n; 29 for (int i=1; i<=n; i++) { 30 scanf("%d",&s[i]); 31 s[i]+=s[i-1]; 32 } 33 pw[0]=1; 34 for (int i=1; i<=20; i++) 35 pw[i]=pw[i-1]*2; 36 for (int i=0; i<=20; i++) { 37 if (pw[i]<=s[n]) { 38 memset(c,0,sizeof(c)); 39 flag=0; 40 add(1,0); 41 for (int j=1; j<=n; j++) { 42 int tmp=s[j]&pw[i]; 43 if (tmp) { 44 cnt=query(a[j]+1,0)+query(1000001,1)-query(a[j]+1,1); 45 } 46 else { 47 cnt=query(a[j]+1,1)+query(1000001,0)-query(a[j]+1,0); 48 } 49 if (cnt%2==1) flag^=1; 50 add(a[j]+1,(bool)tmp); 51 if (tmp) { 52 a[j]|=pw[i]; 53 } 54 } 55 if (flag) { 56 ans|=(pw[i]); 57 } 58 } 59 } 60 cout<<ans; 61 return 0; 62 }
最后还要有小球与盒子的问题
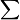




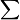




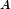




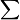




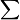




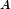




以上是关于数学,位运算,典型题的主要内容,如果未能解决你的问题,请参考以下文章

