快速排序

Posted 2021-01-12 fengzeng666

1、选主元

如果每次都选取第一个元素为主元，则时间复杂度为O(n^2)。

所以建议主元选取方法为：选头中尾元素的中位数。(三数中值分割法)

 

2、代码实现（三数中值分割法）

 

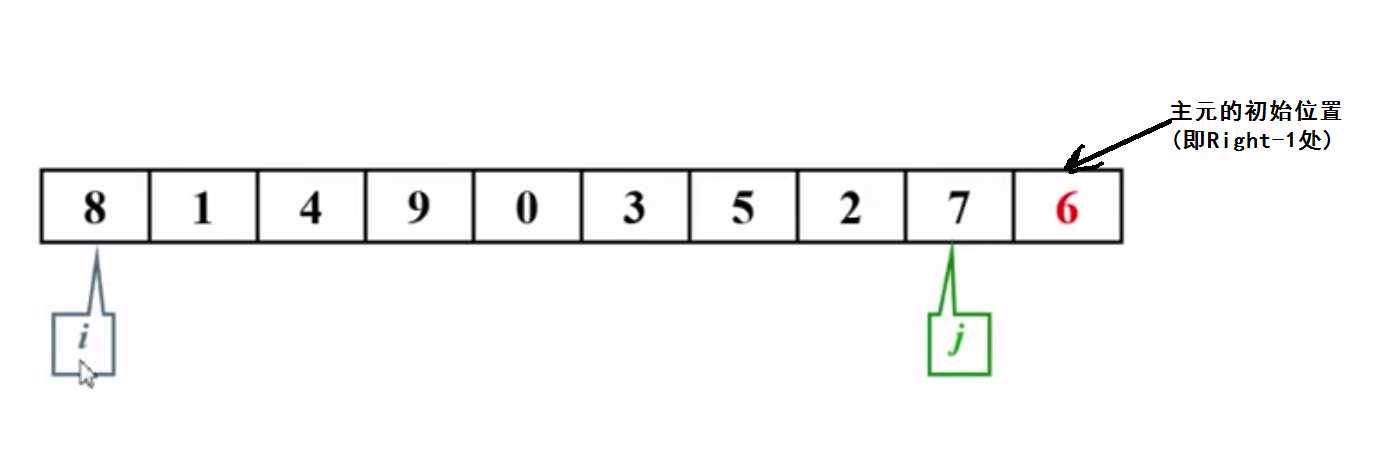
 1 #define Cutoff 100
 2 
 3 void Swap(ElementType *a, ElementType *b)
 4 {
 5     ElementType tmp = *a;
 6     *a = *b;
 7     *b = tmp;
 8 }
 9 
10 //选主元
11 ElementType Median3( ElementType A[], int Left, int Right )
12 {
13     int Center = (Left + Right) / 2;
14     
15     if(A[ Left ] > A[ Center ])
16         Swap( &A[ Left ], &A[ Center ] );
17     if(A[ Left ] > A[ Right ])
18         Swap( &A[ Left ], &A[ Right ] );
19     if(A[ Center ] > A[Right])
20         Swap(&A[ Center ], &A[ Right ]);
21         
22     /*此时A[Left] <= A[Center] <= A[Right] ,所以三者中位数(即主元)为A[Center]*/
23     Swap(&A[ Center ], &A[ Right-1 ]); // 将主元藏在最右边, 即A[Right]的左侧
24     
25     /*A[Left]此时肯定小于A[Center], A[Right]肯定大于A[Center], 
26       并且两者已经分居在主元的两侧,又把主元藏在了A[Right-1], 
27       所以只需考虑A[Left+1]与A[Right-2]之间的元素*/
28     return A[ Right-1 ];  //返回主元
29 }
30 
31 //快速排序的递归函数
32 void QSort( ElementType A[], int Left, int Right )
33 {
34     int Pivot, i, j;
35     if( Right-Left >= 3 )    //如果序列元素充分多，进入快排
36     {
37         Pivot = Median3( A, Left, Right );   //选主元
38  /*a*/  i = Left;
39         j = Right - 1;
40         while(1)     //将序列中比主元小的移动到主元左边，大的移动到右边
41         {
42  /*b*/      while( A[++i] < Pivot ) {}       
43             while( A[--j] > Pivot ) {}      
44             if( i < j ) 
45                 Swap( &A[i], &A[j] );
46             else
47                 break;
48   }
49         Swap( &A[i], &A[Right-1] );    //此时i左边的元素都比主元小，右边的都比主元大，所以i为主元的正确位置
50         QSort( A, Left, i-1  );        //递归解决左边
51         QSort( A, i+1, Right );        //递归解决右边
52     }
53     else
54         InsertionSort( A+Left, Right-Left+1 );   //元素个数小于等于2时，必须用简单排序处理
55 }
56 
57 
58 //快速排序的统一接口
59 void QuickSort( ElementType A[], int N )
60 {
61     QSort( A, 0, N-1 );
62 }

 

 注意：

( 1 ) 不能把a, b处的程序改为

i = Left + 1; 
j = Right - 2;
while( A[i] < Pivot )   ++i;
while( A[j] > Pivot )   --j;

否则将出错，因为当A[ i ] = A[ j ] = pivot 的时候，会产生一个无限循环 ( 死循环 ). 

 

( 2 ) 当A[ i ] 或 A[ j ]与pivot时，i和j必须停下来做交换，否则如果数组中全部元素都相等的话，i 将一直移动到倒数第二个位置，

这样将会使一趟过后主元只向左移动一个位置，使得运行时间变为O(n^2).

 

( 3 ) Cutoff的值至少要为3，否则对两个数或一个数无法进行三数中值的选择，且只有一个数的时候，Left与Right相等。数组会越界。

当间隔( Right - Left )小于2时，必须进行简单排序，不然快速排序会出现错误。

因为：

(1)当 Right - Left 等于 0时,快排的元素个数只有一个，当这个数位于数组的最后位置时，当++i后，再访问A[ i ], 就会出现数组越界的错误！

 

(2) 当 Right - Left 等于 1时，快排的元素个数只有2个，假设这两个数是4,5且为数组最后两个数，那么选出的主元就是4，当 --j 后，A[ j ]就会访问到4前面的那个数，

 但你只是对4,5进行快排，当j访问到前面的数时， 就导致快排出现错误的结果。且如果这两个数是数组前两个数的话，--j 就会导致数组越界。

 

(3)快速排序只能将小于主元的数放在主元左边，大于主元的数放在右边，某次快排后把5,4排在了主元3的右边，但并不能继续把5和4排好序。所以此时必须借助简单排序。比如，

　　　　　　若缺少下面这条简单排序的语句， 比如对A[8] = { 8, 1, 4, 9, 0, 3, 5, 2}，快速排序将会出现错误，输出为0,1,2,3,5,4,8,9。

 　　　　else
    　　　　   InsertionSort( A+Left, Right-Left+1 );

 

 

3、快速排序存在的问题