简单而不失优美的SVD分解

Posted 2021-01-12 sugar-mouse-wbz

一.  引子——高维空间与西瓜

这学期选课有一门“网络数据挖掘”，原来特别担心与本学期选的一门“模式识别与数据挖掘”在一定程度上相重复，不过还好，这个老师讲课不是照本宣科，讲得更多的是个人的理解还有从业经验。

今天讲得挺有意思的一点是，在讲到聚类的时候，老师有些嗤之以鼻，说在高维空间内，聚类算法可能并不会像我们想的那么理想，比如我们在使用k-means算法的时候，我们通常认为数据的分布（在二维）是这样的：

 

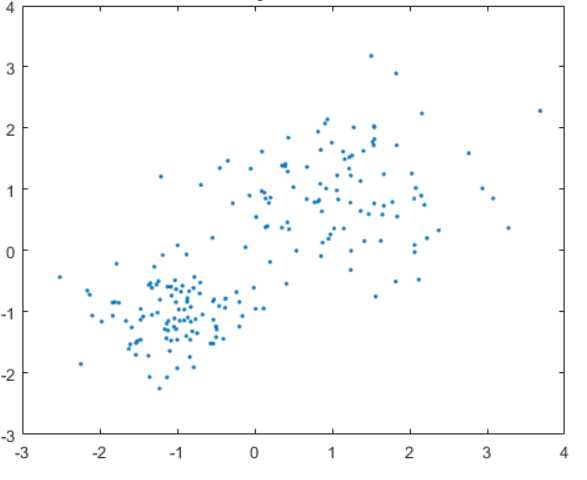
但是往往情况可能并不是如我们所看到的那样直观，就比如我们如果假设在数据分布在一维空间内，而且样本分布大概占总取值区间的一半：

那么我们直观地有：

$${R_{sample1d}} = {1 over 2}$$

进一步，如果我们是在二维空间，在每个维度上，样本取值区间也是总取值区间地一半，那么样本分布空间占总空间的大小：

$${R_{sample2d}} = {1 over 4}$$

于是可以继续这样递推，可想而知，如果认为在高维空间内样本取值域是一个超球体（像一个西瓜），那么有些出人意外地，在我们不太care的瓜皮部分，是占据了绝大部分空间的。

前面讲这些，算是一个引子，我们对于高维空间的认识，要比我们自己认为的迟钝得多，而恰恰很讽刺的是，我们所面临的问题往往都是高维数据，我们对此的做法往往也只有凭借数学工具去探索，此时任何主观的假设往往都会背离实际。

二. SVD分解介绍

1. 模型介绍

开始讲一下SVD分解。

其实SVD分解不是一个概率模型，甚至跟我们平时遇到的非概率模型不一样。

平时我们遇到的SVD分解，往往是求一个判别面，比如感知机、SVM等（决策树是多个分类面）

SVD分解的优美性在于，仅仅凭借纯数学的代换，就完成复杂的聚类分析，并且提供了数值依据，没有任何歧义。

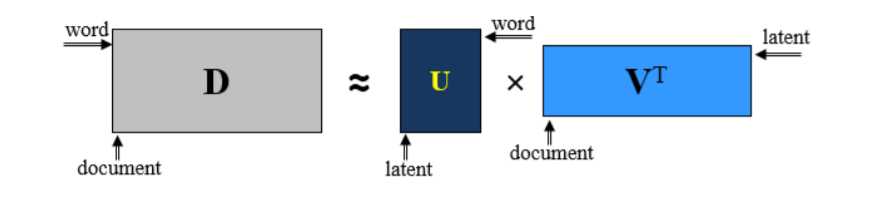
简单的讲，SVD分解，就是将原来的矩阵A拆分成三个矩阵的乘积，这三个矩阵分别是U、Σ、V

也即

$$A = USigma {V^T}$$

其中，V描述了原始空间中的正交基，U描述了相关空间的正交基，Σ描述了V中的向量变成U中的向量时被拉伸的倍数。

2. 模型应用

有关于SVD的分解的应用，有很多，简要的提点一下，但是不展开来讲。

（1）聚类划分（推荐系统、文本挖掘。。。）

　　这种应用场景是将原矩阵D看作是一种概率分布矩阵（但是并不一定归一化）

　　那么很明显，整个矩阵的分解过程恰好可以写成对于这个条件概率的一种分解，具体可以参考苏剑林的博客为什么SVD意味着聚类。

 

 （2）数据除噪

　　即按照能量大小将那些噪音项设置为0，从而滤除掉数据的噪音。

 （3）数据压缩

　　SVD分解本来就是将一个大矩阵拆解为几个小矩阵，这种压缩尤其在数据稀疏性和低秩性的时候表达的更加充分。

三. SVD分解的数学推导

　　SVD分解本来仅仅只是一种数学上的一种变换。

　　我们知道，一个矩阵（方阵）变换相当于一种线性空间变换。

　　具体来讲：

　　（1）一个正交基组成的矩阵对应这一个旋转拉伸变换

　　（2）一个对角矩阵对一个拉伸变换

　　（3）一个单位正交基对应的矩阵（正交矩阵）对应一个旋转变换

　　其推导可以从以下参考这两个博客

　　(1)特征值分解，奇异值分解(2)奇异值分解(SVD)原理详解及推导　

　　以上两篇博客都是从针对普通方阵的特征值分解过渡到针对矩阵的奇异值分解，而且引入了奇异值分解的几何意义。

四. SVD分解的意义

　　我们可能要提出问题，为什么SVD分解就意味着聚类呢

　　我们可以这样看：

　（1）SVD分解是将一个矩阵分解为它的左特征空间矩阵和右特征空间矩阵，而中间的特征值矩阵则是代表着权值，因此我们每次只要选取那些重要的特征留存下来，就可以几乎没有损耗的还原原矩阵。

　（2）我们可以看到，对于左特征矩阵的每一个聚类和每一个右特征矩阵的聚类是一一对应的，这也是合理的，因为在原矩阵中他们就是彼此依存的，同时，UV矩阵都是对于原矩阵的一种表达，它们具有一一映射关系。

　（3）SVD分解可以看成是原矩阵的一种低秩表达，也就是说由于原矩阵表示的项目之间必然是有一定耦合关系的，因此原矩阵不管是从行看还是从列看，都必然有很多线性相关（或近似）关系，这也是聚类的一个很重要前提。