数据结构之二叉树

Posted 2021-01-12 exman

基础概念　　

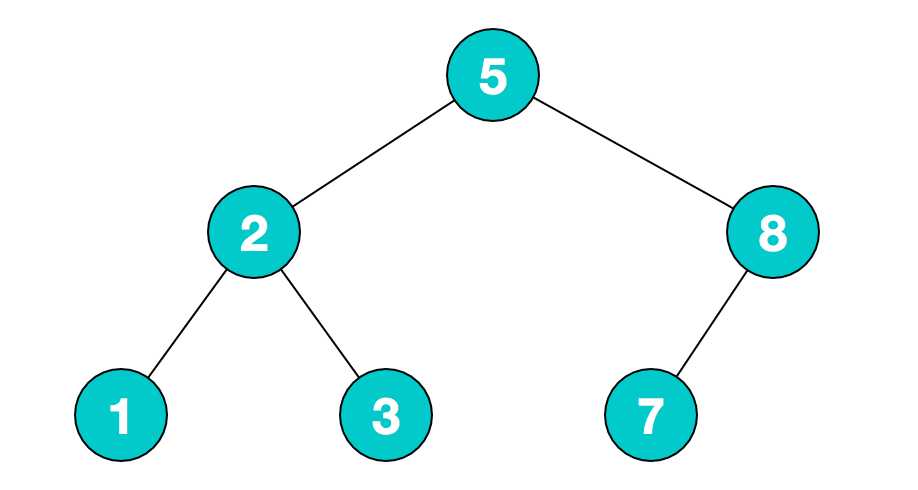
　　二叉树(binary tree)是一棵树，其中每个结点都不能有多于两个儿子。

　　二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

　　　　（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；

　　　　（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

　　　　（3）左、右子树也分别为二叉排序树；

 

二叉树的遍历

　　二叉树的遍历是指从根节点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。二叉树的遍历方式有很多，主要有前序遍历，中序遍历，后序遍历。

前序遍历

　　前序遍历的规则是：若二叉树为空，则空操作返回，否则先访问根节点，然后前序遍历左子树，再前序遍历右子树

 

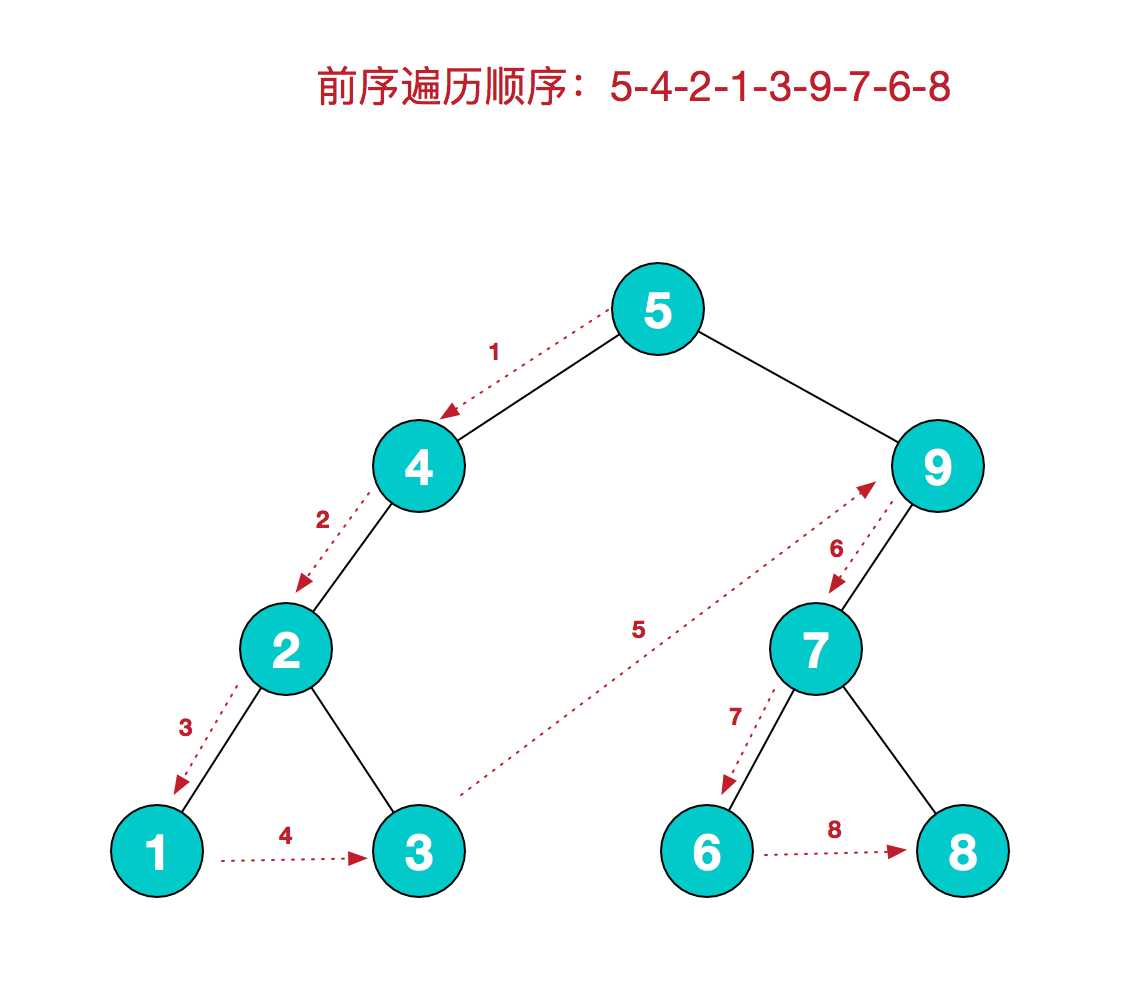
中序遍历

 　　中序遍历的规则是:若树为空，则空操作返回；否则从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后是访问根节点，最后中序遍历右子树。可以看到，如果是二叉排序树，中序遍历的结果就是个有序序列。

 

 

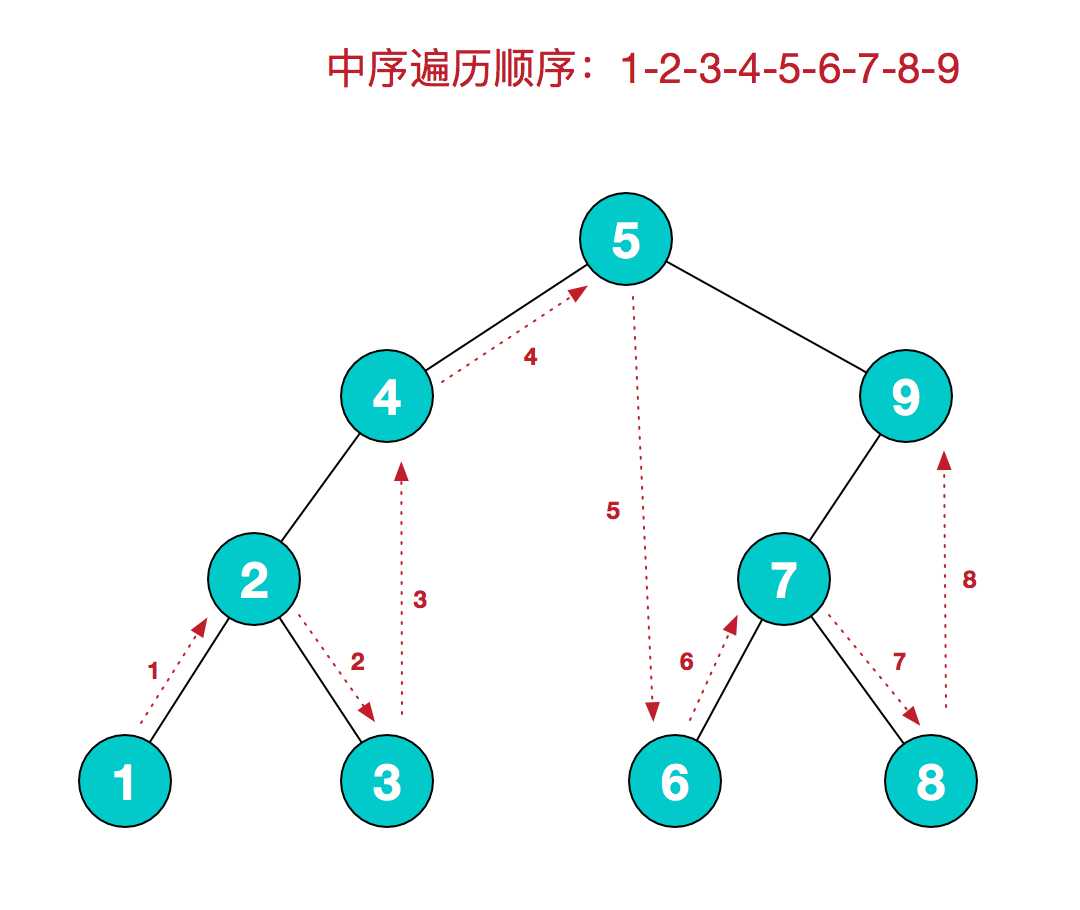
后序遍历

　　后序遍历的规则是:若树为空，则空操作返回；然后先遍历左子树，再遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。

 

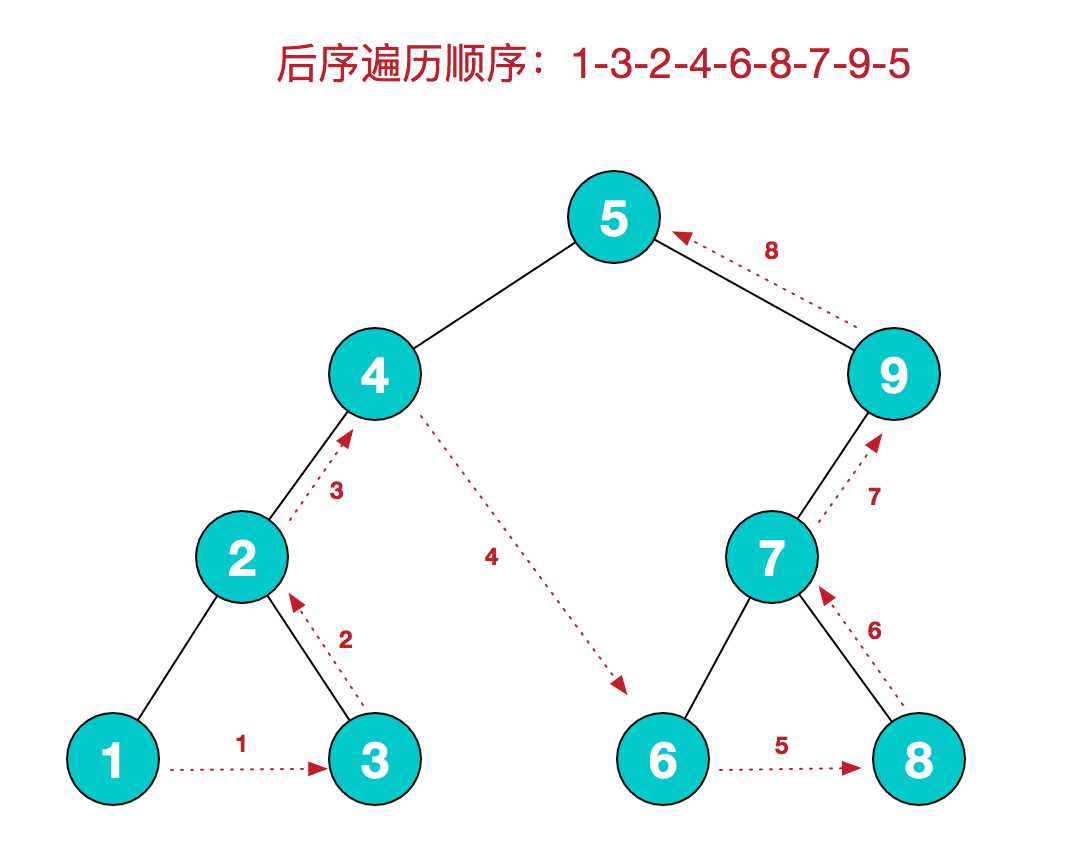
删除结点

　　对于二叉排序树的其他操作，比如插入，遍历等，比较容易理解；而删除操作相对复杂些。对于要删除的结点，有以下三种情况：

　　　　1.叶子结点；

　　　　2.仅有左子树或右子树的结点；

　　　　3.左右子树都有结点；

　　对于1（要删除结点为叶子结点）直接删除，即直接解除父节点的引用即可，对于第2种情况（要删除的结点仅有一个儿子），只需用子结点替换掉父节点即可；而对于要删除的结点有两个儿子的情况，比较常用处理逻辑为，在其子树中找寻一个结点来替换，而这个结点我们成为中序后继结点。

 

 

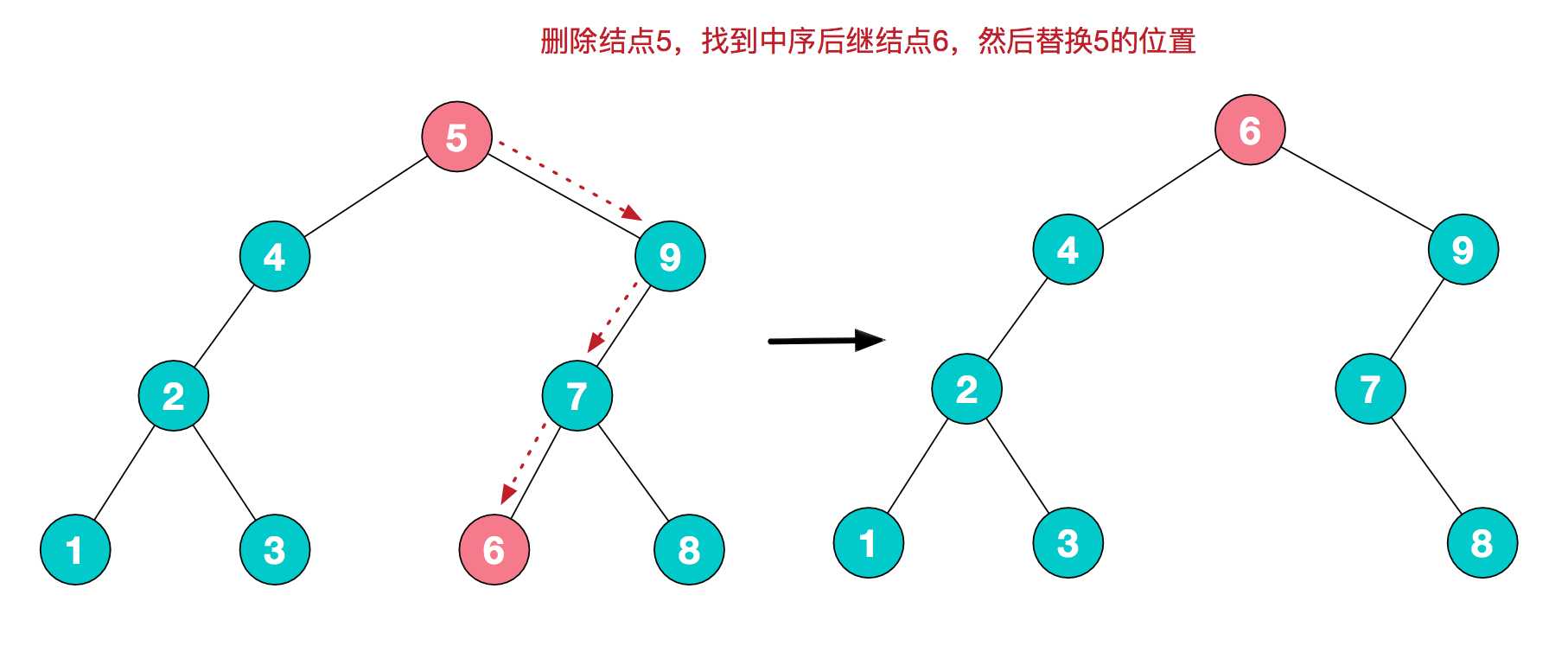
　　可以看到，我们找到的这个用来替换的结点，可以是删除结点的右子树的最小结点（6），也可以是其左子树的最大结点（4），这样可以保证替换后树的整体结构不用发生变化。为什么称为中序后继结点呢？我们来看下这棵树的中序遍历结果 1-2-3-4-5-6-7-8-9。可以很清晰的看到，其实要找的这个结点，可以是结点5的前驱或者后继。

代码实现

 二叉树的基本操作

执行结果

前序遍历：
5 2 1 3 8 6 10 
中序遍历：
1 2 3 5 6 8 10 
后序遍历：
1 3 2 6 10 8 5 
找到结点，其值为：10
删除结点8,中序遍历：5 2 1 3 10 6