常用激活函数比较

Posted 2021-01-11 vancuicide

本文结构：

1. 什么是激活函数
2. 为什么要用
3. 都有什么
4. sigmoid、ReLU、softmax的比较
5. 如何选择

---

1. 什么是激活函数

如下图，在神经元中，输入的inputs通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。

---

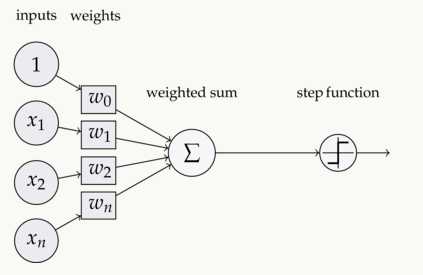
2. 为什么用

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

---

 

3. 都有什么

（1） sigmoid函数

公式： 

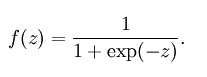
曲线：

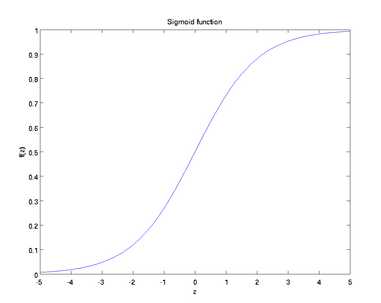
也叫Logistic函数，用于隐层神经元输出

取值范围为（0， 1）

它可以将一个实数映射到(0, 1)的区间，可以用来作为二分类。

在特征相差比较复杂或相差不是特别大时效果比较好。

下面解释为何会出现梯度消失：

反向传播算法中，要对激活函数求导，sigmoid的导数表达式为：

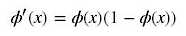
sigmoid原函数及导数图形如下：

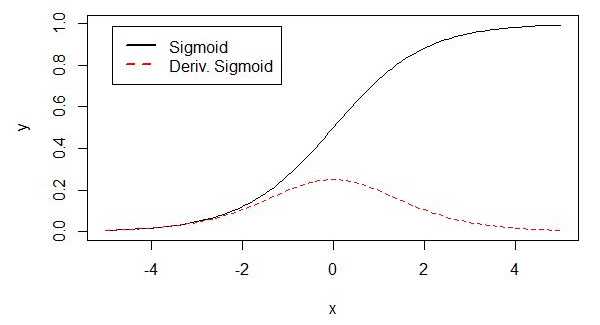
由图可知，导数从0开始很快又趋近于0了，易造成“梯度消失”现象

（2） Tanh函数

公式

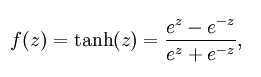
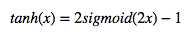
曲线

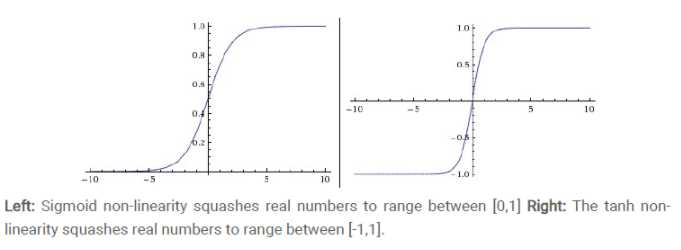
也称为双切正切函数

取值范围为[-1, 1]

tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。

与sigmoid的区别是，tanh是0均值的，因此实际应用中tanh会比sigmoid更好

（3） ReLU

Rectified Linear Unit(ReLU) - 用于隐层神经元输出

公式

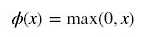
曲线

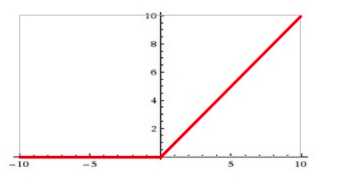
输入信号<0时，输出都是0，>0的情况下，输出等于输入

Krizhevsky et al. 发现使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多

ReLU的缺点：

训练的时候很“脆弱”，很容易就“die”了

例如，一个非常大的梯度流过一个ReLU神经元，更新过参数后，这个神经元再也不会对任何数据有激活现象了，那么这个神经元的梯度就永远都会是0

如果learning rate很大，那么很有可能网络中的40%的神经元都“dead”了

（4） softmax函数

 softmax - 用于多分类神经网络输出

公式

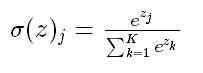
举个例子来看看公式的意思：

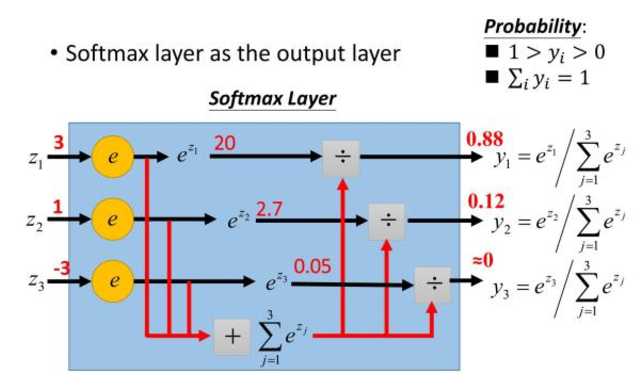
如果某一个zj大过其他z，那这个映射的分量就逼近于1，其他就逼近于0，主要应用就是多分类。

为什么要取指数，第一个原因就是要模拟max的行为，所以要让大的更大。

第二个原因是需要一个可导的函数。

---

4. sigmoid，ReLU，softmax的比较

sigmoid和ReLU的比较：

sigmoid的梯度消失问题，ReLU的导数就不存在这样的问题，它的函数表达式如下：

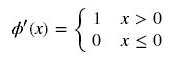
曲线如图所示

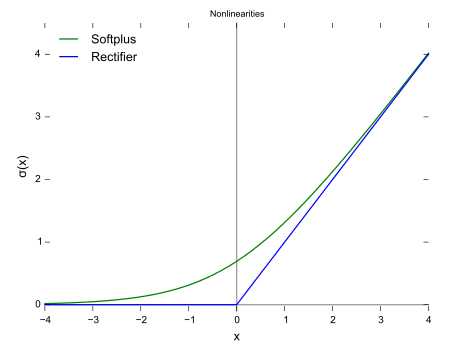
对比sigmoid类函数主要变化是：

1. 单侧抑制
2. 相对宽广的兴奋边界
3. 稀疏激活性

sigmoid和softmax的区别：

softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1.

sigmoid将一个real value映射到（0,1）的区间，用来做二分类。

而 softmax 把一个 k 维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中 bi 是一个 0～1 的常数，输出神经元之和为 1.0，所以相当于概率值，然后可以根据 bi 的概率大小来进行多分类的任务。

二分类问题时 sigmoid 和 softmax 是一样的，求的都是 cross entropy loss，而 softmax 可以用于多分类问题

softmax是sigmoid的扩展，因为，当类别数 k＝2 时，softmax 回归退化为 logistic 回归。具体地说，当 k＝2 时，softmax 回归的假设函数为：

利用softmax回归参数冗余的特点，从两个参数向量中都减去向量θ1 ，得到:

最后，用 θ′ 来表示 θ2?θ1，上述公式可以表示为 softmax 回归器预测其中一个类别的概率为

另一个类别概率的为

这与 logistic回归是一致的。

softmax建模使用的分布是多项式分布，而logistic则基于伯努利分布
　　
多个logistic回归通过叠加也同样可以实现多分类的效果，但是 softmax回归进行的多分类，类与类之间是互斥的，即一个输入只能被归为一类；多个logistic回归进行多分类，输出的类别并不是互斥的，即”苹果”这个词语既属于”水果”类也属于”3C”类别。

---

5. 如何选择

选择的时候，就是根据各个函数的优缺点来配置，例如：

如果使用 ReLU，要小心设置 learning rate，注意不要让网络出现很多 “dead” 神经元，如果不好解决，可以试试 Leaky ReLU、PReLU 或者 Maxout.