10.10校内测试线段树维护第k小+删除lca+主席树维护前驱后驱

Posted 2021-01-11 wans-caesar-02111007

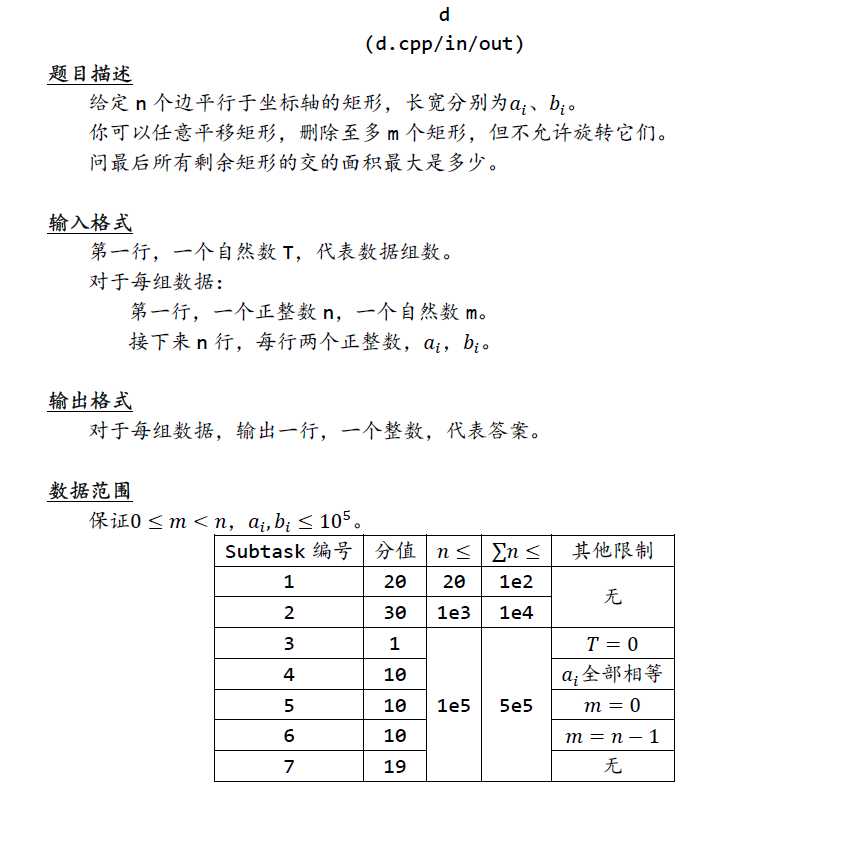
贪心思想。将a排序后，对于每一个a，找到对应的删除m个后最小的b，每次更新答案即可。

如何删除才是合法并且最优的？首先，对于排了序的a，第$i$个那么之前就应该删除前$i-1$个a对应的b。剩下$m-i+1$可以删，那么在剩下的b中查找第$m-i+2$小即可。每次做完就删除当前a对应的b。

注意离散化。

还有数组不要开大了....

#include<bits/stdc++.h>
#define LL long long
using namespace std;

void read(int &x) {
    x = 0; int t = 1; char ch = getchar();
    while(ch > ‘9‘ || ch < ‘0‘)    { if(ch == ‘-‘)    t = -1; ch = getchar(); }
    while(ch >= ‘0‘ && ch <= ‘9‘) {
        x = x * 10 + ch - ‘0‘;
        ch = getchar();
    }
    x = x * t;
}

int a[500005], b[500005], n, m;

struct Node {
    int a, b;
    int ida, idb;
} mat[100005];
bool cmp(Node a, Node b) { if(a.a == b.a)    return a.b < b.b; return a.a < b.a; }

int siz[400005], val[400005];

void modify(int nd, int l, int r, int pos, int d) {
    if(l == r) {
        siz[nd] += d;
        return ;
    }
    int mid = (l + r) >> 1;
    if(pos <= mid)    modify(nd << 1, l, mid, pos, d);
    else            modify(nd << 1 | 1, mid + 1, r, pos, d);
    siz[nd] = siz[nd << 1] + siz[nd << 1 | 1];
}

int query(int nd, int l, int r, int pos) {
    if(l == r)    return val[l];
    int mid = (l + r) >> 1;
    if(pos <= siz[nd << 1])    return query(nd << 1, l, mid, pos);
    else return query(nd << 1 | 1, mid + 1, r, pos - siz[nd << 1]);
}

int pos[100005];
void work() {
    sort(b + 1, b + 1 + n);
    int q = unique(b + 1, b + 1 + n) - b - 1;
    
    memset(siz, 0, sizeof(siz));
    sort(mat + 1, mat + 1 + n, cmp);
    for(int i = 1; i <= n; i ++) {
        pos[i] = lower_bound(b + 1, b + 1 + q, mat[i].b) - b;
        val[pos[i]] = mat[i].b;
        modify(1, 1, q, pos[i], 1);
    }
    
    LL ans = 0;
    int r = min(mat[1].b, query(1, 1, q, m + 1));
    ans = 1ll * mat[1].a * r;
    for(int i = 1; i <= m; i ++) {
        modify(1, 1, q, pos[i], -1);
        int res = m - i + 1;
        r = query(1, 1, q, res);
        if(mat[i + 1].b < r)    r = mat[i + 1].b; 
        LL now = 1ll * mat[i + 1].a * r;
        ans = max(ans, now);
    }
    
    printf("%lld
", ans);
}

int main() {
    freopen("d.in", "r", stdin);
    freopen("d.out", "w", stdout);
    int T;
    scanf("%d", &T);
    while(T --) {
        read(n); read(m);
        for(int i = 1; i <= n; i ++) {
            read(mat[i].a); read(mat[i].b);
            b[i] = mat[i].b;
        }
        work(); 
    }
    return 0;
}

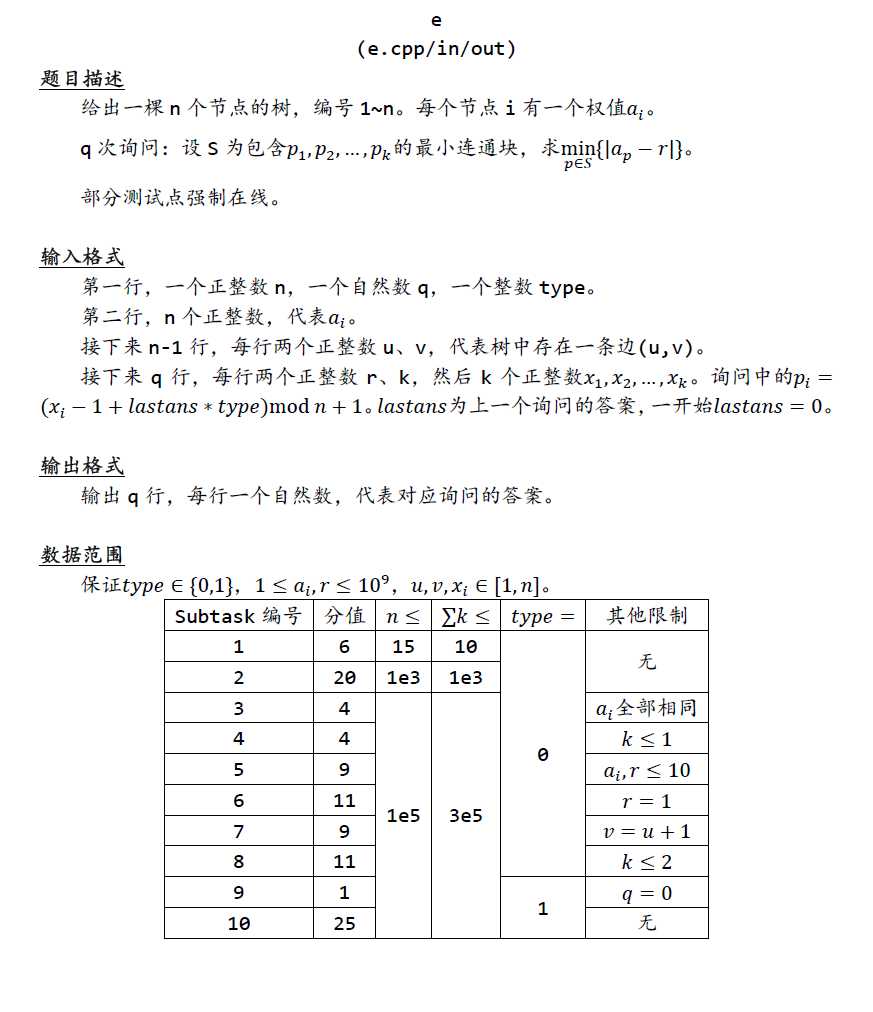
依旧是数据结构。我们发现，对于一个点集，它们一定有一个lca，而满足包含所有点的最小点集就是所有点到这个lca的链上的所有点。再加上题目要求最小的$abs(a[u]-r)$，就是用每条链上r的前驱和后驱来更新答案。

用主席树维护即可。每个结点的版本是由它的父亲结点转移过来。这样做查询的时候直接取出当前结点和lca的父亲结点的版本即可。

关于这个前驱和后驱的计算可以学习一下。

#include<bits/stdc++.h>
#define LL long long
using namespace std;

const int maxn = 1e9;

void read(int &x) {
    x = 0; int t = 1; char ch = getchar();
    while(ch > ‘9‘ || ch < ‘0‘)    { if(ch == ‘-‘)    t = -1; ch = getchar(); }
    while(ch >= ‘0‘ && ch <= ‘9‘) {
        x = x * 10 + ch - ‘0‘;
        ch = getchar();
    }
    x = x * t;
}

int n, q, type;

struct Node {
    int v, nex;
    Node(int v = 0, int nex = 0) :
        v(v), nex(nex) { }
} Edge[200005];

int h[100005], stot;
void add(int u, int v) {
    Edge[++stot] = Node(v, h[u]);
    h[u] = stot;
}

int sum[32*100005], ls[32*100005], rs[32*100005], tail;
inline int newnode(int x) {
    sum[++tail] = sum[x];
    ls[tail] = ls[x]; rs[tail] = rs[x];
    return tail;
}

inline void update(int nd) {
    sum[nd] = sum[ls[nd]] + sum[rs[nd]];
}

int insert(int nd, int l, int r, LL pos) {
    nd = newnode(nd);
    sum[nd] ++;
    if(l == r)    return nd;
    int mid = (l + r) >> 1;
    if(pos <= mid)    ls[nd] = insert(ls[nd], l, mid, pos);
    else rs[nd] = insert(rs[nd], mid + 1, r, pos);
    update(nd);
    return nd;
}

int queryl(int nd1, int nd2, int l, int r, int pos) {
    if(sum[nd1] == sum[nd2])    return 0;///这个结点下面没有新的点
    if(l == r)    return l;
    int mid = (l + r) >> 1;
    if(pos <= mid)    return queryl(ls[nd1], ls[nd2], l, mid, pos);
    else {
        int tmp = queryl(rs[nd1], rs[nd2], mid + 1, r, pos);////尽量往靠近pos的地方走
        if(tmp)    return tmp;///如果走不到就尽量往mid走
        else return queryl(ls[nd1], ls[nd2], l, mid, mid);
    }
}

int queryr(int nd1, int nd2, int l, int r, int pos) {
    if(sum[nd1] == sum[nd2])    return 0;
    if(l == r)    return l;
    int mid = (l + r) >> 1;
    if(pos > mid)    return queryr(rs[nd1], rs[nd2], mid + 1, r, pos);
    else {
        int tmp = queryr(ls[nd1], ls[nd2], l, mid, pos);
        if(tmp)    return tmp;
        else return queryr(rs[nd1], rs[nd2], mid + 1, r, mid);
    }
}

int dep[100005], jum[100005][21];
int lca(int u, int v) {
    if(dep[u] < dep[v])    swap(u, v);
    int t = dep[u] - dep[v];
    for(int p = 0; t; t >>= 1, p ++)
        if(t & 1)    u = jum[u][p];
    if(u == v)    return u;
    for(int p = 19; p >= 0; p --)
        if(jum[u][p] != jum[v][p])    u = jum[u][p], v = jum[v][p];
    return jum[u][0];
}

int rt[100005], a[100005];
void dfs(int u, int f) {
    jum[u][0] = f;
    for(int i = 1; i < 20; i ++)
        jum[u][i] = jum[jum[u][i - 1]][i - 1];
    dep[u] = dep[f] + 1;
    rt[u] = insert(rt[f], 1, maxn, a[u]);
    for(int i = h[u]; i; i = Edge[i].nex) {
        int v = Edge[i].v;
        if(v == f)    continue;
        dfs(v, u);
    }
}

int x[100005], p[100005];
int main() {
    freopen("e.in", "r", stdin);
    freopen("e.out", "w", stdout);
    scanf("%d%d%d", &n, &q, &type);
    for(int i = 1; i <= n; i ++)    read(a[i]);
    for(int i = 1; i < n; i ++) {
        int u, v;
        read(u); read(v);
        add(u, v); add(v, u);
    }
    dfs(1, 0);
    int lastans = 0;
    for(int i = 1; i <= q; i ++) {
        int r, k;
        scanf("%d%d", &r, &k);
        for(int j = 1; j <= k; j ++) {
            read(x[j]);
            p[j] = (x[j] - 1 + lastans * type) % n + 1;
        }
        int l = p[1];
        for(int j = 2; j <= k; j ++)
            l = lca(l, p[j]);
        l = jum[l][0];
        int res = maxn, tmp;
        for(int j = 1; j <= k; j ++) {
            tmp = queryl(rt[l], rt[p[j]], 1, maxn, r);
            if(tmp && r - tmp < res)    res = r - tmp;
            tmp = queryr(rt[l], rt[p[j]], 1, maxn, r);
            if(tmp && tmp - r < res)    res = tmp - r;
        }
        printf("%d
", res);
        lastans = res;
    }
    return 0;
}