最长公共子序列(LCS)

Posted 2021-01-11 xiugeng

一、最长公共子序列介绍

　　一个序列的子序列是在该序列中删去若干元素后得到的序列。例如：“ABCD”和“BDF”都是“ABCDEFG”的子序列。

　　最长公共子序列（Longest Common Subsequence,简写LCS）问题：给定两个序列X和Y，求X和Y长度最大的公共子序列。例如：X=“ABBCBDE”, Y="DBBCDB", LCS(X,Y)="BBCD"

　　应用场景：字符串相似度比对、基因比对。

1、LCS的最优子结构原理

　　令X=<x₁,x₂,...,x_m>和Y=<y₁,y₂,...,y_n>为两个序列，Z=<z₁,z₂,...,z_k>为X和Y的任意LCS。

　　1.如果x_m=y_n，则z_k=x_m=y_n且Z_k-1是X_m-1和Y_n-1的一个LCS。

　　2.如果x_m≠y_n，那么z_k≠x_m意味着Z是X_m-1和Y的一个LCS。

　　3.如果x_m≠y_n，那么z_k≠y_n意味着Z是X和Y_n-1的一个LCS。

2、最优解的递推式

　　

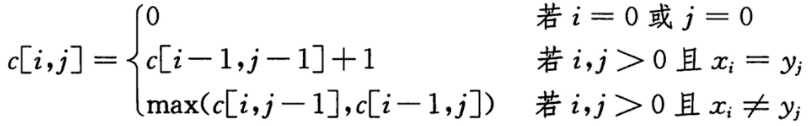
　　c[i,j]表示X_i和Y_j的LCS长度。

 二、示例及解析

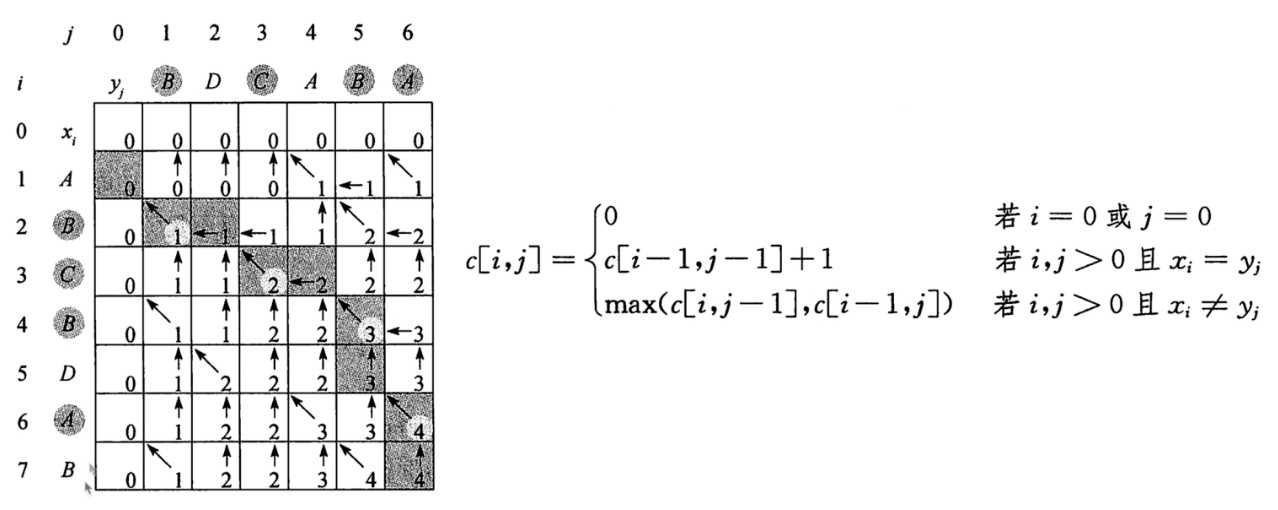
　　例如:要求a="ABCBDAB"与b="BDCABA"的LCS:

　　由于最后一位"B"=?"A"，因此LCS(a,b)应该来源于LCS(a[:-1],b)与LCS(a,b[:-1])中的一个。意思就是最后一位不一样，要不去除a的最后一位，要不去除b的最后一位。