chatGPT都可以干什么呢？来一睹风采 (送账号)

Posted 2023-03-04 听 风、

文章目录

• • • 1. 写代码
    • 2. 写文案
    • 3. 写剧本
    • 4. 写歌诗
    • 5. 写报告
    • 6. 查公式
    • 7. 写对联
    • 8. 写文章
    • 9. 做表格
    • 10. 做计划
    • 11. 等等

1. 写代码

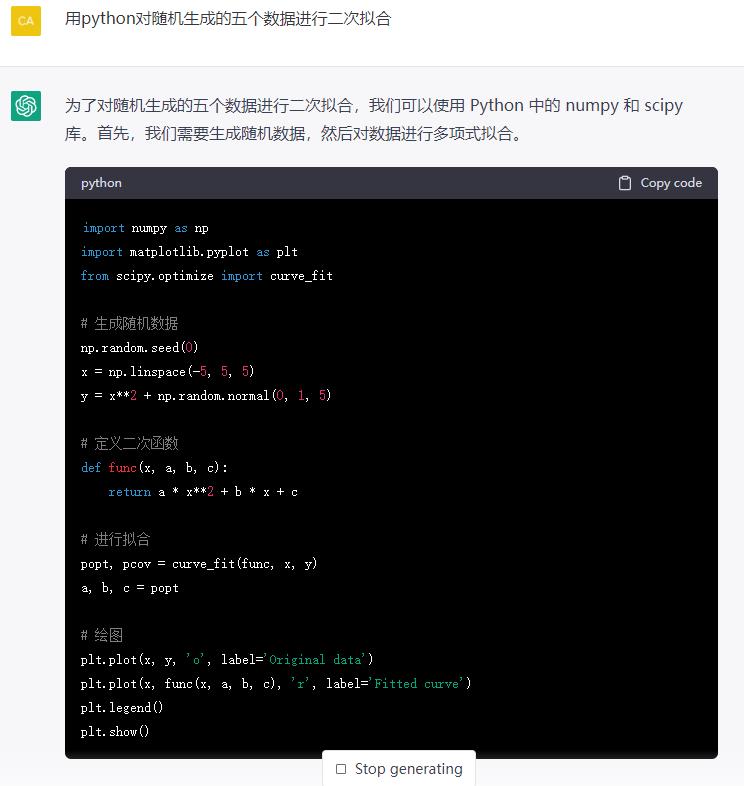
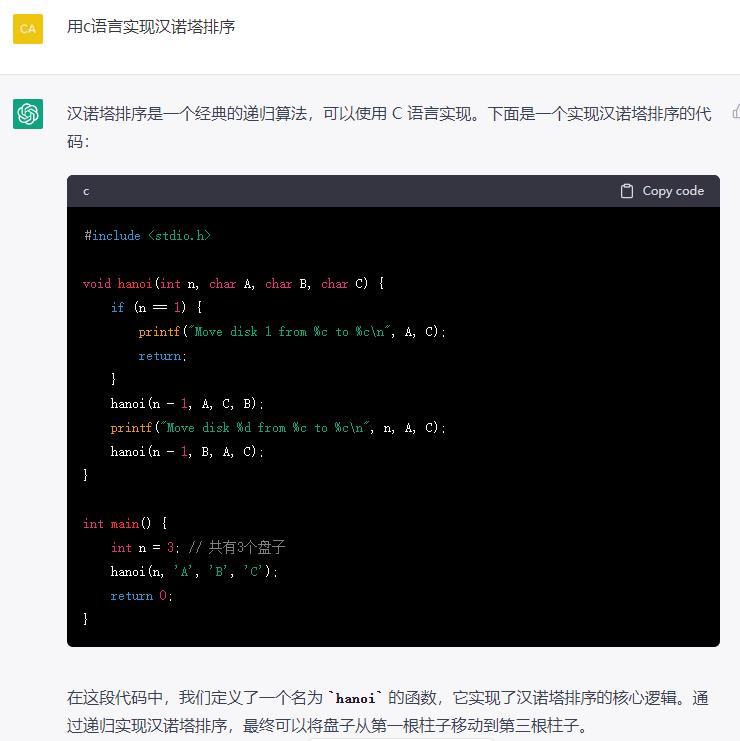
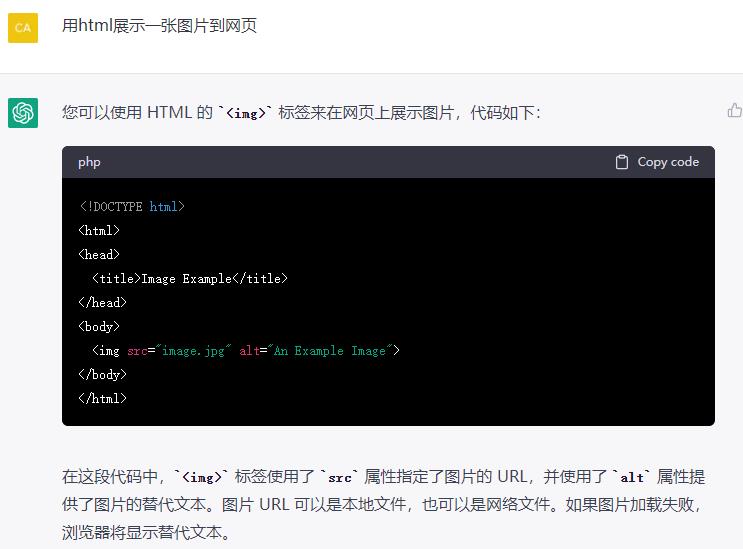
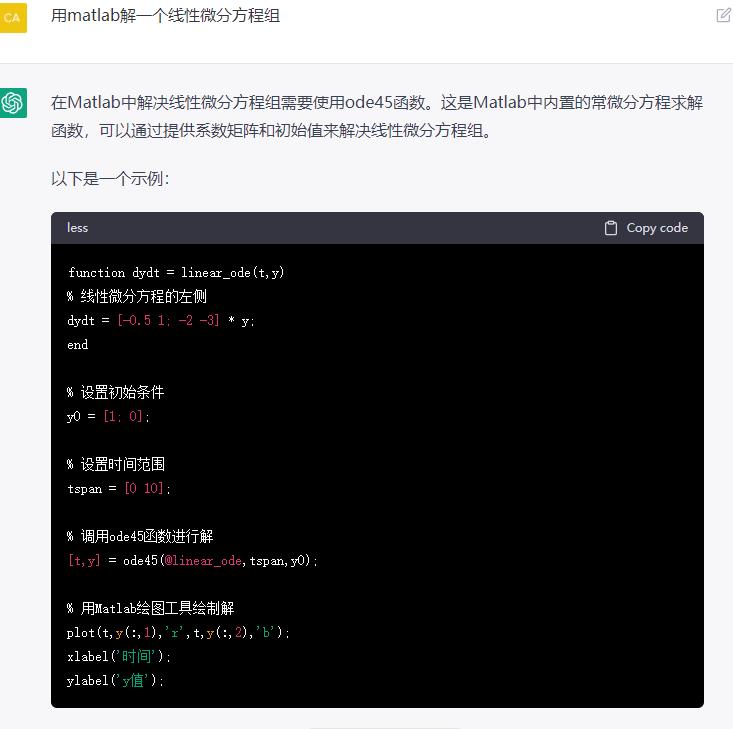
2. 写文案

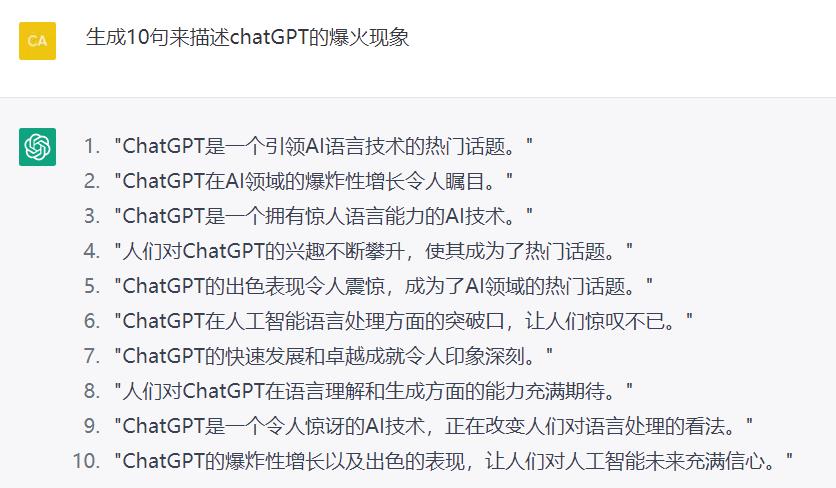
3. 写剧本

4. 写歌诗

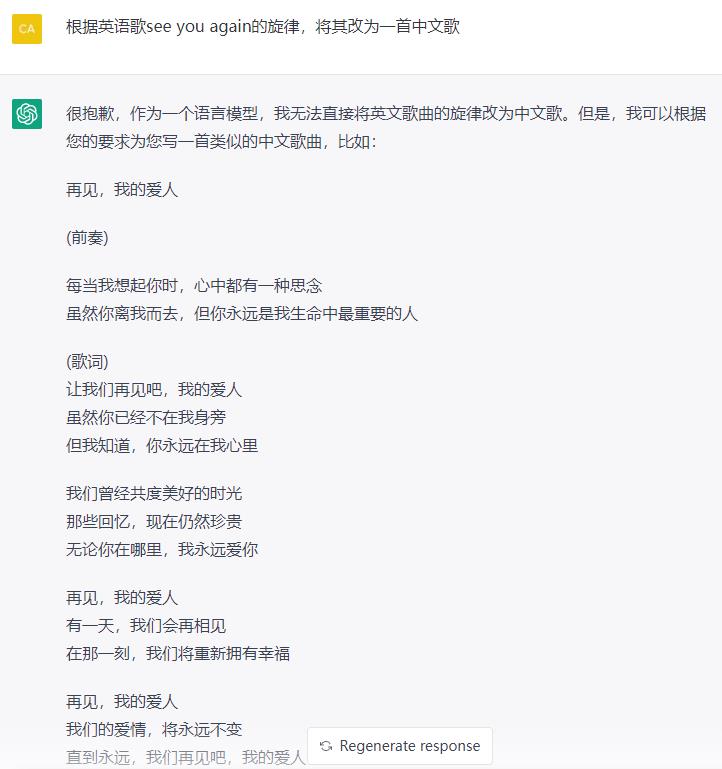
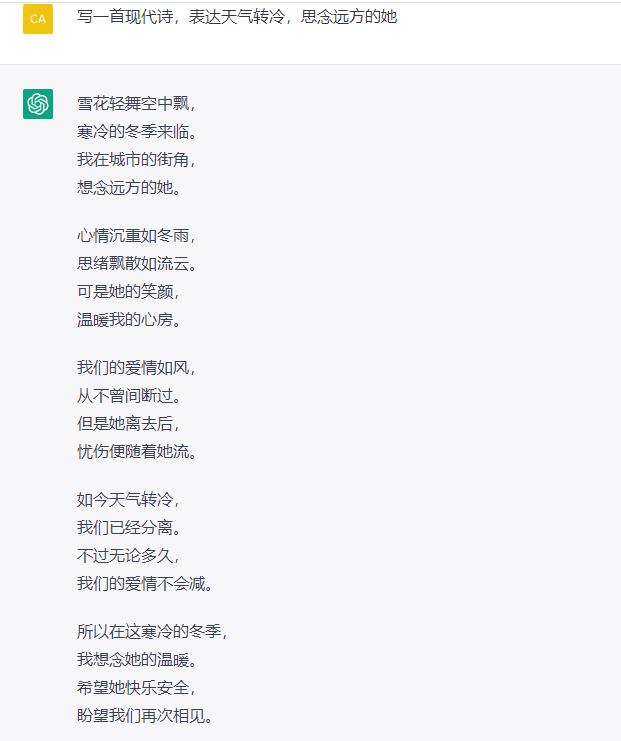
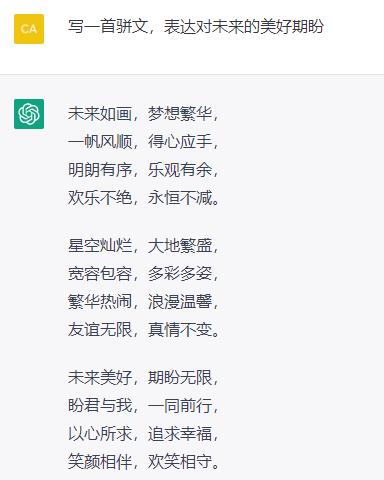
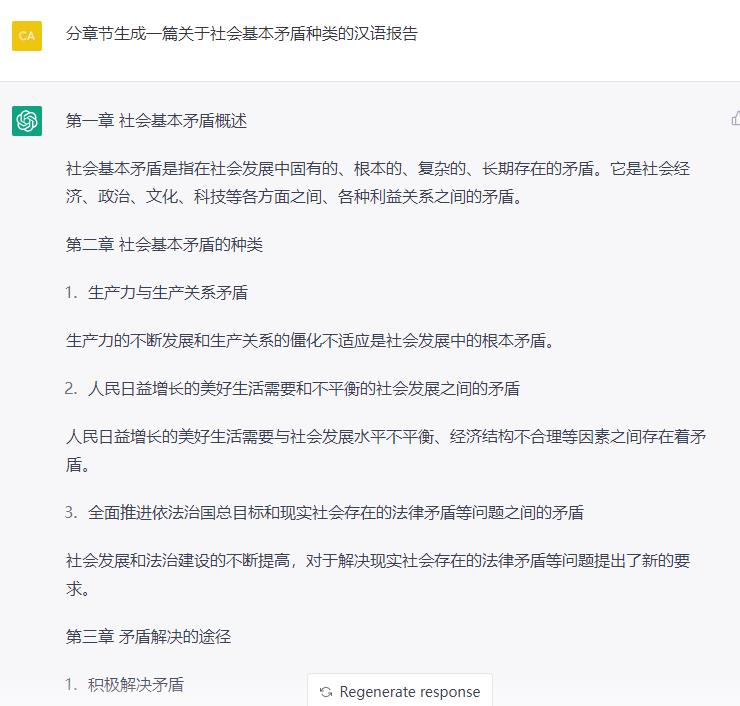
5. 写报告

这妥妥的翻译文，数据完全不对。

6. 查公式

傅里叶变换的时域性质有如下几点：

对称性：$\mathcal{F}(f(t))=\mathcal{F}(f(-t){)}^{\ast }$

循环卷积：$\mathcal{F}(f(t)\ast g(t))=\mathcal{F}(f(t))\cdot \mathcal{F}(g(t))$

时间平移：$\mathcal{F}(f(t-t_0))=e^{-j2\pi f_0{t}_0}\mathcal{F}(f(t))$

时间拓展：$\mathcal{F}(\alpha f(t))=\frac{1}{|\alpha |}\mathcal{F}(f(\frac{t}{\alpha }))$

时间反转：$\mathcal{F}(f(-t))=\mathcal{F}(f(t){)}^{\ast }$

以上是傅里叶变换的时域性质，其中，$\mathcal{F}$ 表示傅里叶变换，$f(t)$ 和 $g(t)$ 是时域信号，$\ast$ 表示循环卷积，${}^{\ast }$ 表示复共轭，$f_0$ 是信号的频率，$t_0$ 是时间平移量，$\alpha$ 是时间拓展量。

设原始的两个高斯分布分别为 $f(x)$ 和 $g(x)$，每个分布的平均值分别为 ${\mu }_1$ 和 ${\mu }_2$，标准差分别为 ${\sigma }_1$ 和 ${\sigma }_2$。
那么两个高斯分布相加后的结果为：
$$f(x)+g(x)=\frac{1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}}+\frac{1}{\sqrt{2\pi }{\sigma }_2}{e}^{-\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2}}$$通过简单的数学计算，得到这个结果的平均值 $\mu$ 和标准差 $\sigma$ 为：
$$\mu =\frac{{\mu }_1{\sigma }_2^2+{\mu }_2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}$$$$\sigma =\sqrt{\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}}$$

用 $f(t)$ 表示门函数，用 $g(t)$ 表示辛格函数，卷积的结果为：$$(f\ast g)(t)={\int }_{-\infty }^{\infty }f(\tau )g(t-\tau )d\tau$$由于 $f(t)$ 是一个门函数，其具有