131. Palindrome Partitioning

Posted 2021-01-11 skillking

一、题目

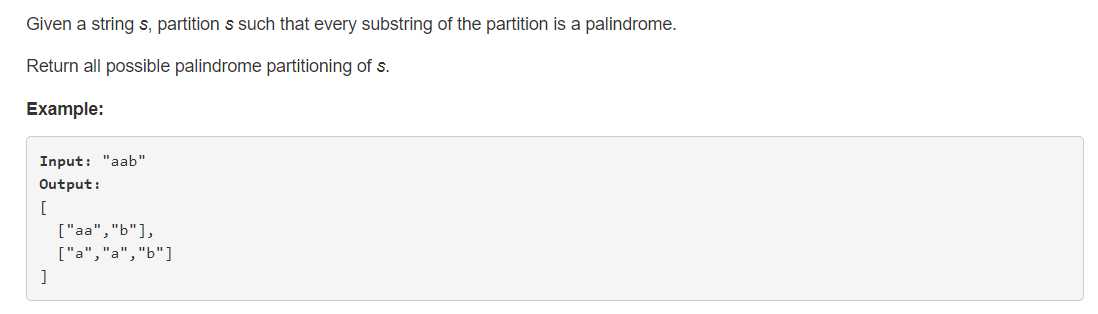
　　1、审题

　　

　　2、分析

　　　　给出一个字符串，将其分割成各个子串，使得其子串全为回文，求所有的分割方式。

 

二、解答

　　1、思路：　

　　　　方法一、

　　　　　　采用递归方式进行分割。

　　　　　　①、递归时，判断当前分割的子串是否为回文，若是，存储该子串，并分割字符串，继续递归剩下的子串；

　　　　　　②、递归跳出条件为： 当前字符串切割的字符下标 i >=  字符串的长度 ；

    public List<List<String>> partition(String s) {
        
        List<List<String>> resultList = new ArrayList<>();
        backTrack(resultList, new ArrayList<String>(), s, 0);
        return resultList;
    }
    private void backTrack(List<List<String>> resultList, ArrayList<String> curList, String s, int i) {
        
        if(curList.size() > 0 && i >= s.length()) {
            resultList.add(new ArrayList<String>(curList));
            return;
        }
        for (int j = i; j < s.length(); j++) {
            if(isPalindrome(s, i, j)) {
                curList.add(s.substring(i, j + 1));
                backTrack(resultList, curList, s, j + 1);
                curList.remove(curList.size() - 1);
            }
        }
    }
    private boolean isPalindrome(String s, int l, int r) {
        while(l < r) {
            if(s.charAt(l++) != s.charAt(r--))
                return false;
        }
        return true;
    }

 

　　　方法二、

　　　　采用 DP + DFS 进行实现。

　　　　采用一个动态数组 DP 记录是否为回文，代替每一次递归进行回文判断。 DP[i][j] = true: 表示 s 中 从下标 i 到 下标 j 之间的字符串是回文。

　　　　再采用递归进行 DFS 遍历，将 s 的所有切割的回文子串进行记录。

    public List<List<String>> partition2(String s) {
        
        List<List<String>> resultList = new ArrayList<>();
        boolean[][] dp = new boolean[s.length()][s.length()];
        
        for (int i = 0; i < s.length(); i++) {
            for (int j = 0; j <= i; j++) {
                if(s.charAt(j) == s.charAt(i) && (i - j <= 2 || dp[j+1][i-1])) {
                    dp[j][i] = true;
                }
            }
        }
        partitionHelper(resultList, new ArrayList<String>(), dp, s, 0);
        return resultList;
    }
    
    private void partitionHelper(List<List<String>> resultList, ArrayList<String> arrayList, 
                                boolean[][] dp, String s, int i) {
        if(arrayList.size() > 0 && i >= s.length()) {
            resultList.add(new ArrayList<>(arrayList));
            return;
        }
        for(int j = i; j < s.length(); j++) {
            if(dp[i][j]) {
                arrayList.add(s.substring(i, j + 1));
                partitionHelper(resultList, arrayList, dp, s, j + 1);
                arrayList.remove(arrayList.size() - 1);
            }
        }
    }