红黑树

Posted 2021-01-11 xmsx

目录

• 定义与性质
• 旋转
• 插入
• 删除

定义与性质

红黑树，是一种平衡的《二叉查找树》。

红黑树图示如下：

性质：

1. 结点要么是红的，要么是黑的。
2. 根结点是黑的。
3. 空结点是黑的。
4. 红色结点的两个儿子都是黑的。
5. 任一结点到空结点的每一条路径都包含相同数目的黑结点。

PS：空结点只是作为辅助使用，并不包含数据。

旋转

插入和删除时，为了继续保持红黑树的性质，对树进行旋转并重新着色。

下面是树的左旋与右旋图示：

插入

• 如果插入的是根结点，直接把此结点涂为黑色。
• 如果插入的结点的父结点是黑色，将此结点涂成红色。
• 如果插入的结点的父节点是红色，分为下面两种情况：

【红父红叔】

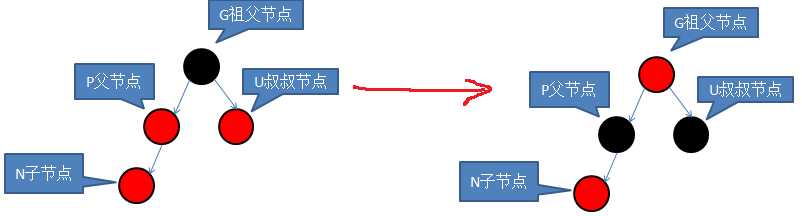
重新着色：黑父黑叔红祖父，如果祖父结点的父结点还是红色，那么就又是一个双红问题。

【红父黑叔】

乍一看，天然的红父黑叔是不存在的。

但是上述红父红叔问题可能转化为双红情况，这时就可能出现黑叔。

两种情况：

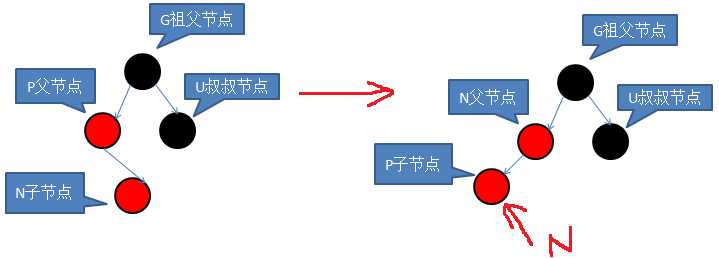
删除

【情况一：删除结点为叶结点】

• 若该结点是红色，则可直接删除，不影响红黑树的性质，算法结束。
• 若该结点是黑色，则删除后红黑树不平衡。（稍后讨论）

【情况二：删除结点只有一个子结点】

该结点为黑色（不可能为红色），其子结点为红色，子结点替代该结点位置颜色变黑。

【情况三：删除结点有两个子结点】

参考《二叉查找树》，相当于最左结点与被删结点交换了值，然后再删除最左结点，最左结点是叶结点，因此又回到了情况一。

下面重点探讨情况一中，叶结点为黑色的情况。

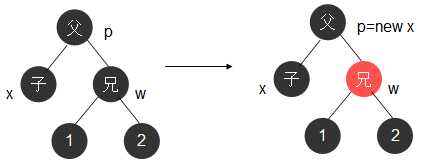
case1：红兄（黑父两黑侄是必然的）

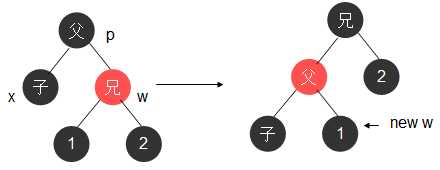
1. 做一次左旋并重新着色（如图）
2. 父染黑，1染红，删除结点（如case4）。

case2：黑兄左红侄右黑侄

1. 做一次右旋之后（如图）。
2. case3：黑兄右红侄。

case3：黑兄右红侄

1. 做一次左旋
2. 删除结点，红黑性质恢复。

case4：黑兄两黑侄红父

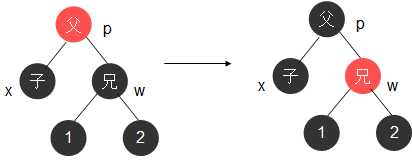
父染黑，兄染红，删除结点。

case5：黑兄两黑侄黑父

要想删除结点之后平衡，将兄染红。

但是此时，通过父结点的路径上的黑色结点比不通过...少了1个，因此需要从 case1 开始，对父结点重新平衡处理。