回溯法求解迷宫问题

Posted 2021-01-10 henuliulei

题目

这是我在老师发的PPT上发现的一道题，如下

 

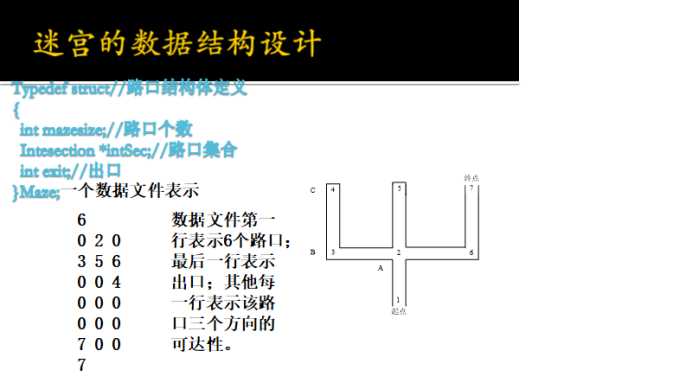
 1表示起点 7表示终点，一共六个路口,每个路口可以通达最多左上右三个路口，不能走的方向用0表示，求从1到7的路径。

求解思路：每个路口最多有三个搜索分支。把算法设计为如下的搜索过程：把整个搜索分解为向左、向前和向右三个方向上子问题的搜索。

当搜索到某个路口，发现该路口没有可搜索的方向时，就让搜索过程回溯到该路口的前一个路口，然后搜索这个路口的其他尚未搜索过的搜索方向。

样的搜索过程一直继续到找到出口或搜索完全部可连通路口的所有可能搜索方向没有找到出口为止。 

代码：

#include <bits/stdc++.h>
using namespace std;
int ro[100];//记录走过的路径
int k=-1;//路口数目
int flag=1;
int road(int a[][3],int m){
k++;//没经过一乐路口k就加1
for(int i=0;i<3;i++){
if(flag==0){//遇到终点结束
break;
}
if(a[m][i]==7){//找到终点输出走过的路径
cout <<"存在出口在"<<m +1<<"行"<<i+1<<"列" << endl;
cout<<"路径为" << "1" <<" ";
for(int s=0;s<k;s++){
cout <<ro[s]+1 << " " ;
}
flag=0;//表示探索结束
}
if(a[m][i]!=0){//探索路径
ro[k]=a[m][i]-1;
road(a,ro[k]);//递归下一个路口
}
else{
continue;//遇到0即没有路了跳过
}
}
k--;//该条路径不行，回溯到前一个路口
return 1;
}
int main()
{
int a[6][3];
for(int i=0;i<6;i++){
for(int j=0;j<3;j++){
cin >> a[i][j];
}
}
road(a,0);
return 0;
}

总结：该代码以PPT上的迷宫而写的，只需改一下参数便可以轻易扩展到一般的情况。