CF221C Circling Round Treasures

Posted 2021-01-10 oyjason

题目大意

给定一个$n imes m$的网格$(n,mleq 20)$，每个格子都是$Sspace #space Bspace xspace .$中第一个。

$S$表示起点，保证有且仅有一个。

$#$表示障碍，不能通过,$.$表示空地，可以通过

$B$表示炸弹，$x$是一个数字，每个数子代表着一个宝藏，每个宝藏有对应的价值（可以为负）。

炸弹和宝藏的数量不超过$8$个

现在你要规划一条从$S$出发，每次只能沿着上下左右四个方向，只能经过除了空地和起点的可以自交的闭合回路，使得这条回路缩圈起来的格子中不含有炸弹，将圈起来的格子中所有宝藏之和加起来记为$sum$，路径长度记为$len$，求$max(sum-len)$。

举个例子

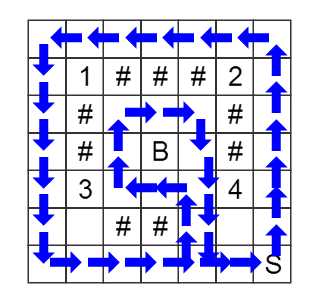
这遍是原图中的最优解。

 

题解

我们先想办法解决如何判断一个点是否在回路内。

考虑一个点$(i,j)$（第$i$行第$j$列），从它出发向左下作一条方向无限贴近于正下的射线，通过这条射线与回路相交次数的奇偶性来判断，即枚举所有$k(k>i)$，计算$sum$表示回路经过$(k,j),(k,j-1)$两个点之间的次数和。

若$sum$为奇数，那么在形内，否则在形外。

 

接下来就简单了，由于炸弹和宝藏的和不超过$8$个，我们直接将炸弹看做价值为$-INF$的宝藏，然后每个宝藏是否在形内进行装状态压缩。

这样就可以从起点出发进行$BFS$了，$F_{(i,j,k)}$表示从$S$出发，到达$(i,j)$，所有宝藏是否在形内的情况为$k$的最短步数。最后只需枚举状态进行计算取$max$即可。

最终复杂度为$O(nmk2^k)$，我图着省事把其中一个$k$改成了$n$也能过。

 

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define M 30
#define  bas 1000
#define INF 10000000
using namespace std;
int read(){
	int nm=0,fh=1; char cw=getchar();
	for(;!isdigit(cw);cw=getchar()) if(cw==‘-‘) fh=-fh;
	for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-‘0‘);
	return nm*fh;
}
const int dx[]={0,0,-1,1},dy[]={-1,1,0,0};
int n,m,q[INF],dis[M][M][550],pos[M][M],T,B,tot,val[M];
int xt[M],yt[M],xb[M],yb[M],hd,tl,Sx,Sy,ans;
char ch[M];
void ins(int x,int y,int sta){q[tl++]=(x*bas+y)*bas+sta;}
void tk(int &x,int &y,int &sta){sta=q[hd]%bas,q[hd]/=bas,y=q[hd]%bas,q[hd]/=bas,x=q[hd],hd++;}
int main(){
	n=read(),m=read(),memset(dis,0x3f,sizeof(dis));
	for(int i=1;i<=n;i++){
		scanf("%s",ch+1);
		for(int j=1;j<=m;j++){
			if(ch[j]==‘.‘) continue;
			if(ch[j]==‘B‘) B++,xb[B]=i,yb[B]=j,pos[i][j]=++tot,val[tot]=-INF;
			else if(ch[j]==‘#‘) pos[i][j]=-1;
			else if(ch[j]==‘S‘) ins(i,j,0),Sx=i,Sy=j,dis[i][j][0]=0;
			else ++T,xt[ch[j]-‘0‘]=i,yt[ch[j]-‘0‘]=j,pos[i][j]=++tot;
		}
	}
	for(int i=1;i<=T;i++) val[pos[xt[i]][yt[i]]]=read();
	while(hd<tl){
		int x,y,now; tk(x,y,now);
		for(int j=0;j<4;j++){
			int xx=x+dx[j],yy=y+dy[j],rem=now;
			if(pos[xx][yy]||xx<1||yy<1||xx>n||yy>m) continue;
			if(y!=yy){
				for(int j=1,nw=max(y,yy);j<xx;j++)
					if(pos[j][nw]>0) rem^=(1<<(pos[j][nw]-1));
			}
			if(dis[xx][yy][rem]<INF) continue;
			dis[xx][yy][rem]=dis[x][y][now]+1,ins(xx,yy,rem);
		}
	}
	for(int i=1;i<(1<<tot);i++){
		int res=0;
		for(int dt=1;dt<=tot;dt++) if((i>>(dt-1))&1) res+=val[dt];
		ans=max(ans,res-dis[Sx][Sy][i]);
	} printf("%d
",ans); return 0;
}