10.02 T3 打表找递推式+十进制快速幂 九校联考凉心模拟DAY1T1

Posted 2021-01-10 saionjisekai

题目背景

金企鹅同学非常擅长用1*2的多米诺骨牌覆盖棋盘的题。有一天，正 在背四六级单词的他忽然想：既然两个格子的积木叫“多米诺(domino)”，那 么三个格子的的积木一定叫“三米诺(tromino)”了！用三米诺覆盖棋盘的题 怎么做呢？

题目描述

用三米诺覆盖3n 的矩形棋盘，共多少种方案？三米诺可旋转；两种 方案不同当且仅当这两种图案直接覆盖在一起无法重叠。

输入输出格式

输入格式：

一行一个整数n(n<=10^40000)，表示棋盘列数。

输出格式：

一行一个整数，表示方案数，对998244353 取模。

输入输出样例

输入样例#1

2

输出样例#1

3

输入样例#2

3

输出样例#2

10

输入样例#3

29

输出样例#3

543450786

说明

对于10% 的数据，n <=5；
对于30% 的数据，n <=10^6；
对于40% 的数据，n <=20001000；
对于60% 的数据，n <=10^9；
对于80% 的数据，n <=10^1000
对于100% 的数据，n<=10^40000。

 

 

这题先爆搜把前面几项打表出来，然后上OEIS高斯消元把各项系数求出来，设a（n）为填满前n列的方案最后其实你可以得到一个东西

 

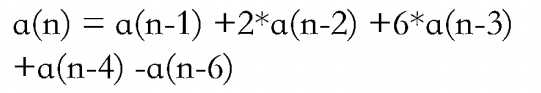
很显然直接上矩阵快速幂就可以了

但是数字这么大没法快速幂，发现一般的快速幂是2进制，我们就写十进制快速幂套一个二进制快速幂就可以了，其实我写了很久好难啊woc怎么会有这种东西就是按位快速幂就可以了（逃

取模多加点数字。。。负数把我坑惨了，顺便因为前六项只能打表，所以矩阵要乘n-6次，但字符串不好操作于是乘上6次矩阵的逆就可以了

code：

  1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdio>
  4 using namespace std;
  5 const long long mod=998244353;
  6 struct matrix{
  7     long long a[7][7];
  8 };
  9 long long chang[7][7]={
 10     {0,0,0,0,0,0,0},
 11     {0,1,1,0,0,0,0},
 12     {0,2,0,1,0,0,0},
 13     {0,6,0,0,1,0,0},
 14     {0,1,0,0,0,1,0},
 15     {0,0,0,0,0,0,1},
 16     {0,-1,0,0,0,0,0},
 17 };
 18 long long fan[7][7]={
 19     {0,0,0,0,0,0,0},
 20     {0,0,0,0,0,0,-1},
 21     {0,1,0,0,0,0,1},
 22     {0,0,1,0,0,0,2},
 23     {0,0,0,1,0,0,6},
 24     {0,0,0,0,1,0,1},
 25     {0,0,0,0,0,1,0},
 26 };
 27 matrix mul(matrix a,matrix b){
 28     matrix c;
 29     memset(c.a,0,sizeof c.a);
 30     for(long long i=1;i<=6;i++){
 31         for(long long j=1;j<=6;j++){
 32             for(long long k=1;k<=6;k++){
 33                 c.a[i][j]+=(a.a[i][k]%mod*b.a[k][j])%mod;
 34                 c.a[i][j]%=mod;    
 35             }
 36         }
 37     }
 38     return c;
 39 }
 40 matrix ksm(matrix a,long long b){
 41     matrix ans;
 42     memset(ans.a,0,sizeof ans.a);
 43     ans.a[1][1]=ans.a[2][2]=ans.a[3][3]=ans.a[4][4]=ans.a[5][5]=ans.a[6][6]=1;
 44     for(;b;b>>=1){
 45     //    cout<<b<<‘
‘;
 46         if(b&1)ans=mul(ans,a);
 47         a=mul(a,a);
 48     }
 49     return ans;
 50 }
 51 void tiaoshi(matrix ans){
 52         for(long long i=1;i<=6;i++){
 53         for(long long j=1;j<=6;j++)
 54         cout<<ans.a[i][j]<<" ";
 55         cout<<‘
‘;
 56     }    
 57 }
 58 int main(){
 59     freopen("tromino.in","r",stdin);
 60     freopen("tromino.out","w",stdout);
 61     string n;
 62     cin>>n;
 63     if(n.size()==1&&n[0]<=‘6‘){
 64         if(n=="1")cout<<1;
 65         if(n=="2")cout<<3;
 66         if(n=="3")cout<<10;
 67         if(n=="4")cout<<23;
 68         if(n=="5")cout<<62;
 69         if(n=="6")cout<<170;
 70         return 0;
 71     }
 72     matrix base,ans;
 73     memset(ans.a,0,sizeof ans.a);
 74     memset(base.a,0,sizeof base.a);
 75     for(long long i=1;i<=6;i++)
 76         for(long long j=1;j<=6;j++)
 77             base.a[i][j]=chang[i][j];
 78     ans.a[1][1]=ans.a[2][2]=ans.a[3][3]=ans.a[4][4]=ans.a[5][5]=ans.a[6][6]=1;
 79 //    for(long long i=1;i<=6;i++){
 80 //        for(long long j=1;j<=6;j++)
 81 //        cout<<base.a[i][j]<<" ";
 82 //        cout<<‘
‘;
 83 //    }    
 84     for(long long i=n.size()-1;i>=0;i--){
 85         long long num=n[i]-‘0‘;
 86     //    tiaoshi(ans);
 87     //    cout<<‘
‘;
 88     //    cout<<num<<endl;
 89         ans=mul(ans,ksm(base,num));
 90     //    tiaoshi(ans);
 91         base=ksm(base,10);
 92     }
 93     matrix ni;
 94     for(long long i=1;i<=6;i++)
 95         for(long long j=1;j<=6;j++)
 96             ni.a[i][j]=fan[i][j];
 97     for(long long i=1;i<=6;i++){
 98         ans=mul(ans,ni);
 99     }
100     cout<<(mod*3+ans.a[1][1]*170%mod+ans.a[2][1]*62%mod+ans.a[3][1]*23%mod+ans.a[4][1]*10%mod+ans.a[5][1]*3%mod+ans.a[6][1]*1%mod)%mod;
101     return 0;
102 }

优秀的复杂度（误

over