2016-2017 ACM-ICPC, NEERC, Northern Subregional Contest Problem I. Integral Polygons

Posted 2021-01-10 destr

题目来源：http://codeforces.com/group/aUVPeyEnI2/contest/229510
时间限制：2s
空间限制：256MB
题目大意：
给定一个凸多边形，有一种连接两个顶点可以将多边形分成两个非空的面积为整数的图形，询问这种线有多少条。
数据范围：
4 ≤ n ≤ 200 000
?109 ≤ xi, yi ≤ 109
样例：


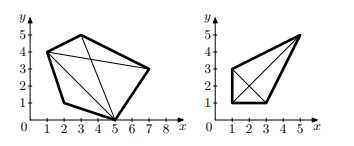
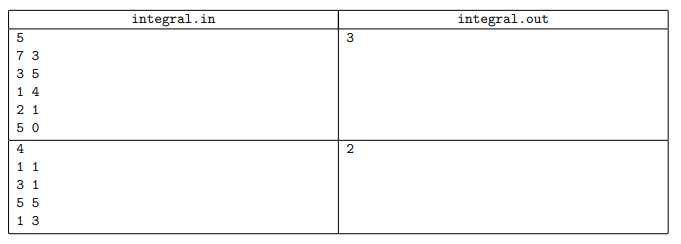
代码：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <cstdio>
#include <string>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#include <complex>
using namespace std;
typedef long long ll;
typedef long double db;
typedef pair<int,int> pii;
typedef vector<int> vi;
#define de(x) cout << #x << "=" << x << endl
#define rep(i,a,b) for(int i=a;i<(b);++i)
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define pi acos(-1.0)
#define mem0(a) memset(a,0,sizeof(a))
#define memf(b) memset(b,false,sizeof(b))
#define maxn 401010
int x[maxn],y[maxn];
int va[maxn],pre[maxn],p[maxn][3][3][3];
int across(int a,int b,int c,int d)
{
    return a*d-b*c;
}
int main()
{
    freopen("integral.in","r",stdin);
    freopen("integral.out","w",stdout);
    mem0(p);
    mem0(pre);
    int n;
    cin>>n;
    rep(i,1,n+1)
    {
        cin>>x[i]>>y[i];
        x[i]=x[i]&1;
        y[i]=y[i]&1;
        x[i+n]=x[i];
        y[i+n]=y[i];
    }
    rep(i,1,n<<1|1)
    {
        va[i]=across(x[i-1],y[i-1],x[i],y[i]);
        pre[i]=pre[i-1]+va[i];
    }
    if(pre[n+1]&1)
    {
        cout<<"0"<<endl;
        return 0;
    }
//  rep(i,1,n<<1|1)
//  {
//      printf("%5d",x[i]);
//  }
//  cout<<endl;
//  rep(i,1,n<<1|1)
//  {
//      printf("%5d",y[i]);
//  }
//  cout<<endl;
//  rep(i,1,n<<1|1)
//  {
//      printf("%5d",pre[i]);
//  }
//  cout<<endl;
    rep(i,1,n<<1|1)rep(a,0,2)rep(b,0,2)rep(c,0,2)
    {
        if(x[i]==a&&y[i]==b&&(pre[i]&1)==c)
        p[i][a][b][c]=p[i-1][a][b][c]+1;
        else
        p[i][a][b][c]=p[i-1][a][b][c];
    }
//  cout<<endl;
//  rep(i,1,n+1)
//  {
//      rep(a,0,2)
//      rep(b,0,2)
//      rep(c,0,2)
//      {
//          printf("%5d",p[i][a][b][c]);
//      }
//      cout<<endl;
//  }
//  cout<<endl;
    ll ans=0;
    rep(i,1,n+1)
    {
        int l=i+2,r=n+i-2;
        rep(a,0,2)rep(b,0,2)rep(c,0,2)
        {
            int t=((x[i]*b-y[i]*a+c-pre[i])&1);
            if(t==0)ans+=p[r][a][b][c]-p[l-1][a][b][c];
//          printf("%5d",ans);
        }
//      cout<<endl;
    }
    
    cout<<ans/2<<endl;
    return 0;
}