这是机器学习系列的第一篇文章。
本文将使用Python及scikit-learn的线性回归预测Google的股票走势。请千万别期望这个示例能够让你成为股票高手。下面按逐步介绍如何进行实践。
准备数据
本文使用的数据来自www.quandl.com网站。使用Python相应的quandl库就可以通过简单的几行代码获取到我们想要的数据。本文使用的是其中的免费数据。利用下面代码就可以拿到数据:
import quandl df = quandl.get(‘WIKI/GOOGL‘)
其中WIKI/GOOGL是数据集的ID,可以在网站查询到。不过我发现新版本的Quandl要求用户在其网站注册获取身份信息,然后利用身份信息才能读取数据。这里用到的WIKI/GOOGL数据集属于旧版本接口提供的数据,不需要提供身份信息。
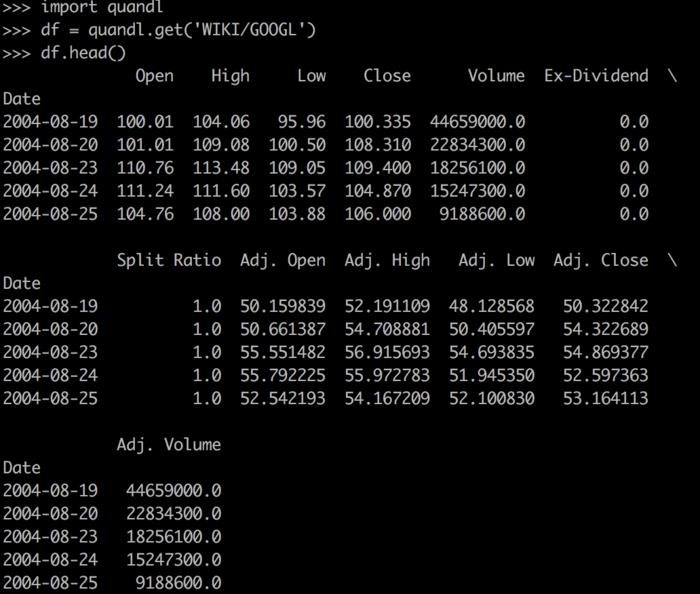
通过上面代码,我们把数据获取到,并存放在df变量中。默认地,Quandl获取到的数据以Pandas的DataFrame存储。因此你可以通过DataFrame的相关函数查看数据内容。如下图,使用print(df.head())可以打印表格数据的头几行内容。
预处理数据
从上面图片我们看到数据集提供了很多列字段,例如Open记录了股票开盘价、Close记录了收盘价、Volumn记录了当天的成交量。带Adj.前缀的数据应该是除权后的数据。
我们并不需要用到所有的字段,因为我们的目标是预测股票的走势,因此需要研究的对象是某一时刻的股票价格,这样的有比较性。所以我们以除权后的收盘价Adj. Close为研究对象来描述股票价格,也就是我们选择它作为将要被预测的变量。
接下来需要考虑关于什么变量跟股票价格有关。下面代码选取了几个可能影响Adj. Close变化的字段作为回归预测的特征,并对这些特征进行处理。详细步骤请阅读注释。
import math import numpy as np # 定义预测列变量,它存放研究对象的标签名 forecast_col = ‘Adj. Close‘ # 定义预测天数,这里设置为所有数据量长度的1% forecast_out = int(math.ceil(0.01*len(df))) # 只用到df中下面的几个字段 df = df[[‘Adj. Open‘, ‘Adj. High‘, ‘Adj. Low‘, ‘Adj. Close‘, ‘Adj. Volume‘]] # 构造两个新的列 # HL_PCT为股票最高价与最低价的变化百分比 df[‘HL_PCT‘] = (df[‘Adj. High‘] - df[‘Adj. Close‘]) / df[‘Adj. Close‘] * 100.0 # HL_PCT为股票收盘价与开盘价的变化百分比 df[‘PCT_change‘] = (df[‘Adj. Close‘] - df[‘Adj. Open‘]) / df[‘Adj. Open‘] * 100.0 # 下面为真正用到的特征字段 df = df[[‘Adj. Close‘, ‘HL_PCT‘, ‘PCT_change‘, ‘Adj. Volume‘]] # 因为scikit-learn并不会处理空数据,需要把为空的数据都设置为一个比较难出现的值,这里取-9999, df.fillna(-99999, inplace=True) # 用label代表该字段,是预测结果 # 通过让与Adj. Close列的数据往前移动1%行来表示 df[‘label‘] = df[forecast_col].shift(-forecast_out) # 最后生成真正在模型中使用的数据X和y和预测时用到的数据数据X_lately X = np.array(df.drop([‘label‘], 1)) # TODO 此处尚有疑问 X = preprocessing.scale(X) # 上面生成label列时留下的最后1%行的数据,这些行并没有label数据,因此我们可以拿他们作为预测时用到的输入数据 X_lately = X[-forecast_out:] X = X[:-forecast_out] # 抛弃label列中为空的那些行 df.dropna(inplace=True) y = np.array(df[‘label‘])
上面代码难点在理解label列的是如何生成的以及有什么用。实际上这一列的第i个元素都是Adj. Close列的第i + forecast_out个元素。我想尝试用简单文字描述:这列的每个数据是真实统计中的未来forecast_out天的收盘价。利用这一列的数据作为线性回归模型的监督标准,让模型学习出规律,然后我们才能用之预测结果。
另外X = preprocessing.scale(X)这行代码对X的数据进行规范化处理,让X的数据服从正态分布。(PS. 但是,我发现这种处理让X的数据都发生了变化,因此无法理解这样做的原因,以及为什么不会影响模型学习的结果。有知道答案的麻烦留言告告知。)
线性回归
上面我们已经准备好了数据。可以开始构建线性回归模型,并让用数据训练它。
# scikit-learn从0.2版本开始废弃cross_validation,改用model_selection from sklearn import preprocessing, model_selection, svm from sklearn.linear_model import LinearRegression # 开始前,先X和y把数据分成两部分,一部分用来训练,一部分用来测试 X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.2) # 生成scikit-learn的线性回归对象 clf = LinearRegression(n_jobs=-1) # 开始训练 clf.fit(X_train, y_train) # 用测试数据评估准确性 accuracy = clf.score(X_test, y_test) # 进行预测 forecast_set = clf.predict(X_lately) print(forecast_set, accuracy)
上述几行代码就是使用scikit-learn进行线性回归的训练和预测过程。我们可以通过测试数据计算模型的准确性accuracy,并且通过向模型提供X_lately计算预测结果forecast_set。
我运行得到的结果如下:
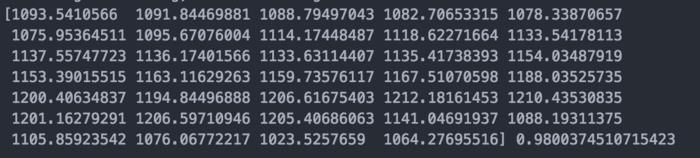
需要注意到的这个准确性accuracy并不表示模型预测100天的数据有97天是正确的。它表示的是线性模型能够描述统计数据的信息的一个统计概念。在后续的文章我可能会对这个变量进行一些讨论。
绘制走势
最后我们使用matplotlib让数据可视化话。详细步骤看代码注释。
import matplotlib.pyplot as plt
from matplotlib import style
import datetime
# 修改matplotlib样式
style.use(‘ggplot‘)
one_day = 86400
# 在df中新建Forecast列,用于存放预测结果的数据
df[‘Forecast‘] = np.nan
# 取df最后一行的时间索引
last_date = df.iloc[-1].name
last_unix = last_date.timestamp()
next_unix = last_unix + one_day
# 遍历预测结果,用它往df追加行
# 这些行除了Forecast字段,其他都设为np.nan
for i in forecast_set:
next_date = datetime.datetime.fromtimestamp(next_unix)
next_unix += one_day
# [np.nan for _ in range(len(df.columns) - 1)]生成不包含Forecast字段的列表
# 而[i]是只包含Forecast值的列表
# 上述两个列表拼接在一起就组成了新行,按日期追加到df的下面
df.loc[next_date] = [np.nan for _ in range(len(df.columns) - 1)] + [i]
# 开始绘图
df[‘Adj. Close‘].plot()
df[‘Forecast‘].plot()
plt.legend(loc=4)
plt.xlabel(‘Date‘)
plt.ylabel(‘Price‘)
plt.show()
运行代码可以得到下图。
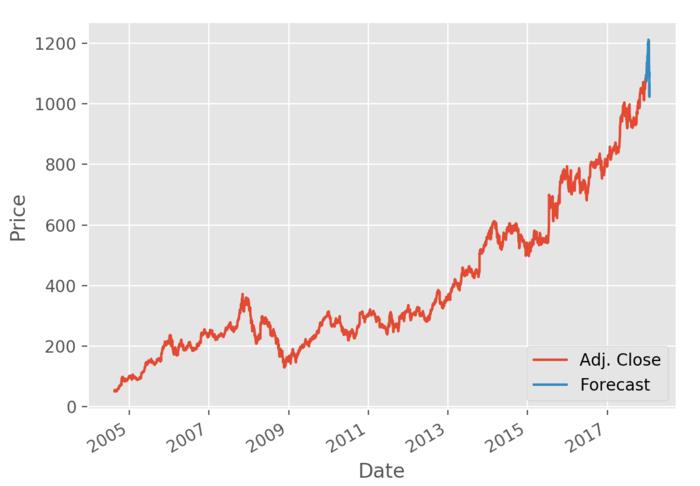
上图红色部分为采集到的已有数据,蓝色部分为预测数据。
点击这里查看完整代码。
本文来自同步博客
