主席树

Posted 2021-01-10 ve-2021

主席树

【前言】

Q：主席树是啥啊？

A：可持久化线段树。

Q：线段树又是啥呢？

A：二叉树的一种，每个节点都是一个区间。优秀的数据结构，代码实现戳这里。

Q：那可持久化是啥呀？

A：就是保存了这个数据结构的所有历史版本，且并不是每更新一个数据都要建树，而是能利用每次修改的不同版本之间的共同数据以减少时间和空间的消耗。

听起来好棒棒的样子QAQ_

以下内容来自这里和这里，由sharpland加以整合，而ve则是站在巨人的肩膀上学习。

【经典问题一】

输入n个数字组成的序列，询问序列中区间[l, r]上面的第K大的元素。其中第K大定义为：将区间[l, r]按升序排列后的第K个元素。

线段树可以询问最大最小值，但是第k大……裸线段树有点搞不定啊。

（1）    询问整个序列的第k大。

裸裸的线段树就能搞定啦。对值域建线段树，每个节点记录区间包含的元素个数，如果左边元素的个数sum >= k,地柜查找左子树第k大，否则递归查找右子树第k-sum大，直到返回叶子的值。

（2）考虑区间[l,r]的第k大

·   我们可以考虑求出[1,l-1]的第k大，再求出[1,r]的第k大，对这两棵线段树进行相减，得到的是相当于插入了[l,r]的线段树。注意这里利用区间相减的性质，实际上是用两棵不同历史版本的线段树进行相减：一棵是插入到第l-1个元素的旧树，另一棵是插入到第r元素的新树。

• 相减之后得到的相当于只插入了原序列中[l,r]元素的一棵记录了区间数字个数的线段树。直接对这棵线段树进行访问即可。
• 我们不能每对树中添一个元素都重建一棵树，那样未免也太不优秀，又要将它的历史版本存储，考虑将每个新增的节点新建就好。

【构造主席树】

我们可以先为“空前缀”建立一棵“空线段树”，里面的权值全是零。然后依次为每一个前缀建立线段树，与前一棵树相同的区间直接接到前一棵树的对应节点上，不同的部分再申请新的结点。

 

 

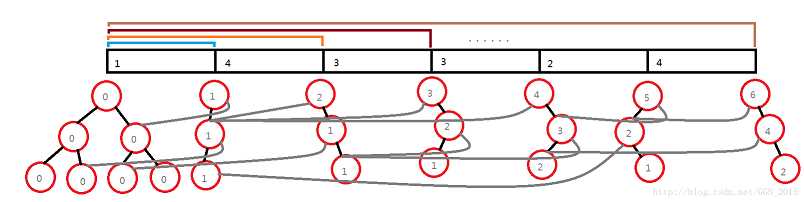
【经典问题二】

如何修改区间第k大呀？？？

• 前面我们提到前缀形式建线段树，如果能求出对于值域中的每个前缀都建一棵树的话，那真是太美妙了，MLE真的是太美妙了，于是我们想到了只新建新更新的节点。其实关于前缀和，我们实在是有一个很强大的数据结构呀——树状数组。
• 又是树状数组又是线段树感觉建树的时候不是很优秀啊……我们可以对于初始序列，按照无修改的方式建n棵线段树并且建好后不再修改，然后在另n棵空树上维护前缀和，两者加起来就得到了支持修改的并且插入了原序列[l,r]元素的线段树，对于它进行询问即可。

【简单例题】来自TonyFang良心出题人orz

poj2104/hdu2665

赤果果的板子，给出长度为n的序列，m个询问[l,r]之间的第k大值。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 using namespace std;
 5 const int maxs = 1e6+5;
 6 struct node {int a,b,l,r,sum;}tree[maxs*2];
 7 int a[maxs],b[maxs],root[maxs];
 8 int n,m,cnt,root_;
 9 inline void build(int &pos,int a,int b){
10     pos = ++cnt;
11     tree[pos].a = a;
12     tree[pos].b = b;
13     if(a==b) return;
14     int mid = a+b >> 1;
15     build(tree[pos].l,a,mid);
16     build(tree[pos].r,mid+1,b);
17 }
18 inline void insert(int pre,int &pos){
19     pos = ++cnt;
20     tree[pos].l = tree[pre].l;
21     tree[pos].r = tree[pre].r;
22     tree[pos].a = tree[pre].a;
23     tree[pos].b = tree[pre].b;
24     tree[pos].sum = tree[pre].sum + 1;
25     if(tree[pos].a == tree[pos].b) return;
26     int  mid = tree[pos].a + tree[pos].b >>1;
27     if(mid >= root_) insert(tree[pre].l,tree[pos].l);
28     else insert(tree[pre].r,tree[pos].r);
29 }
30 int query(int pre,int pos,int k){
31     if(tree[pos].l==tree[pos].r) return b[tree[pos].a];
32     int dt = tree[tree[pos].l].sum - tree[tree[pre].l].sum;
33     if(dt>=k) return query(tree[pre].l,tree[pos].l,k);
34     else return query(tree[pre].r,tree[pos].r,k-dt); 
35 }
36 int main(){
37     scanf("%d %d",&n,&m);
38     for(int i = 1;i <= n;b[i]=a[i],++i) scanf("%d",&a[i]);
39     sort(b+1,b+n+1);
40     build(root[0],1,n);
41     for(int i = 1;i <= n; ++i){
42         root_ = lower_bound(b+1,b+n+1,a[i]) - b;
43         insert(root[i-1],root[i]);
44     }
45     for(int i = 1;i <= m; ++i){
46         int l,r,k;
47         scanf("%d%d%d",&l,&r,&k);
48         printf("%d
",query(root[l-1],root[r],k));
49     }
50     return 0;
51 } 

View Code

上面这个板子很不优秀

hdu2665它光荣的T掉了，又码了一个，stl与手写的利与弊

两个板子在poj上测得的时间都差不多，但是在hdu上，下面这个就漂亮的满分，而上面的那个呀......光荣TLE了呜呜呜呜呜呜呜，时间近十倍

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<vector> 
 6 using namespace std;
 7 const int M = 2000010;
 8 const int N = 100010;
 9 int n, a[N], m;
10 int ch[M][2], sz=0, rt[N], s[M];
11 vector<int> ps;
12 vector<int>::iterator it;
13 int fps[N], mx;
14  
15 inline void add(int &root, int oldrt, int l, int r, int t) {
16     root=++sz;
17     ch[root][0] = ch[root][1] = 0;
18     s[root]=s[oldrt]+1;
19     if(l == r) return;
20     int mid=l+r>>1;
21     if(t>mid) add(ch[root][1], ch[oldrt][1], mid+1, r, t), ch[root][0] = ch[oldrt][0];
22     else add(ch[root][0], ch[oldrt][0], l, mid, t), ch[root][1] = ch[oldrt][1];
23 }
24  
25 inline int query(int rtl, int rtr, int l, int r, int k) {
26     if(l == r) return l;
27     int t = s[ch[rtr][0]] - s[ch[rtl][0]];
28     int mid = l+r>>1;
29     if(k <= t) return query(ch[rtl][0], ch[rtr][0], l, mid, k);
30     else return query(ch[rtl][1], ch[rtr][1], mid+1, r, k-t);
31 }
32  
33 int main() {
34 //    int T;
35 //    scanf("%d", &T);
36 //    while(T--) {
37         scanf("%d%d", &n, &m);
38         ps.clear(); sz=0;
39         memset(ch, 0, sizeof(ch));
40         memset(rt, 0, sizeof(rt));
41         memset(s, 0, sizeof(s));
42         for (int i=1; i<=n; ++i) {
43             scanf("%d", &a[i]);
44             ps.push_back(a[i]);
45         }
46         sort(ps.begin(), ps.end());
47         it = unique(ps.begin(), ps.end());
48         ps.erase(it, ps.end());
49         mx = -1;
50         for (int i=1; i<=n; ++i) {
51             int t = lower_bound(ps.begin(), ps.end(), a[i]) - ps.begin() + 1;
52             fps[t] = a[i];
53             a[i] = t;
54             mx = max(mx, t);
55         }
56         for (int i=1; i<=n; ++i)
57             add(rt[i], rt[i-1], 1, mx, a[i]);
58         while(m--) {
59             int l, r, k;
60             scanf("%d%d%d", &l, &r, &k);
61             printf("%d
", fps[query(rt[l-1], rt[r], 1, mx, k)]);
62         }
63 //    }
64     return 0;
65 }

View Code

 题没写完，弃坑待填......未完待续