一图看完整个数学脉络

Posted 2023-03-04 卓晴

一图看完数学全貌

• The Map of Mathematics

 

01 数学地图

---

一、前言

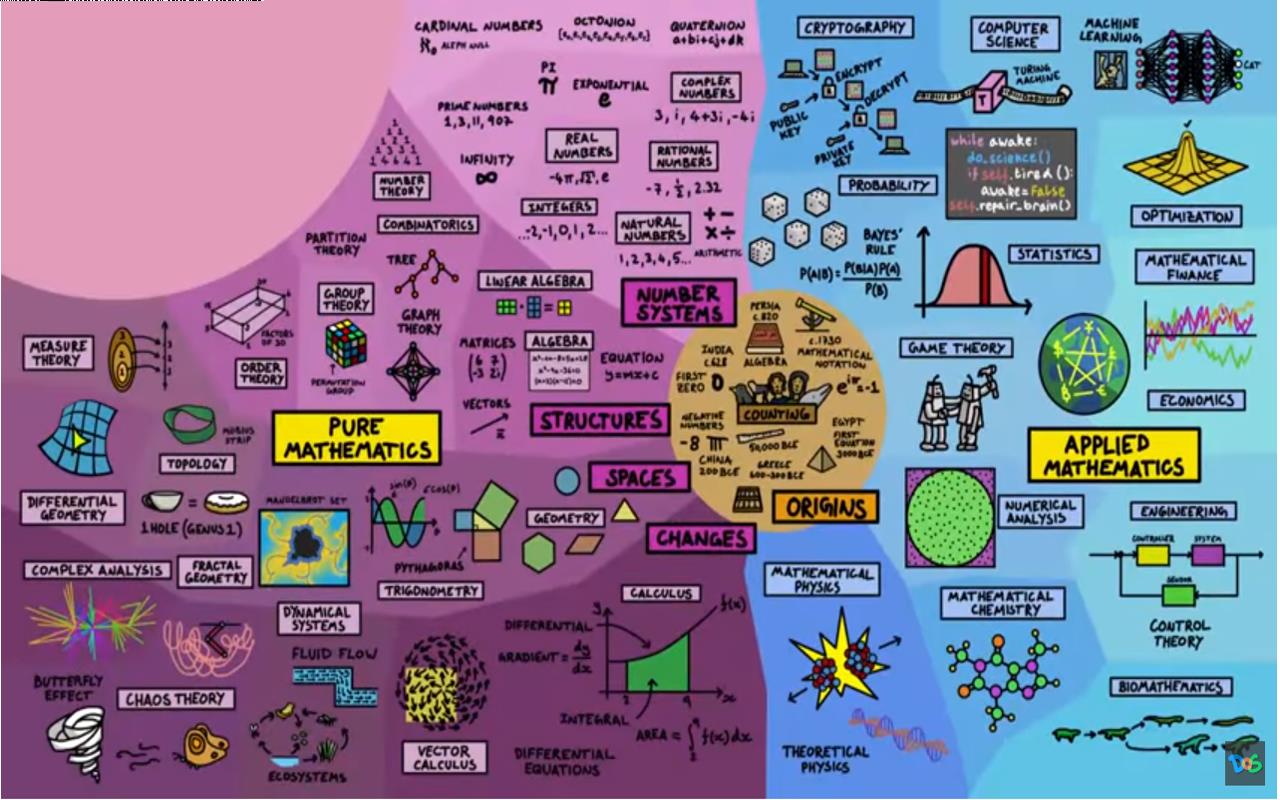
  我们在学校学习的数学并不能完全展示出数学所有领域， 实际上我们只能瞥见它的一个角落。 但数学作为一个整体是一门庞大而奇妙的学科， 下面内容是向你展示它的所有令人惊奇的东西。

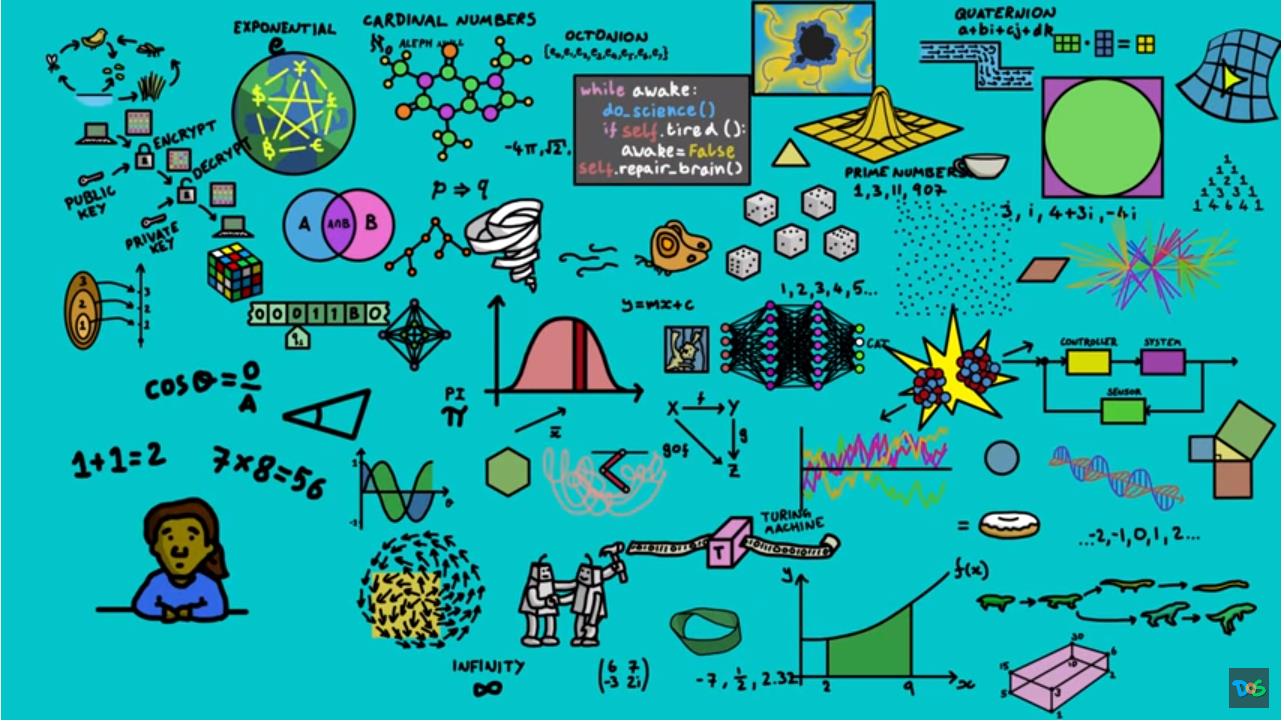
▲ 图1.1.1 数学地图

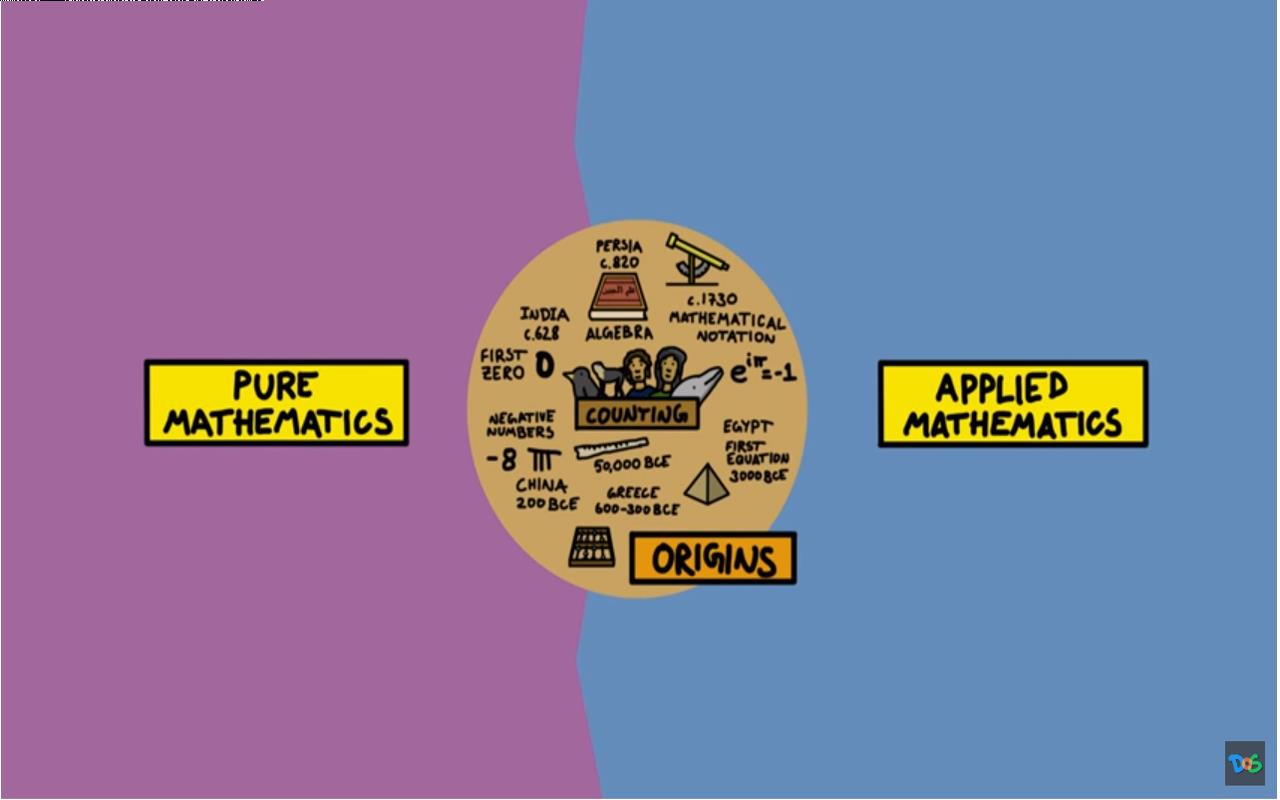
二、数学起源

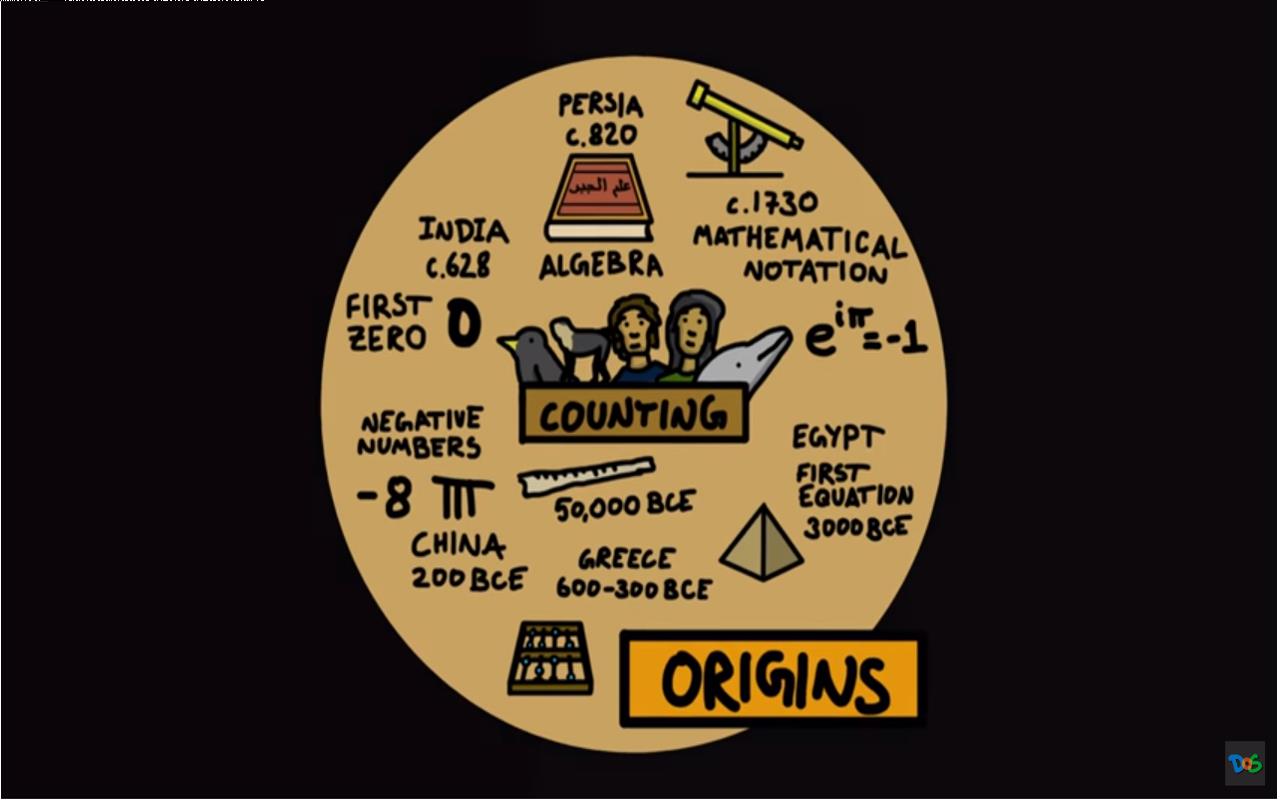
  我们将从数学的起源说起。 人类的数学起源于对物体的个数进行计数。 事实上，数数不仅仅是人类的能力，其他动物也能数数， 你说惊喜不惊喜？  人类可以数数的证据可以追溯到史前时代，比如，在骨骼化石上发现用于计数用的刻画标记。  经过漫长的演变， 人类数学逐步升级，出现了更加复杂数学能力： 埃及人发明了第一个方程，古希腊人在几何和命理学等许多领域取得了长足进步，中国发明了负数概念。  零作为数字首先在印度使用。  当伊斯兰教进入她的黄金时代时，波斯数学家取得了更大的进步，并写出了第一本关于代数的书。  然后数学与科学一起在文艺复兴时期得到蓬勃发展。

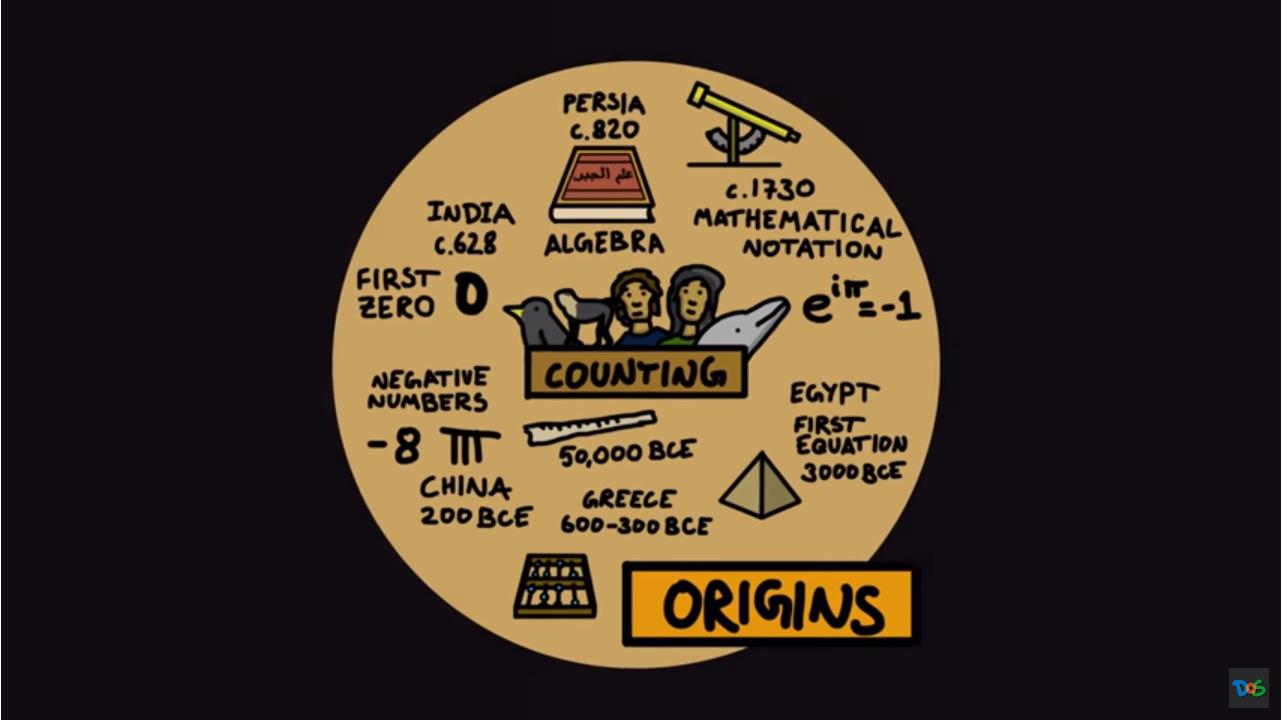
▲ 图1.2.1 数学的起源

三、数学分类

  当然，数学发展史比刚才说的要丰富的多，不过还是让我们把目光集中在现代数学上。  现代数学可以大致分为两个领域，纯数学：为数学本身而研究数学，以及应用数学：帮助解决一些现实世界问题的数学。 它们之间具有很多交叉。  事实上，在历史上很多人纯粹出于好奇心或者某种美感进入数学领域， 在忽明忽暗的探索中拾取着一个个令人惊奇的收获， 伴随而来的是一大堆他们创造的新的数学，这些数学是那么的完美，那么的迷人，但要问它们有什么实际用途，抱歉， 也许当你想问这个问题时已经说明你可能已经来到了错误的地方。 

▲ 图1.3.1 理论数学
  也许在一百年后，有人会在物理学或计算机科学的前沿碰到一些问题，他们会发现纯数学中一些古老理论正是他们所需要的工具， 可以帮助他们解决现实世界问题！ 这的确太棒了！  在过去的几个世纪里，这种事情发生了很多次。 有趣的是，如此抽象的数学往往最终变得非常有用。 这里需要提一下，纯数学本身仍然是一件非常有价值的事情，因为它那复杂而深邃的面纱背后，就透露出真正的完美和优雅，几乎像艺术一样， 它那动人之处只可意会，不可言传。  好吧，关于数学夸夸其谈到此为止，让我们开始谈谈数学这两个分支吧。

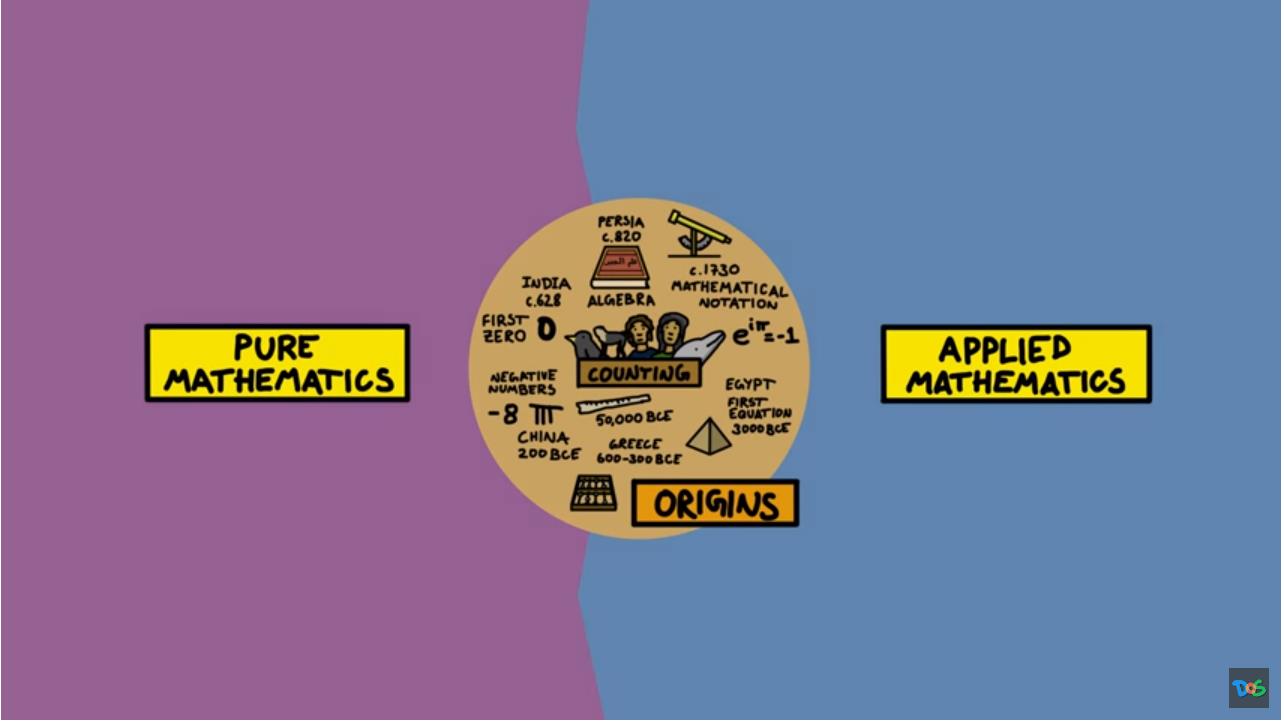
▲ 图1.3.2 理论数学与应用数学

四、理论数学

  纯数学也分为几个部分组成。 数字的研究从自然数开始，你可以用算术运算对它们进行操作。  除了自然数之外，我们还可以查看一下其它的数字类型。 例如包含负整数、分数等有理数、包括 pi 等无限小数的实数，然后是复数和一大堆其他数字。 

  有些数字具有特殊的性质，例如质数、圆周率或指数。  不同数系也各自具有一些特殊性质。 例如，尽管整数和实数都是无限的，但实数比整数多。 所以一些无穷大比其他无穷大更大， 这听起来十分绕口。 

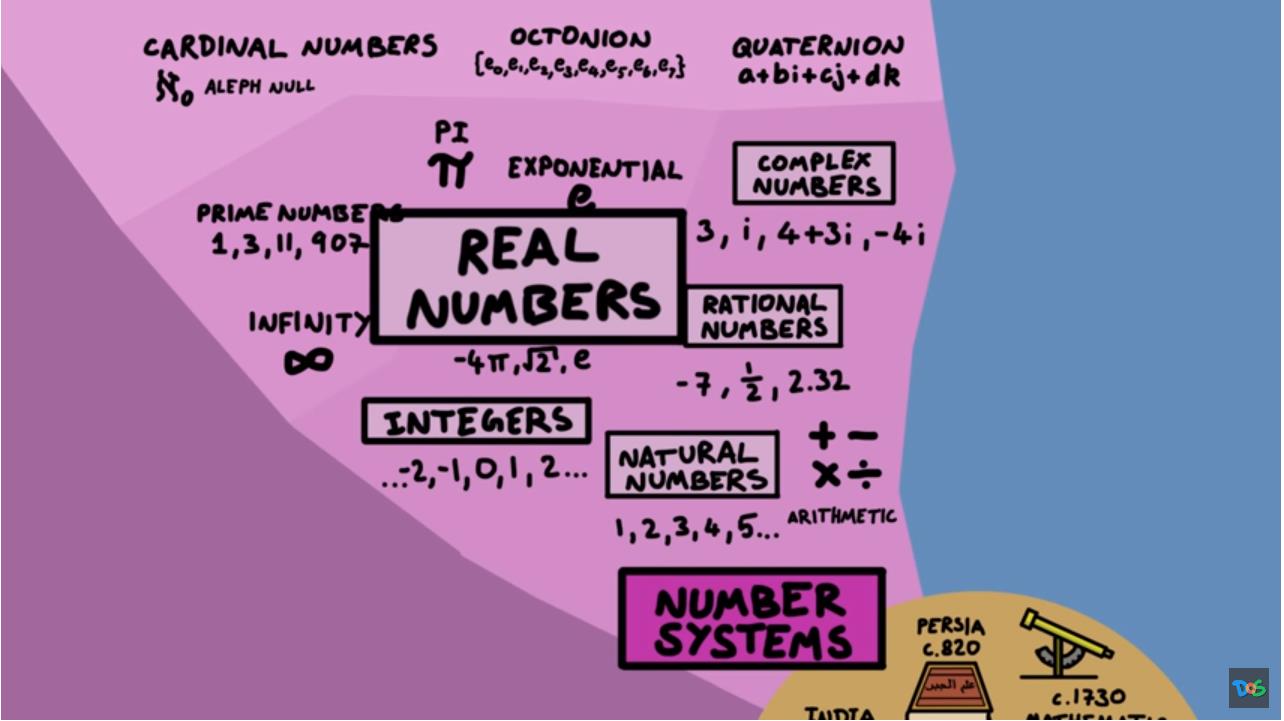
▲ 图1.4.1 不同数字分类和特性
  代数将数字以变量进行表示， 并将变量组成方程式。  代数数学中包含如何操作这些方程式的规则。 在这里你还会发现向量和矩阵，它们是多维数字，它们之间的关系规则在线性代数中得到了体现。

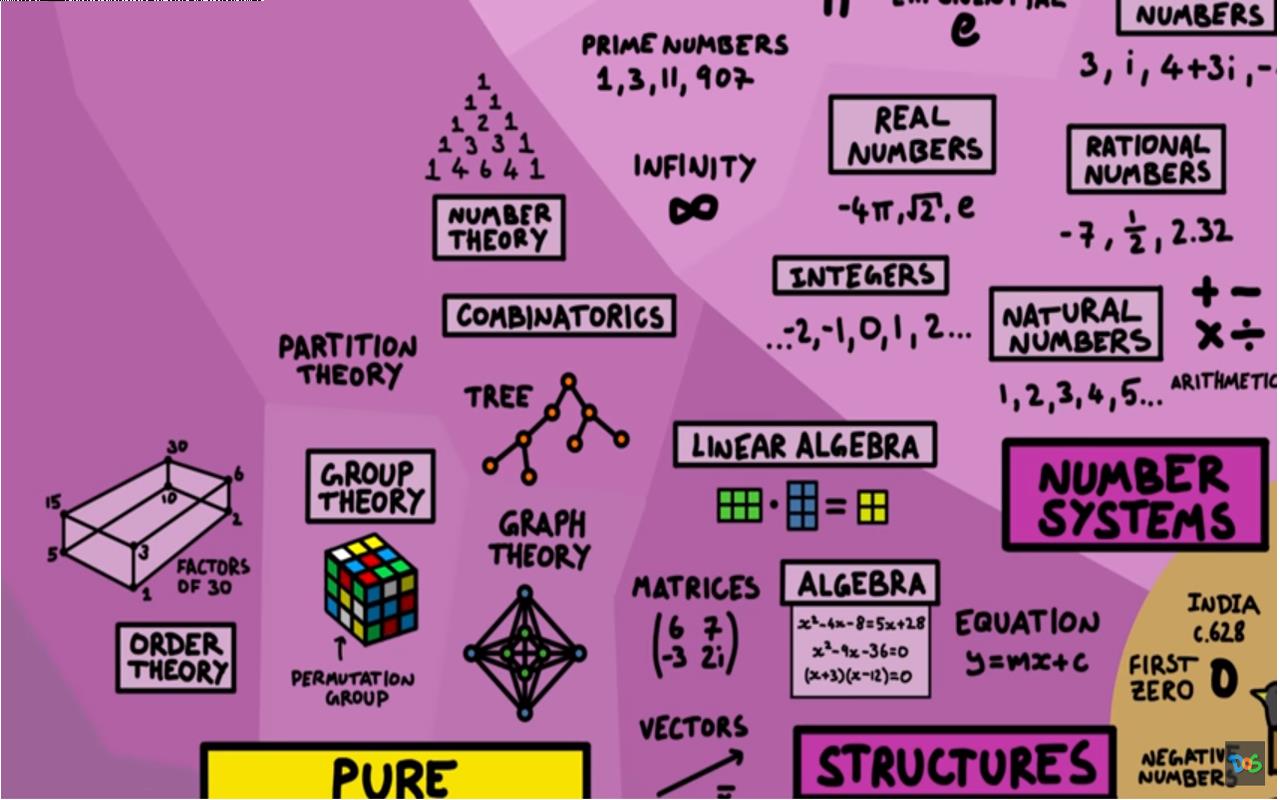
  数论研究了上一节关于数字的一切特征，例如素数的性质。  组合数学着眼于某些结构的属性，例如树、图和其它可以计算的离散对象组成的东西。  群论着眼于群体中相互关联的对象。 一个熟悉的例子是魔方，它是置换群的一个例子。  排序理论研究如何按照一定的规则排列物体，比如某物的数量如何大于另一物。  自然数是有序对象集的一个例子，任何具有双向关系的事物都可以排序。

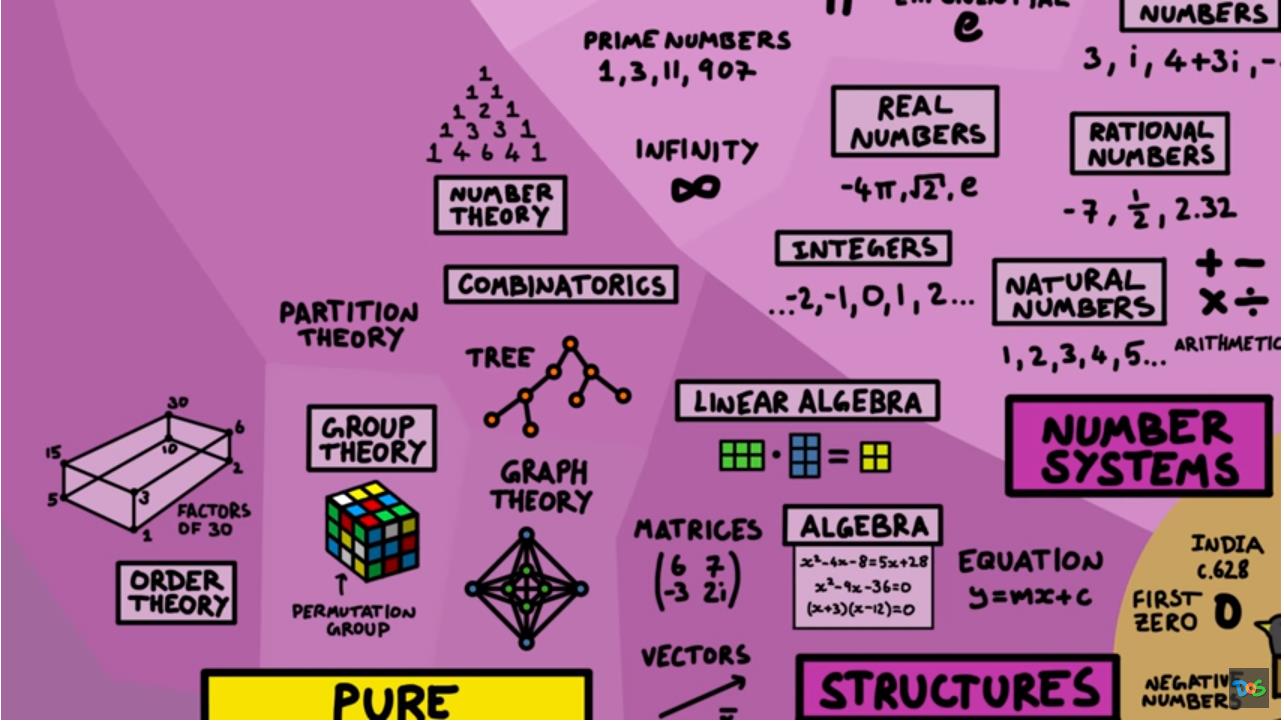
▲ 图1.4.2 数字结构与数论
  纯数学的另一部分着眼于形状以及它们在空间中的行为方式。 起源于包括毕达哥拉斯在内的几何学， 这些数学内容与我们在中学中学习的三角学有相同之处。  此外还有一些有趣的东西，比如分形几何，它是尺度不变的数学模式，这意味着你可以永远放大它们，而且看起来总是一样的。  拓扑学着眼于空间的不同属性，可以利用这些属不断地使它们变形的同时，又不撕裂或粘合它们。  例如，莫比乌斯带只有一个表面和一条边。  从拓扑学上讲咖啡杯和甜甜圈是同一件事。

  测度论是一种将值分配给空间或将数字和空间联系在一起的集合方法。  微分几何研究的是曲面上形状的性质，例如三角形在曲面上有不同的角度， 这将我们带到下一节，即数学中的变化。

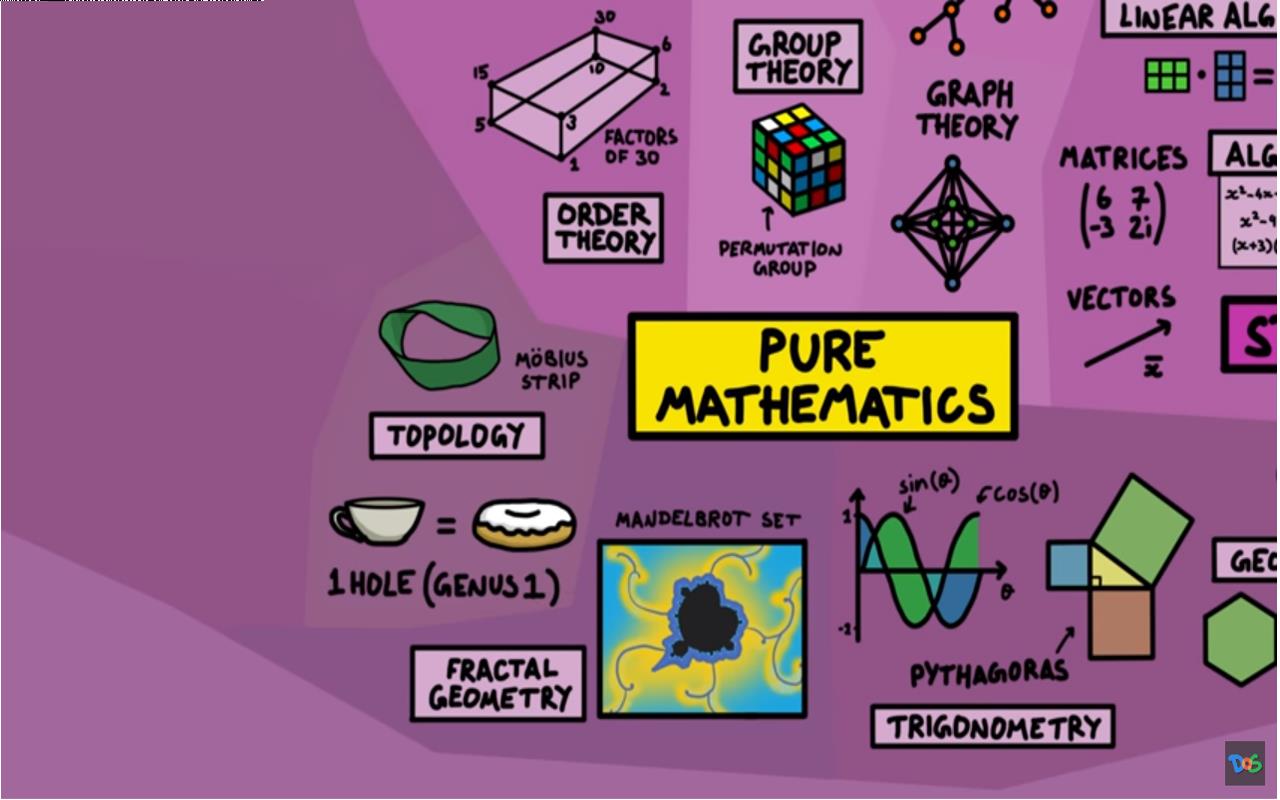
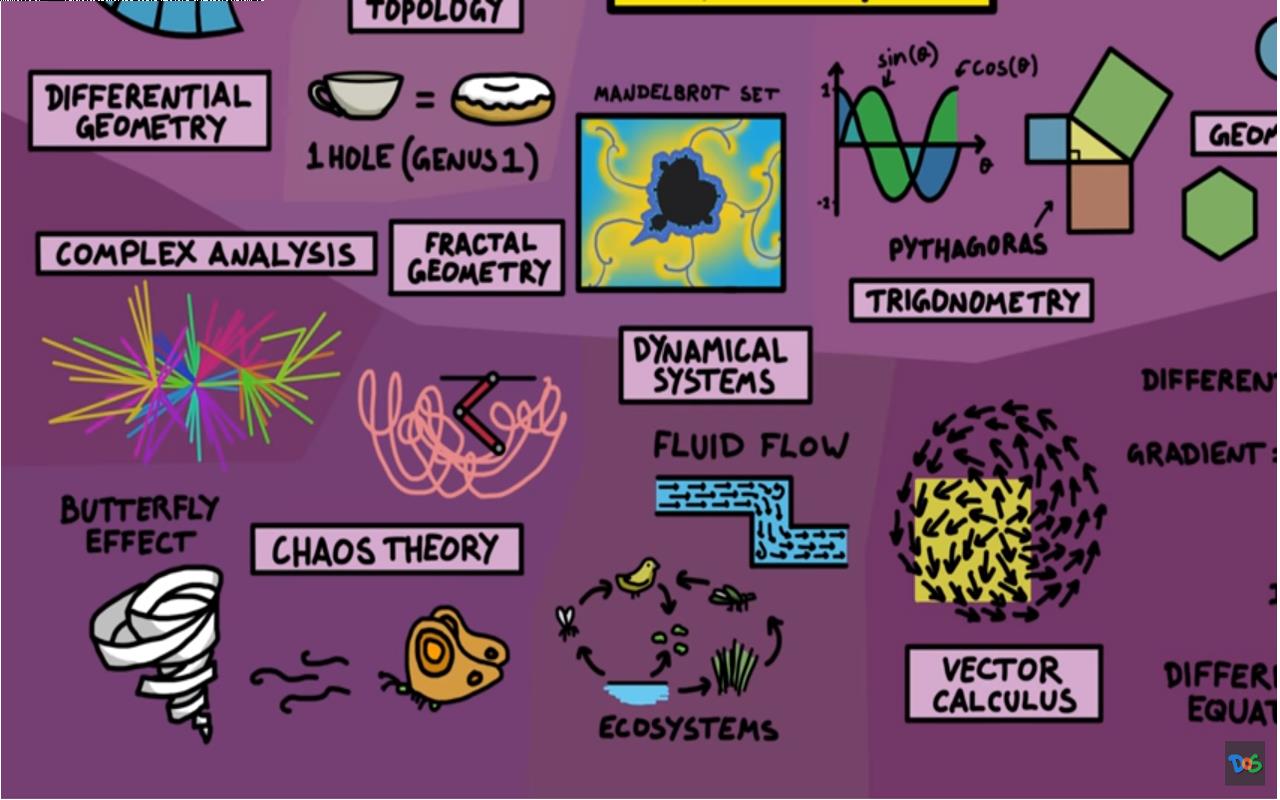
  变化研究主要包括微积分，涉及积分和微分，它们着眼于函数曲线包围的区域面积或函数导数等概念。 向量微积分对向量也有同样的概念。  在这里，我们还发现了许多其它领域，例如动态系统，它分析那些状态随时间演变的系统，例如流体流动或具有反馈回路的系统，例如生态系统。 混沌理论研究对初始条件非常敏感的动态系统。  最后，复数分析着眼于包含复数变量的函数的特性。

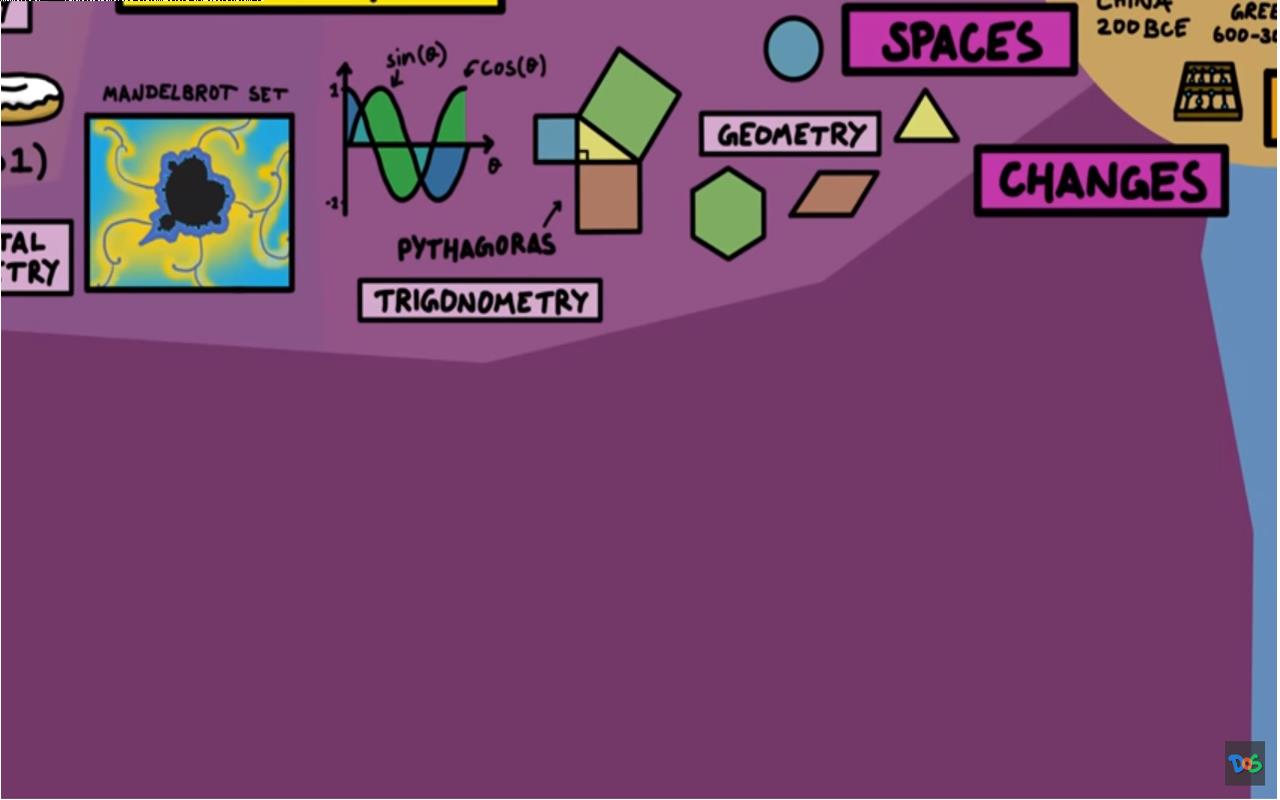
▲ 图1.4.3 空间几何与微积分

五、应用数学

  下面在讨论一下应用数学。 这方面值得一提的是，应用数学内容包含有比这个二维图更加复杂的相互关联。 事实上，这张地图应该看起来更像是一张网络， 将所有不同主题联系在一起，但在二维平面上只能做这么多，所以尽可能地把它们布置好。 
  下面先从物理学开始，它在某种程度上几乎使用了纯数学中的的所有内容。 理论物理与纯数学有着非常密切的关系。  数学也用于其他自然科学，包括化学和生物等，这些自然科学研究从分子建模到进化生物学等广泛内容。

  数学也广泛用于工程，自古埃及和古巴比伦时代以来，建造工程中需要大量的数学知识。  非常复杂的大型系统中，如飞机或电网，使用控制理论的数学方法来设计和分析这类动态系统。  数值分析作为一种数学工具，常用于数学模型过于复杂而无法完全求解的地方， 通过大量简化后的近似计算，将结果组合在一起获得良好的近似答案。  比如把一个圆放在一个正方形里面，向它扔飞镖，然后比较圆和正方形部分飞镖的数量，就可以近似得到圆周率的值。 但在现实世界中，数值分析通常在巨型计算机上完成的。  博弈论着眼于给定一套游戏规则情形下理性玩家如何获得最佳选择，通常假设参与游戏的各个玩家都是很聪明时，博弈论常常被用于经济学，心理学和生物学等。 

▲ 图1.5.1 博弈论与随机统计

  概率论是对随机事件的研究，例如掷硬币或骰子。 统计学是对随机过程产生的大量集合或数据进行分析研究， 在金融领域得到广泛应用， 指导建立金融系统模型并由产生预测并可获得更多利润。 

  与此相关的还包括优化，帮你在一组许多不同的选项或约束中计算出最佳选择，最终是将实际问题抽象函数， 通过数学方法获得该函数的最高点或最低点。 优化问题是我们人类的第二天性，在社会生活中我们无时无刻都在做这些问题：试图获得高的金钱收益，或者试图以某种方式将幸福最大化。 

  另一个与纯数学密切相关的领域是计算机科学，计算机科学的规则实际上是从纯数学中推导出来的，在可编程计算机被制造之前人们就已经制定出一些算法。 

  机器学习，创建了智能计算机系统的， 它使用了数学中的许多领域，如线性代数、优化、微积分和概率论。 
  最后，密码学理论对计算非常重要，它使用了很多纯数学，如组合数学和数论。 到此为止我们这种数学地图涵盖了纯数学和应用数学的主要部分，  在结束讨论之前，我们在看一下数学基本属性。

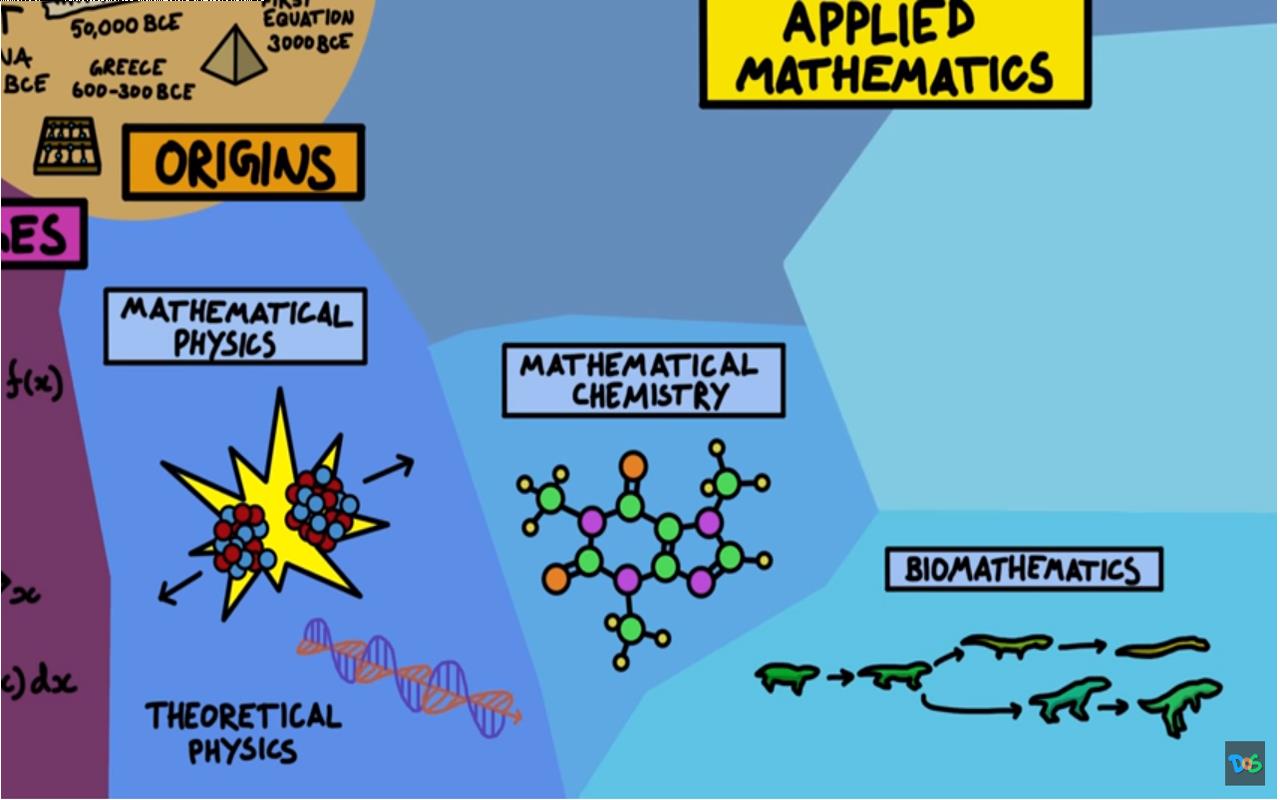
▲ 图1.5.2 应用数学的一部分

六、数学基础

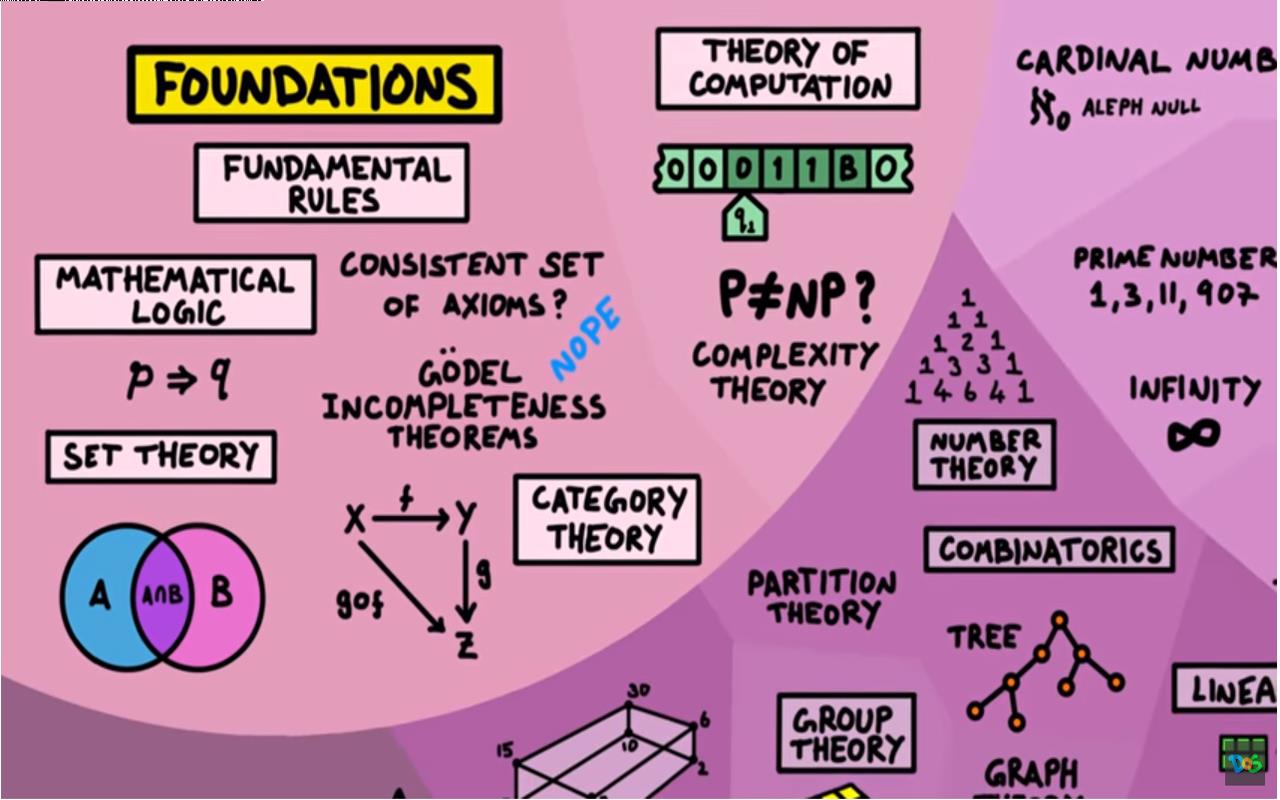
  数学性质领域试图解决数学本身的属性，并探究所有数学规则的基础是什么？ 否有一套完整的基本规则？ 这些基本规则称为公理，所有数学都来自它。 而我们能否证明它具有一致性和完备性？  数理逻辑、集合论和范畴论试图回答这个问题。 数理逻辑中一个著名的结果是哥德尔不完备性定理，对大多数人来说，这意味着数学没有完备且一致的公理集合，这看起来数学很像我们人类那样总是或多或少具有某种缺点， 这很奇怪是不是？ 数学可以很好地解释了宇宙中的这么多东西， 人类造出来的数学为什么能这样？ 这的确令人感到很神奇。   我们还有计算理论，它着眼于不同的计算模型以及它们解决问题的效率，包含有复杂性理论，它着眼于什么是可计算的和不可计算的， 以及需要多少内存和时间。 其中描述复杂最基本的概念就是所谓的数量级。

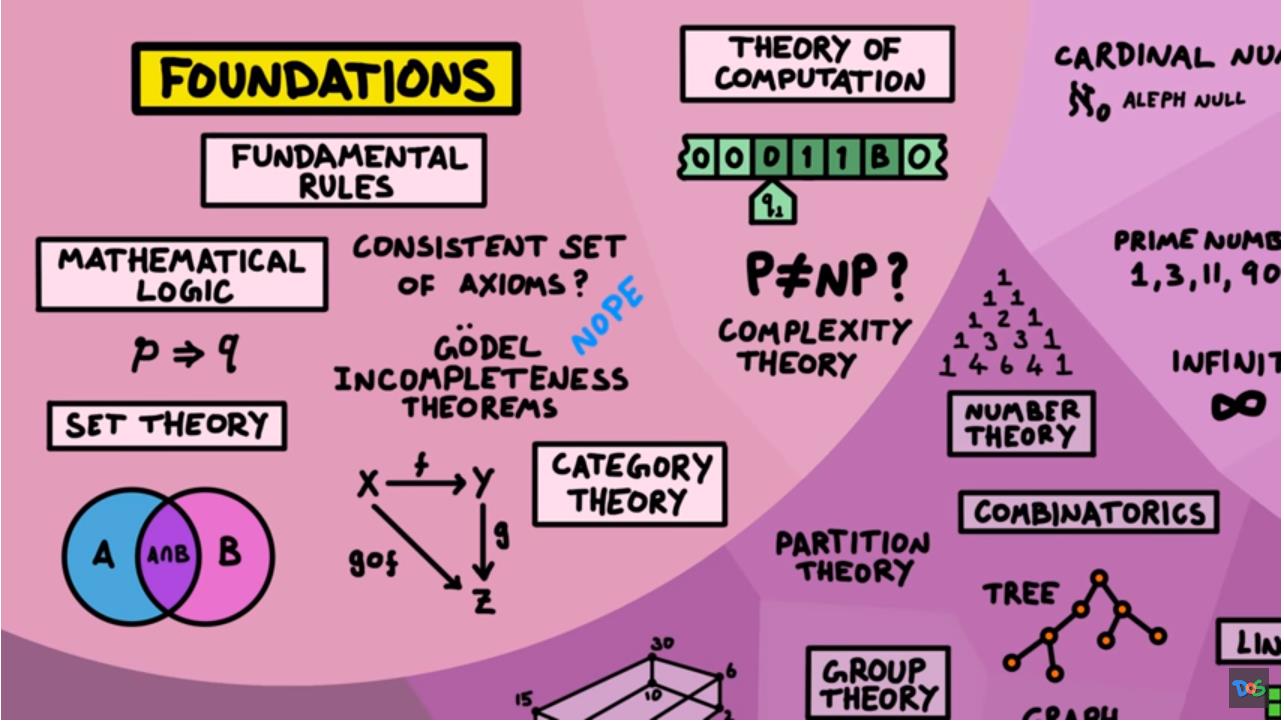
▲ 图1.6.1 数学基础

七、后记

  这就是数学的地图全貌。 关于学习数学中我最喜欢的事情， 就是当你感觉一个东西看起来如此令人困惑， 但突然在某一时刻你的大脑突然开窍， 有了醍醐灌顶的感觉，一切都变得清晰明朗起来。 仿佛经历了一次顿悟，一刹那数学概念变得井井有条。 这种感觉让我在学习数学中心满意足， 不停地深入思考了数学的某些部分，好像我瞥见了宇宙所有对称奇观背后基本原理。 

▲ 图1.7.1 数学地图完整版本

---

■ 相关文献链接:

• The Map of Mathematics

● 相关图表链接:

• 图1.1.1 数学地图
• 图1.2.1 数学的起源
• 图1.3.1 理论数学
• 图1.3.2 理论数学与应用数学
• 图1.4.1 不同数字分类和特性
• 图1.4.2 数字结构与数论
• 图1.4.3 空间几何与微积分
• 图1.5.1 博弈论与随机统计
• 图1.5.2 应用数学的一部分
• 图1.6.1 数学基础
• 图1.7.1 数学地图完整版本