数论板子大总结

Posted 2020-10-16

在这里，将有我迄今为止学过的所有数论。

1、素数筛——埃拉托斯特尼筛法

时间复杂度：O(nloglogn)
方法：用每个素数筛所有它的倍数
证明：略

    for (int i=2;i<=N;i++) is[i]=1;
    for (int i=2;i<=N;i++)
    if (is[i])
        for (int j=i*i;j<=2000;j+=i)
        is[j]=0;

2、素数筛——欧拉筛法

时间复杂度：O(n)
方法&证明：埃拉托斯特尼对于每个合数筛了很多遍，而欧拉对于每个合数只被自己的最小质因数所筛去

    memset(is,1,sizeof(is));
    for (int i=2;i<=100000;i++)
    {
    if (is[i]) prime[++cnt]=i;
    for (int j=1;j<=cnt && i*prime[j]<=100000;j++)
    {
        is[i*prime[j]]=0;
        if (i%prime[j]==0) break;
    }       
    }

3、欧拉函数

求[2,n)中与n互质的数的个数
//欧拉函数记做$\\Phi(n)$
性质：
$\\Phi(n)=\\Phi(P_1^{a_1})\\Phi(P_2^{a_2})\\Phi(P_3^{a_3})…\\Phi(P_s^{a_s})$
P为n的质因数，在n中a为其质因数的幂
定理：
(1)如果p是素数，那么$\\Phi(p)=p-1$ （逆定理成立）
(2)如果p是素数，那么$\\Phi(p^a)=p^a-p^{a-1}$
(3)设n和m互质，$\\Phi(nm)=\\Phi(n)\\Phi(m)$
(4)p为n的质因数，a为对应指数，$\\Phi(n)=n(1-1/p_1)(1-1/p_2)(1-1/p_3)…(1-1/p_s)$
推论：当n为奇数时，$\\Phi(2n)=\\Phi(n)$
(5)设n>2，那么$\\Phi(n)$是偶数
(6)设n为正整数，$\\sum_{d|n} \\phi(d) = n$

//求一个数的欧拉函数
ll phi(ll x)
{
    ll ans=x,c=x;
    for (int i=2;i<=c/i;i++)
    {
    if (c%i==0) ans=ans/i*(i-1);
    while(c%i==0) c/=i;
    }
    if (c>1) ans=ans/c*(c-1);
    return ans;
}
//求[1,n]的欧拉函数
void euler(ll n)
{
    ll cnt=0;
    memset(is,1,sizeof(is));
    is[1]=0;
    for (ll i=2;i<=n;i++)
    {
    if (is[i]) prime[++cnt]=i,phi[i]=i-1;
    for (int j=1;j<=cnt && prime[j]*i<=n;j++)
    {
        is[prime[j]*i]=0;
        if (i%prime[j]==0)
        {
        phi[i*prime[j]]=phi[i]*prime[j];
        break;
        }
        phi[i*prime[j]]=phi[i]*(prime[j]-1);
    }
    }
}

4、欧拉定理&费马小定理&乘法逆元

欧拉定理：对于任何两个互质的正整数a和m(m>1)，有$a^{\\Phi(m)}\\equiv1(mod m)$
费马小定理：当m是质数时，$a^{m-1}\\equiv1(mod m)$

5、欧几里得算法

//求a和b的最大公因数，记做gcd(a,b)
//（最小公倍数记做lcm(a,b)，显然lcm(a,b)=a*b/gcd(a,b)）
又名辗转相除法
原理：gcd(a,b)=gcd(b,a%b)
（详情请参见更相减损术）

6、扩展欧几里得算法

求解ax+by=gca(a,b)的x和y
显然这是一个不定方程，所以有多组解，而ex_gcd可以得出其中一组解，然后我们可以通过转换求出所有解
证明：

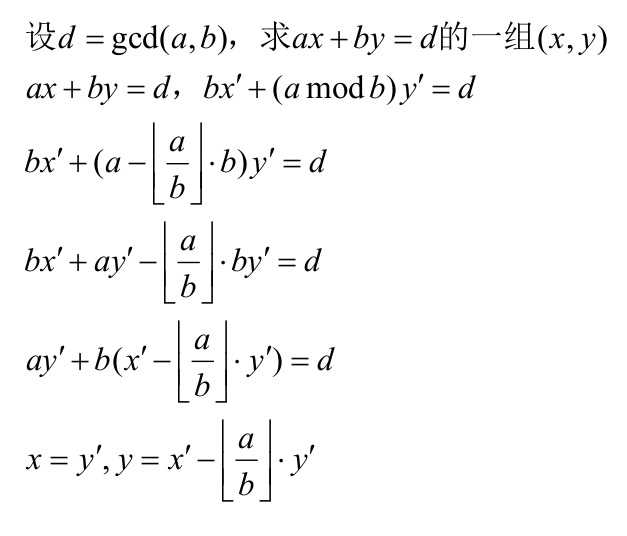
因为$ax+by=1$ $→$ $ax+by+ab-ab=1$ $→$ $a(x+b)+b(y+a)=1$
所以在求出一个可行解x之后,不断的把x+-b仍是该方程的一个解,利用这个性质可以求类似最小解的问题

void ex_gcd(ll a,ll b,ll &x,ll &y)
{
    if (!b)
    {
    x=1;
    y=0;
    return ;
    }
    ex_gcd(b,a%b,y,x);
    y-=a/b*x;
}

7、中国剩余定理

emm…证明太繁琐，附上百度百科的网址把
qwq

int CRT(int a[],int m[],int n)
{
    int M=1;
    int ans=0;
    for (int i=1;i<=n;i++)
    M*=m[i];
    for (int i=1;i<=n;i++)
    {
    int x,y;
    int Mi=M/m[i];
    exgcd(Mi,m[i],x,y);
    ans=(ans+Mi*x*a[i])%M;
    }
    if (ans<0) ans+=M;
    return ans;
}