Perfect Rectangle(完美矩形)

Posted 2021-01-09 shit

我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。

每个矩形用左下角的点和右上角的点的坐标来表示。例如， 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。

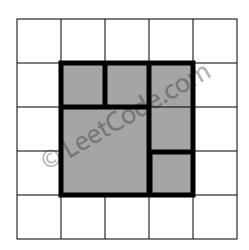
示例 1:

rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [3,2,4,4],
  [1,3,2,4],
  [2,3,3,4]
]

返回 true。5个矩形一起可以精确地覆盖一个矩形区域。

 

 

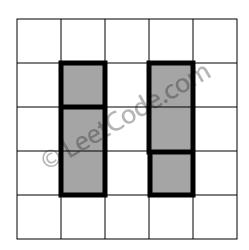
示例 2:

rectangles = [
  [1,1,2,3],
  [1,3,2,4],
  [3,1,4,2],
  [3,2,4,4]
]

返回 false。两个矩形之间有间隔，无法覆盖成一个矩形。

 

 

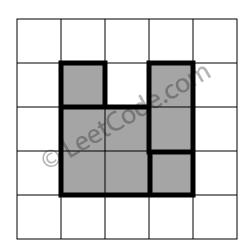
示例 3:

rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [1,3,2,4],
  [3,2,4,4]
]

返回 false。图形顶端留有间隔，无法覆盖成一个矩形。

 

 

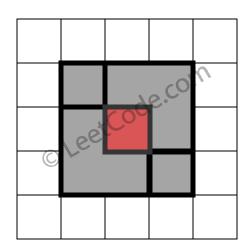
示例 4:

rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [1,3,2,4],
  [2,2,4,4]
]

返回 false。因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

这道题我在写前两个解法的时候还没ac通过，但是已经忍不住要写了。思路还是很清晰的，遍历矩形，算有没有重合，面积累加，最后看看总面积是不是最大范围的覆盖的矩形的面积。
第一遍暴力解法：

class Solution {
public:
    bool Cover(vector<int>& a, vector<int>&b)
    {
        if (min(a[0], a[2]) >= max(b[0], b[2]) || max(a[0], a[2]) <= min(b[0], b[2])
            || min(a[1], a[3]) >= max(b[1], b[3]) || max(a[1], a[3]) <= min(b[1], b[3]))
        {
            return false;
        }
        return true;
    }
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        int minx, miny, maxx, maxy;
        minx = miny = INT_MAX;
        maxx = maxy = INT_MIN;
        long long int sum = 0;
        for (int i = 0; i < rectangles.size();i++)
        {
            for (int r = 0; r < i;r++)
            {
                if (Cover(rectangles[i], rectangles[r]))
                {
                    return false;
                }
            }
            minx = min(minx, min(rectangles[i][0], rectangles[i][2]));
            miny = min(miny, min(rectangles[i][1], rectangles[i][3]));
            maxx = max(maxx, max(rectangles[i][0], rectangles[i][2]));
            maxy = max(maxy, max(rectangles[i][1], rectangles[i][3]));
            sum += abs((rectangles[i][0] - rectangles[i][2])*(rectangles[i][1] - rectangles[i][3]));
        }
        return sum == (maxx - minx)*(maxy - miny);
    }
};

果不其然挂了，测试最后两组都是3w+的数据量

第二遍：四叉树解法

class QuadNode
{
public:
    enum{
        quad_1,//四个象限
        quad_2,
        quad_3,
        quad_4,
        quad_count,
    };
    vector<vector<int>>* data;
    QuadNode* Children[quad_count];//孩子指针,数组大小为8
    QuadNode* Parent;//父节点指针
    typedef std::list<int> RecList;
    typedef std::list<int>::iterator RecListIter;
    RecList rectlist;//携带的参数  实体列表
    int quad;//在父节点中的象限
    int deep;//自己所在的层索引
    int minx,miny;
    int maxx,maxy;
    QuadNode(vector<vector<int>>* data, int x1, int x2, int y1, int y2, int dp, int qd)
    {
        minx = x1;
        maxx = x2;
        miny = y1;
        maxy = y2;
        deep = dp;
        quad = qd;
        Parent = NULL;
        this->data = data;
        memset(Children, 0, sizeof(Children));
    }
    ~QuadNode()
    {
        for (int i = 0; i < quad_count; i++)
        {
            if (Children[i])
            {
                delete Children[i];
                Children[i] = NULL;
            }
        }
        rectlist.clear();
    }
    QuadNode* GetDeepest(int index)
    {
        if (deep > 0)
        {
            //4个孩子都要创建
            for (int r = 0; r < QuadNode::quad_count; r++)
            {
                if (!Children[r])
                {
                    int ix = r == QuadNode::quad_1 || r == QuadNode::quad_3 ? minx : (minx + maxx) / 2;
                    int ax = r == QuadNode::quad_1 || r == QuadNode::quad_3 ? (minx + maxx) / 2 : maxx;

                    int iy = r == QuadNode::quad_1 || r == QuadNode::quad_2 ? miny : (miny + maxy) / 2;
                    int ay = r == QuadNode::quad_1 || r == QuadNode::quad_2 ? (miny + maxy) / 2 : maxy;
                    QuadNode *node = new QuadNode(data, ix, ax, iy, ay, deep - 1, r);
                    node->Parent = this;
                    Children[r] = node;
                }
                if (Children[r]->CheckInRange(index))
                {
                    return Children[r]->GetDeepest(index);
                }
            }
        }
        return this;
    }
    bool CheckInRange(int index)
    {
        if ((*data)[index][0] >= minx && (*data)[index][2] <= maxx && (*data)[index][1] >= miny && (*data)[index][3] <= maxy)
        {
            return true;
        }
        return false;
    }
    bool CheckCover(int index)
    {
        QuadNode* n = GetDeepest(index);
        QuadNode* parent = n->Parent;
        while (parent)
        {
            if (parent->CheckWithTrianglelist(index))
            {
                return true;
            }
            parent = parent->Parent;
        }

        if (n->CollisionCheck(index))
            return true;
        n->rectlist.push_back(index);
        return false;
    }
    bool CollisionCheck(int index)
    {
        return CheckWithTrianglelist(index) || CheckWithSubSpace(index);
    }
    bool CheckWithTrianglelist(int index)
    {
        RecListIter itr = rectlist.begin();
        while (itr != rectlist.end())
        {
            int id = *itr;
            if (Cover((*data)[id], (*data)[index]))
            {
                return true;
            }
            itr++;
        }
        return false;
    }

    bool CheckWithSubSpace(int index)
    {
        bool collision = false;
        for (int i = 0; i < quad_count && Children[i]; i++)
        {
            int vec[] = { minx, miny, maxx, maxy };
            vector<int> para(vec, vec + 4);
            if (Cover((*data)[index], para))
            {
                collision |= Children[i]->CollisionCheck(index);
            }
            if (collision)
            {
                return true;
            }
        }
        return false;
    }

    bool Cover(vector<int>& a, vector<int>&b)
    {
        if (min(a[0], a[2]) >= max(b[0], b[2]) || max(a[0], a[2]) <= min(b[0], b[2])
            || min(a[1], a[3]) >= max(b[1], b[3]) || max(a[1], a[3]) <= min(b[1], b[3]))
        {
            return false;
        }
        return true;
    }
};
class Solution {
public:
    int GetMax2Power(int xmax, int ymax, int& lg)
    {
        int max = xmax;
        if (ymax > max)
            max = ymax;
        if ((max & (max - 1)) == 0)
        {
            double L = log(max*1.0) / log(2.0);
            lg = (int)L + 1;
            return max;
        }
        else
        {
            double L = log(max*1.0) / log(2.0);
            lg = (int)L + 2;
            return (int)pow(2 * 1.0, lg - 1.0);
        }
    }
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        int minx, miny, maxx, maxy;
        minx = miny = INT_MAX;
        maxx = maxy = INT_MIN;
        long long int sum = 0;
        for (int i = 0; i < rectangles.size(); i++)
        {
            minx = min(minx, min(rectangles[i][0], rectangles[i][2]));
            miny = min(miny, min(rectangles[i][1], rectangles[i][3]));
            maxx = max(maxx, max(rectangles[i][0], rectangles[i][2]));
            maxy = max(maxy, max(rectangles[i][1], rectangles[i][3]));
        }
        int mx = max(abs(maxx), abs(minx));
        int my = max(abs(maxy), abs(miny));
        int range, lg;
        range = GetMax2Power(mx, my, lg);
        //四叉树
        QuadNode* root = new QuadNode(&rectangles, -range, range, -range, range, lg, 0);

        for (int i = 0; i < rectangles.size();i++)
        {
            if (root->CheckCover(i))
            {
                return false;
            }
            sum += abs((rectangles[i][0] - rectangles[i][2])*(rectangles[i][1] - rectangles[i][3]));
        }
        delete root;
        return sum == (maxx - minx)*(maxy - miny);
    }
};

以为没什么问题了，跑一下又超时了，真是恶心的一p啊。拿测试数据跑一跑发现，几乎95%的数据都在边界上，四叉树无法往下细化。写个四叉树容易吗？？？

只能硬着头皮继续想了,果然没有想到。参考了下别人的歪门邪道，感觉前面写的东西都白瞎了。有时候解决问题，还得靠技巧。

解法三：所有的矩形顶点，有且只有四个边角是只出现一次，剩下的顶点要么两次，要么四次

 

　　 long long int getHash(int x, int y)
    {
        long long int t = 2 << 16;
        return x*t + y;
    }
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        int minx, miny, maxx, maxy;
        minx = miny = INT_MAX;
        maxx = maxy = INT_MIN;
        long long int sum = 0;
        unordered_set<long long int> st;
        for (int i = 0; i < rectangles.size(); i++)
        {
            minx = min(minx, min(rectangles[i][0], rectangles[i][2]));
            miny = min(miny, min(rectangles[i][1], rectangles[i][3]));
            maxx = max(maxx, max(rectangles[i][0], rectangles[i][2]));
            maxy = max(maxy, max(rectangles[i][1], rectangles[i][3]));
            sum += abs((rectangles[i][0] - rectangles[i][2])*(rectangles[i][1] - rectangles[i][3]));
            long long int lu = getHash(rectangles[i][0], rectangles[i][3]);
            long long int ld = getHash(rectangles[i][0], rectangles[i][1]);
            long long int ru = getHash(rectangles[i][2], rectangles[i][3]);
            long long int rd = getHash(rectangles[i][2], rectangles[i][1]);
            if (st.count(lu) == 0) st.insert(lu);
            else st.erase(lu);
            if (st.count(ld) == 0) st.insert(ld);
            else st.erase(ld);
            if (st.count(ru) == 0) st.insert(ru);
            else st.erase(ru);
            if (st.count(rd) == 0) st.insert(rd);
            else st.erase(rd);
        }
        
        return sum == (maxx - minx)*(maxy - miny) && st.size() == 4 
            && st.count(getHash(minx, miny)) == 1
            && st.count(getHash(minx, maxy)) == 1
            && st.count(getHash(maxx, miny)) == 1
            && st.count(getHash(maxx, maxy)) == 1;
    }

吐血！