P2272 [ZJOI2007]最大半连通子图

Posted 2021-01-08 lltyyc

传送门

好好读题

读懂了题后就不难了

可以发现和强联通分量的定义有点像

强连通的要求：对于任意两点u,v都存在一条路径使得 u->v 并且 v->u

而半联通的要求：对于任意两点u,v都存在一条路径使得 u->v 或者 v->u

那么显然一个强联通分量肯定属于半联通子图

那先考虑缩点，看看缩点后的情况如何

 

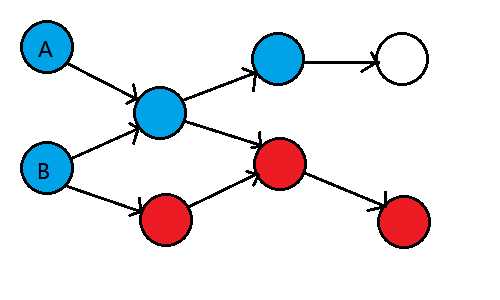
根据半联通子图的定义可以发现

在DAG上的一条路径中所有的点可以构成一个半联通子图（如红色）

并且如果有两点不在一条路径上就一定不是半联通子图（如蓝色，A不能到B且B不能到A）

所以半联通子图一定在一条路径上

那就可以在DAG上跑DP了

设 mxsz [ i ] 表示以 i 为结尾的一条路径的最大包含节点数，f [ i ] 表示以 i 为结尾时节点数为 mxsz[ i ] 时的路径方案数

那么

 

int &x=v[u][i];//u 有一条边连到 x
if(mxsz[x]==mxsz[u]+sz[x]) f[x]+=f[u];//sz[i]存联通块 i 的节点数
//注意先判断相等，因为后面一个转移会改变mxsz[x]
if(mxsz[x]<mxsz[u]+sz[x])
{
    mxsz[x]=mxsz[u]+sz[x];
    f[x]=f[u];
}

状态转移

 

要注意缩点后可能两个块之间会有很多重复边

这样会影响到DP的状态转移（同一种方案会被重复加很多次）

所以要把重复的边去除

把所有边离散化一波就好了

 

struct edge
{
    int a,b;
}e[M];//存边
inline bool cmp(const edge &x,const edge &y){ return x.a!=y.a ? x.a<y.a : x.b<y.b; }//排序函数，把边按 a,b 双关键字排序
int cnt3,du[N];//cnt存总边数，du存入度
vector <int> v[N];//直接用vector存图就好了
void build()//构造缩点后的图
{
    for(int i=1;i<=n;i++)
        for(int j=fir[i];j;j=from[j])
        {
            if(be[i]==be[to[j]]) continue;
            //这里be存每个点所在的联通块，同一个块的边不要连
            e[++cnt3].a=be[i],e[cnt3].b=be[to[j]];//把边先统一存到e里面
        }
    sort(e+1,e+cnt3+1,cmp);//离散化
    for(int i=1;i<=cnt3;i++)
        if(e[i].b!=e[i-1].b||e[i].a!=e[i-1].a) //因为排好序了，所以可以这样判断重复的边
            v[e[i].a].push_back(e[i].b),du[e[i].b]++;//如果没重复就加入DAG
}

去除重边

 

 

然后就是代码了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<‘0‘||ch>‘9‘)
    {
        if(ch==‘-‘) f=-1;
        ch=getchar();
    }
    while(ch>=‘0‘&&ch<=‘9‘)
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
const int N=2e5+7,M=2e6+7;
int n,m,mo;
int fir[N],from[M],to[M],cnt;
inline void add(int &a,int &b)
{
    from[++cnt]=fir[a];
    fir[a]=cnt; to[cnt]=b;
}

//Tarjan模板
int dfn[N],low[N],be[N],st[N],sz[N],cnt2,dfs_clock,_top;
void Tarjan(int x)
{
    dfn[x]=low[x]=++dfs_clock; st[++_top]=x;
    for(int i=fir[x];i;i=from[i])
    {
        int &v=to[i];
        if(!dfn[v]) Tarjan(v),low[x]=min(low[x],low[v]);
        else if(!be[v]) low[x]=min(low[x],dfn[v]);
    }
    if(low[x]==dfn[x])
    {
        cnt2++;
        while(st[_top]!=x)
        {
            be[st[_top--]]=cnt2;
            sz[cnt2]++;
        }
        be[st[_top--]]=cnt2;
        sz[cnt2]++;
    }
}

//构造DAG
struct edge
{
    int a,b;
}e[M];
inline bool cmp(const edge &x,const edge &y){ return x.a!=y.a ? x.a<y.a : x.b<y.b; }
int cnt3,du[N];
vector <int> v[N];
void build()
{
    for(int i=1;i<=n;i++)
        for(int j=fir[i];j;j=from[j])
        {
            if(be[i]==be[to[j]]) continue;
            e[++cnt3].a=be[i],e[cnt3].b=be[to[j]];
        }
    sort(e+1,e+cnt3+1,cmp);//把边离散化
    for(int i=1;i<=cnt3;i++)
        if(e[i].b!=e[i-1].b||e[i].a!=e[i-1].a) v[e[i].a].push_back(e[i].b),du[e[i].b]++;//去重
}

int ans,f[N],mxsz[N],mx;
queue <int> q;
void DP()
{
    for(int i=1;i<=cnt2;i++) if(!du[i]) q.push(i),f[i]=1,mxsz[i]=sz[i];//初始状态
    while(!q.empty())
    {
        int u=q.front(),len=v[u].size(); q.pop();
        mx=max(mx,mxsz[u]);
        for(int i=0;i<len;i++)
        {
            int &x=v[u][i];
            if(mxsz[x]==mxsz[u]+sz[x]) f[x]=(f[x]+f[u])%mo;
            if(mxsz[x]<mxsz[u]+sz[x])
            {
                mxsz[x]=mxsz[u]+sz[x];
                f[x]=f[u];
            }
            if(!(--du[x])) q.push(x);//更新入度
        }
    }
    for(int i=1;i<=cnt2;i++)
        if(mxsz[i]==mx) ans=(ans+f[i])%mo;//累计答案
}

int main()
{
    int a,b;
    n=read(); m=read(); mo=read();
    for(int i=1;i<=m;i++)
    {
        a=read(); b=read();
        add(a,b);
    }
    for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i);//缩点
    build();//构图
    DP();//DP
    printf("%d
%d",mx,ans);
    return 0;
}