特别翔实的adaboost分类算法讲解 转的

Posted 2021-01-08 babyfei

转https://www.cnblogs.com/litthorse/p/9332370.html

作为(曾)被认为两大最好的监督分类算法之一的adaboost元算法(另一个为前几节介绍过的SVM算法)，该算法以其简单的思想解决复杂的分类问题，可谓是一种简单而强大的算法，本节主要简单介绍adaboost元算法，并以实例看看其效果如何。

该算法简单在于adaboost算法不需要什么高深的思想，它的基础就是一个个弱小的元结构（弱分类器），比如就是给一个阈值，大于阈值的一类，小于阈值的一类，这样的最简单的结构。而它的强大在于把众多个这样的元结构（弱分类器）组合起来一起发挥功效，所谓人多力量大，就是这个道理，组合起来的最终的分类器就是一个强分类器了。相比于SVM，SVM本身是一个个体，本身也就是一个强分类器，是一个天生的天才，而adaboost元算法，把它比如下更像是后天的天才，努力的天才，是建立在广大人名群众上面的天才。

好了，言归正传，所谓元算法，就是建立在元结构基础上，也就是一个个弱分类器（广大人民群众），这个弱分类器可以任何的分类器，可以是简单决策树、简单线性logistic分类器，简单的svm等等，都可以作为它的第一层弱分类器。而一般情况下采用单层决策树分类器作为基础的分类器比较多。所谓单层决策树就是给一个或者多个阈值，将一系列数分成好几堆一样。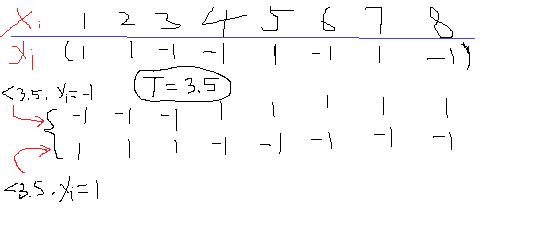 
 
比如下面的一维数据X，其对应的标签如下为y，那么如果任意给定一个阈值T=3.5，那么就可以把X分成两类了，这里就有个问题，小于T的是分成类1还是类-1呢？所以会存在两种情况吧，如上面所示，至于这个阈值好不好，小于T的是归类为1好还是-1好，那后面再说。

本节就是以这种简单的单阈值的决策树作为算法的元结构，也就是弱分类器来实现强分类器。好了再回来说刚刚的问题，首先你怎么知道阈值T=3.5，答案是不知道，那么只能一个个取了。我找到数据X的上下限，然后设置一个步长比如10步，然后就让T从最小值慢慢往上加吧。假设加到了T=3.5了，这个时候到了小于T是取1还是-1的时候了，所以又得分类讨论如果为1，如果为-1。那么我们怎么去判断阈值究竟是哪一个T好了？好了之后数据小于阈值T是是+1还是-1呢？我们看到，对于每一个阈值，然后对于该阈值下的一个取值方向（也就是小于T是+1还是-1），都会出来一个分类结果吧，有了这个结果，我把它与正确的分类结果挨个去比较看看错误率是多少，这样是不是有一个评价标准了，有了这个评价标准就可以知道在遍历所有的T的时候到底是选择那个T最好，同时是选择小于T的为-1还是+1的情况比较好。比如上面那个图，在T为3.5的时候，如果小于T取-1，那么错了5个，所以错误率为5/8。如果小于T取+1，那么正好相反错了3个，错误率3/8，所以这个时候T=3.5时小于T的取+1类比较好。上面只给了T=3.5的，那么你是不是还可以算T=4,5，等等的情况，这样遍历一圈后，找到那个最小错误率下的T以及方向是不是就知道这一组数据在这个单层决策树下的阈值以及阈值的方向了。

那这是一维数据，如果是二维数据怎么使用单层决策树呢？要是二维的，那就一维一维的来吧，比如一个二维样本点如下：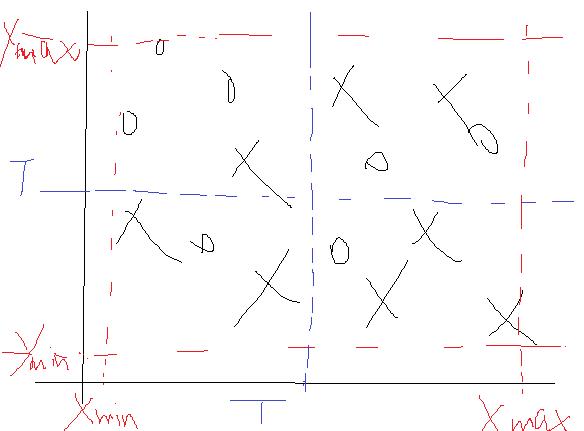 
 
那这个时候我们先找X维的数据，也就是把所有点的x坐标提出来作为一个一维样本，然后进行寻找最佳T与方向，方法同上面那样，不过这个时候找到的T还多了一个标记，就是它是在哪一维上的最小误差，比如说先找X维，那么在X维找完后，就需要记录三个值，一个是维度比如为1代表是在第一位上找的。一个是T，就是阈值，一个是T的方向，就是小于T的值是取+1还是-1，当然还有这一维下的最小错误率。完事后转战到第二维Y，在Y上同样遍历所有的T，不过这个时候遍历的时候就要和X维找完了的那个最小错误率比较，也就是说如果在Y维上还能找到一个阈值T使得划分的结果的错误率还小，那么就更新这个T。所以在遍历了所有的X维与Y维后的最优结果就需要有这么几个参数：一是最佳T来自于哪一维，二是这个T是多少，三是这个T下的方向是+1还是-1，四是对应下的错误率是多少。

那这是二维，同理可以扩展到多维吧。 
好了这样一个弱分类器（元结构）就完成了。如果单单去用这个弱分类器去分类的话显然是不准的，这也就好比是在x或者y的某一处画了一条直线，然后按照这条直线去分一样。如果碰巧数据时线性的，效果会好点，碰到非线性的，效果肯定不会好的。

说了半天，我们才把一个人的力量（弱分类器）说完，我们说adaboost元算法是众人的力量，也就是系列弱分类器的力量，那么这一系列弱分类器是怎么联系起来的呢？

上面还说漏了一点内容，就是每个样本点所占的权重问题，也就是每个样本点在最终错误率上占有的比重，反之就是对正确率上占有的比重。比如上面那个二维样本由15个样本点，那么我可以给相同的权重，同时为了保证所有的权重和为1，所以初始化权重D=[1/15,1/15,…….]等等15个1/15。那么这个权重表现在哪里呢？最后我们在算错误率的时候是不是需要寻找预测的与真实的类标签差别吗？那么这个权重可以用在这里，与这个差相乘。也就是如果标签相同，差为0，对应的权重相乘完还是0，没有用到，但是一旦不为0，那么权重就会使得这个差按权重比例放大是不是？所以说这个权重就可以用来计算那些不一样的点，并使得结果变得更好。

好了权重说完了，再来看看这一系列弱分类器是怎么联系起来的，其实联系的方式就是改变上述权重D的过程。具体怎么改变的呢？首先我们需要规定有多少个弱分类器，这需要自己设置。然后我们挨个的去找每个弱分类器的参数（这个参数就是上述的那几个输出值：属于哪一维？T是多少？T的方向？最小误差？当然这里还多出一个，这个弱分类器的D是多少？）。

既然挨个的去找每个弱分类器的参数，那么第一个弱分类器首先就假设一个D=[1/15,1/15,…….]，权重均等，有多少个样本，每个样本权重就是多少分之一。然后去找吧，最终会出来T及其参数吧。那么第一个弱分类器找完了。接下来第二个弱分类器，若果D不做任何改变，是不是第二个弱分类器出来的结果T什么的和第一个会一模一样？对，就是一样。那么这个时候关键的地方来了，第二个弱分类器会学习第一个弱分类器，假设第一个弱分类器出来的结果，错误率为?,那么

 

 

我们来分析一下，在?出来后，那么α也就定了，并且是个大于0的数吧。那么如果某个样本分对了，去看看那个公式，发现其对应的权值D变小了，而如果某个样本分错了，其对应的D会变大的。好了对于这一次的弱分类器，一旦完成后我们就去更新它的D，并且把这个D传递到下一次的弱分类器构建中。我们再想想，比如说上次样本1在上一个弱分类器中分错了，那么它的D就会增加吧，把么它传到这一次的弱分类时，在计算它产生的误差的时候，就会因为D的增加而把使得误差变大吧，所以这一次寻找的结果就不会是上一次寻找到T了，因为这个时候D会把第一个样本点产生的误差值拉大的对不对。那么这个时候就会寻找到一个新的T及其相关参数了。用一个图形象表示一下：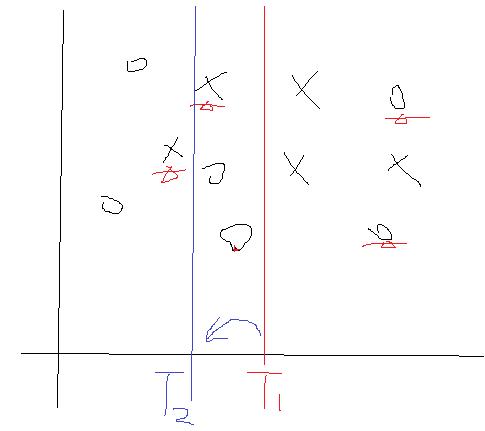 
 
划分错误的点会在下一次的划分中被一定程度的矫正过来。

这样第一次弱分类器就将更新后的D传递到第二个弱分类器的构建当中，第三个又学习第二个的弱分类器，把在第二个弱分类器中分错的点给稍微矫正过来，这样一直往下传递，弱分类器之间传递的唯一参数就是每个样本的权值D。这个过程就如下所示：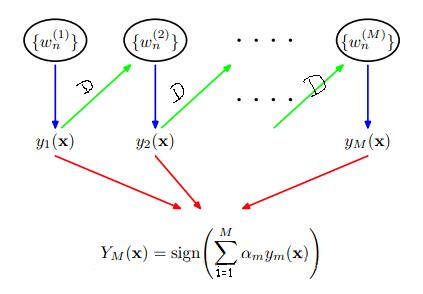 
 
那么这样就可以把所有的弱分类都找出来了吧，每个弱分类器出来的结果参数（包括阈值T，T取值方向，取阈值T所属于的原始数据维度，最小错误率–以及由错误率可以计算的α（上述公式有））是不是都可以计算出来。那么在所有这些参数计算完了之后，怎么区划分原始训练样本以及来了的预测样本的分类情况呢？就是上述那个公式了。每个弱分类器的α可以计算出来的，那y是什么呢？是预测的类别，有了一个样本，我们可以根据T属于那个维度就可以找到这个样本对应维度下的值了，然后看看这个值与阈值T的关系吧，看完关系后再看看是属于+1还是-1，这就是T的方向了吧，根据这些确定这个样本是属于+1还是-1类，这就是y。最后把所有弱分类器的所有这样的结果按照公式求和，把这个和取符号就是我们最终这个样本所属于的类了。

至此，完整的给予简单单层决策树的adaboost算法就到此结束了，那么用数学符号在规整一下整个过程如下： 

下面在matlab下实战上述过程。首先还是样本集，依然用曾经用过的非线性样本集： 

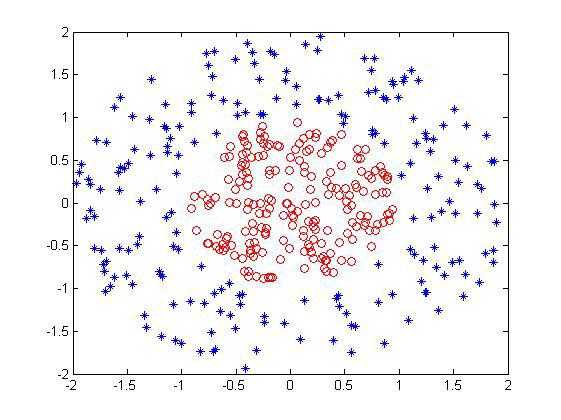
首先我们需要一个寻找一次弱分类器参数的子函数：

function [Dim,Dir,T,best_label,minError] = buildSimpleStump(data,label,D)
% 设置一个步长
numSteps = 50;
% m个样本,每个n维
[m,n] = size(data);
thresh = 0;
minError = inf;
for i = 1:n
    min_dataI = min(data(:,i));
    max_dataI = max(data(:,i));
    step_add = (max_dataI - min_dataI)/numSteps;
    for j = 1:numSteps
        threshVal = min_dataI + j*step_add; %
        index = find(data(:,i) <= threshVal);
        %-----小于阈值的取值为-1类--------------------
        label_temp = ones(m,1);
        label_temp(index) = -1;
        index1 = find(label_temp == label);
        errArr = ones(m,1);
        errArr(index1) = 0;
        %小于阈值的误差
        weightError = D‘*errArr;
        if weightError < minError
            bestLabel = label_temp;
            minError = weightError;
            %小于阈值的点取-1标签
            direction = -1;
            Dim = i; %记录属于的维度
            thresh = threshVal;
        end      
        %-----------小于阈值的取值为+1类---------
        label_temp = -1*ones(m,1);
        label_temp(index) = 1;
        index1 = find(label_temp == label);
        errArr = ones(m,1);
        errArr(index1) = 0;
        %大于阈值的误差
        weightError = D‘*errArr;
        if weightError < minError
            bestLabel = label_temp;
            minError = weightError;
            %小于阈值的点取+1标签
            direction = 1;
            Dim = i; %记录属于的维度
            thresh = threshVal;
        end  
    end
end
Dir = direction;
T = thresh;
best_label = bestLabel;

其次需要建立所有的弱分类器：

function [dim,direction,thresh,alpha] = adaBoostTrainDs(data,label,iter)
[m,~] = size(data);
% 初始化权值D
D = ones(m,1)/m;
alpha = zeros(iter,1);
% 记录T方向
direction = zeros(iter,1);
% 记录T属于哪一个维度
dim = zeros(iter,1);
% 初始化阈值T
thresh = zeros(iter,1);
for i = 1:iter
    [dim(i),direction(i),thresh(i),best_label,error] = ...
        buildSimpleStump(data,label,D);
    %计算alpha
    alpha(i) = 0.5*log((1-error)/max(error,1e-15));
    %更新权值D
    D = D.*(exp(-1*alpha(i)*(label.*best_label)));
    D = D/sum(D);
end

那么主函数以及显示结果如下：

clc
clear
close all
%% 加载数据
% * 最终data格式：m*n，m样本数，n维度
% * label:m*1  标签为-1与1这两类
clc
clear
close all
data = load(‘data_test1.mat‘);
%选择训练样本个数
num_train = 200;
%构造随机选择序列
choose = randperm(length(data));
train_data = data(choose(1:num_train),:);
label_train = train_data(:,end);
train_data = train_data(:,1:end-1);
test_data = data(choose(num_train+1:end),:);
label_test = test_data(:,end);
test_data = test_data(:,1:end-1);
predict = zeros(length(test_data),1);
%% -------训练集训练所有的弱分类器
iter = 50; %规定弱分类器的个数
[dim,direction,thresh,alpha] = adaBoostTrainDs(train_data,label_train,iter);
%% -------预测测试集的样本分类
for i = 1:length(test_data)
    data_temp = test_data(i,:);
    h = zeros(iter,1);
    for j = 1:iter
        if direction(j) == -1
            if data_temp(dim(j)) <= thresh(j)
                h(j) = -1;
            else
                h(j) = 1;
            end
        elseif direction(j) == 1
            if data_temp(dim(j)) <= thresh(j)
                h(j) = 1;
            else
                h(j) = -1;
            end
        end
    end
    predict(i) = sign(alpha‘*h);
end
%% 显示结果
figure;
index1 = find(predict==1);
data1 = (test_data(index1,:))‘;
plot(data1(1,:),data1(2,:),‘or‘);
hold on
index2 = find(predict==-1);
data2 = (test_data(index2,:))‘;
plot(data2(1,:),data2(2,:),‘*‘);
hold on
indexw = find(predict~=(label_test));
dataw = (test_data(indexw,:))‘;
plot(dataw(1,:),dataw(2,:),‘+g‘,‘LineWidth‘,3);
accuracy = length(find(predict==label_test))/length(test_data);
title([‘predict the testing data and the accuracy is :‘,num2str(accuracy)]);

某次的结果如下：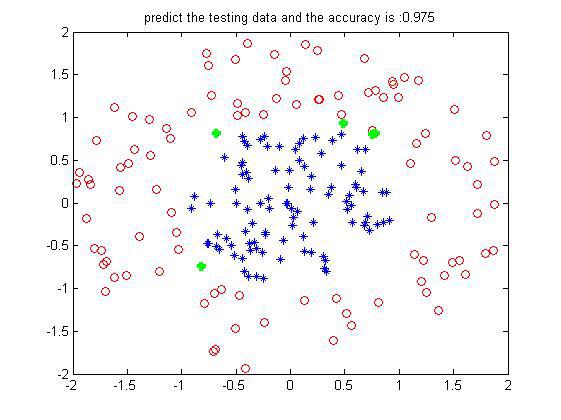 
 
这是200个训练样本下200个测试样本的预测结果（数据边界没有交叉的），可以看到设置的弱分类器iter为50个，每一维度步长为50，正确率还挺好。当然是不是弱分类器数目越多越好了？不一定，多了的话可能会过拟合，且到达一定程度正确率不会有太大的提升了。其实一个样本从第一个弱分类器到最后一个弱分类器，就相对于每经过一次在上面集合切一刀一样，最后越来越小越来越小，就属于哪一个类了。借用网上别人的一个图形象表示就如下：

每一个弱分类器切一次：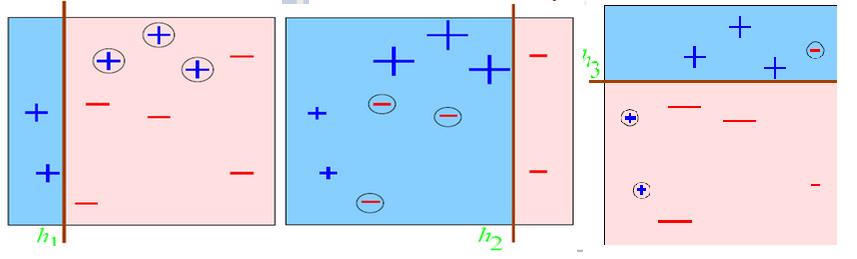 

组合起来的分类面就是：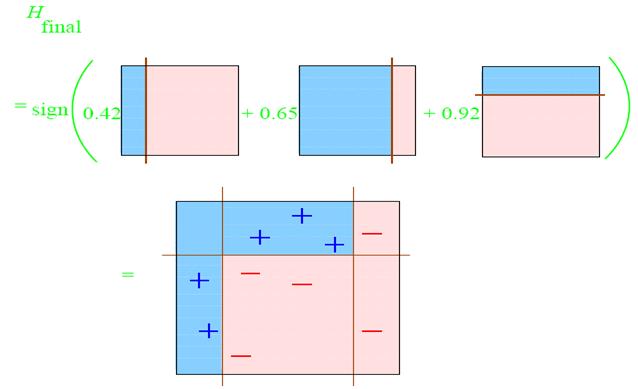 

这就是团结的力量。

----------------------------------------------------这里是分割线-------------------------------------------------------------------------------------

上面是二分类情况，接下来是多分类：

既然是多分类样本，首先对样本需要理解，所谓多分类就是样本集中不止2类样本，至少3类才称得上是多分类。比如下面一个二维非线性的多类样本集（这也是后面我们实验的样本集）：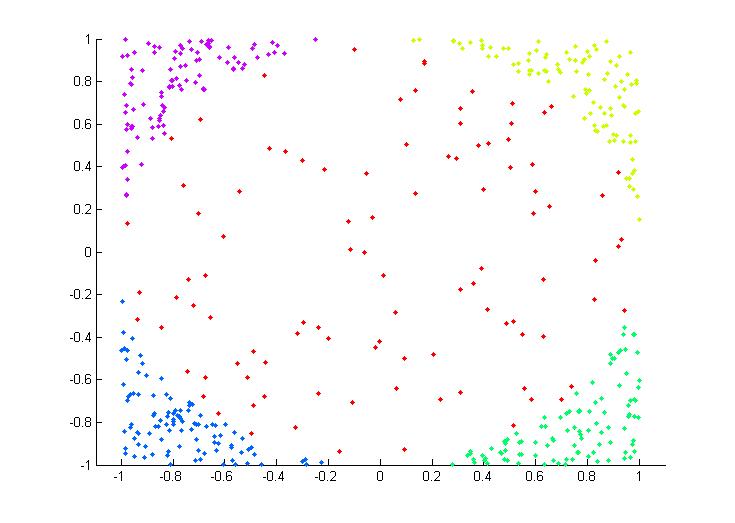 
 
每种颜色代表一类，可以看到共有5类，同时也可以看到是一个非线性的吧，这里可以就把五类分别设置为1~5类类标签。

好了，曾经在单个算法介绍的时候，里面的实验都是二分类的（也就是只有上述5类样本中的两类），二分类的方式很简单，不是你就是我的这种模式，那么从二分类到多分类该怎么转换呢？假如一个样本不是我，那也可能不是你呀，可能是他它她对吧，这个时候该如何呢？

现在一般的方式都是将多分类问题转化为二分类问题，因为前面许多算法在原理推导上都是假设样本是二分类的，像SVM，整个推导过程以至结论都是相对二分类的，根本没有考虑多分类，依次你想将SVM直接应用于多分类是不可能的，除非你在从原理上去考虑多分类的情况，然后得到一个一般的公式，最后在用程序实现这样才可以。

那么多分类问题怎么转化为二分类问题？很简单，一个简单的思想就是分主次，采取投票机制。转化的方式有两种，因为分类问题最终需要训练产生一个分类器，产生这个分类器靠的是训练样本，前面的二分类问题实际上就是产生了一个分类器，而多分类问题根据训练集产生的可不止是一个分类器，而是多个分类器。

那第一种方式就是将训练样本集中的某一类当成一类，其他的所有类当成另外一类，像上面的5类，我把最中间的一类当成是第一类，并重新赋予类标签为1，而把四周的四类都认为是第二类，并重新赋予类标签维-1，好了现在的问题是不是就是二分类问题了？是的。那二分类好办，用之前的任何一个算法处理即可。好了，这是把最中间的当成一类的情况下建立的一个分类器。同理，我们是不是也可以把四周任何一类自成一类，而把其他的统称为一类呀？当然可以，这样依次类推，我们共建立了几个分类器？像上面5类就建立了5个分类器吧，好了到了这我们该怎么划分测试集的样本属于哪一类了？注意测试集是假设不知道类标签的，那么来了一个测试样本，我把它依次输入到上述建立的5个分类器中，看看最终它属于哪一类的多，那它就属于哪一类了吧。比如假设一个测试样本本来是属于中间的（假设为第5类吧），那么先输入第五类自成一类的情况，这个时候发现它属于第五类，记录一下5，然后再输入左上角（假设为1类）自成一类的情况，那么发现这个样本时不属于1类的，而是属于2,3,4,5这几类合并在一起的一类中，那么它属于2,3,4,5中的谁呢？都有可能吧，那么我都记一下，此时记一下2,3,4,5。好了再到有上角，此时又可以记一下这个样本输入1,3,4,5.依次类推，最后把这5个分类器都走一遍，就记了好多1~5的标签吧，然后去统计他们的数量，比如这里统计1类，发现出现了3次，2,3,4都出现了3次，就5出现了5次，那么我们就有理由认为这个样本属于第五类，那么现在想想是不是就把多类问题解决了呢？而这个过程参考这位大神博客中的一张图表示就如下：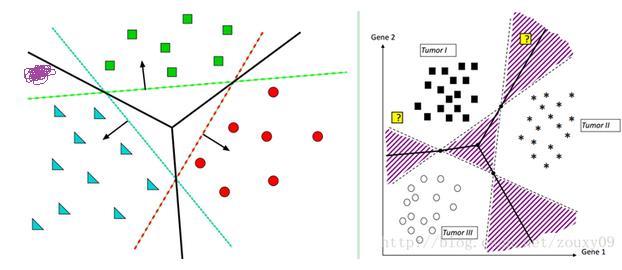 
 
可以看到，其实黑实线本类是我们想要的理想分类面，而按照这种方式建立的分类面是带阴影部分的那个分类面，那阴影部分里面表示什么呢？我们想想，假设一个样本落在了阴影里面，比如我画的那个紫色的点，按照上面计算，发现它属于三角形一类的2次，属于正方形一类的2次，属于圆形一类的1次，那这个时候你怎么办？没招，只能在最大的两次中挑一个，运气好的认为属于三角形，挑对了，运气不好的挑了个正方形，分错了。所以阴影部分是属于模棱两可的情况，这个时候只能挑其中一个了。

这是第一种方式，那还有第二种分类方式，思想类似，也是转化为二分类问题，不过实现上不同。前面我们是挑一类自成一类，剩下的所有自成一类，而这里，也是从中挑一类自成一类，然剩下的并不是自成一类，而是在挑一类自成一类，也就是说从训练样本中挑其中的两类来产生一个分类器。像上述的5类，我先把1,2,类的训练样本挑出来，训练一个属于1,2,类的分类器，然后把1,3,挑出来训练一个分类器，再1,4再1,5再2,3,等等（注意2,1与1,2一样的，所以省去了），那这样5类样本需要建立多少个分类器呢？n*(n-1)/2吧，这里就是5*4/2=10个分类器，可以看到比上面的5个分类器多了5个。而且n越大，多的就越多。好了建立完分类器，剩下的问题同样采取投票机制，来一个样本，带到1,2建立的发现属于1，属于1类的累加器加一下，带到1,3建立的发现也属于1，在加一下，等等等等。最后看看5个类的累加器哪个最大就属于哪一类。那么一个问题来了，会不会出现像上面那种情况，有两个或者更多个累加器的值是一样的呢？答案是有的，但是这种情况下，出现一样的概率可比上述情况的概率小多了（比较是10个分类器来的结果，怎么也得比你5个的要好吧），同样一个示意图如下：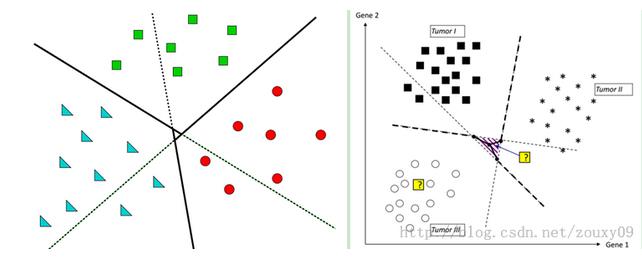 
 
可以看到重叠部分就是中间那么一小块，相比上面那种方式小了不少吧。 
那么细比较这两种方式，其实各有优缺点。第一种方式由于建立的分类器少（n越大越明显吧，两者相差(n*(n-1)/2 - n）个分类器）。也就是在运算的时候速度更快，而第二种方式虽然速度慢，但是精度高呀，而且现在计算机的速度也够快了，可以弥补第二种方式的缺点，所以个人更倾向于第二种方式了。 

在基于上述的两个子函数下，我们在编写两个函数，一个是adaboost的训练函数，一个是adaboost的预测函数，函数如下： 
训练函数：

 

function model = adaboost_train(label,data,iter)
[model.dim,model.direction,model.thresh,model.alpha] = ...
    adaBoostTrainDs(data,label,iter);
model.iter = iter;

预测函数：

function predict = adaboost_predict(data,model)
h = zeros(model.iter,1);
for j = 1:model.iter
    if model.direction(j) == -1
        if data(model.dim(j)) <= model.thresh(j)
            h(j) = -1;
        else
            h(j) = 1;
        end
    elseif model.direction(j) == 1
        if data(model.dim(j)) <= model.thresh(j)
            h(j) = 1;
        else
            h(j) = -1;
        end
    end
end
predict = sign(model.alpha‘*h);

有了这两个函数我们就可以进行实验了，这里我们只以第二种方式的多分类为例，函数同上面的svm类似，只不过把那里的训练模型函数与预测函数改到我们这里的这种，主函数如下：

%%  
% * adaboost
% * 多类非线性分类
% 
%% 
clc
clear
close all
%% Load data
% * 数据预处理
data = load(‘data_test.mat‘);%选择训练样本个数
num_train = 200;
%构造随机选择序列
choose = randperm(length(data));
train_data = data(choose(1:num_train),:);
gscatter(train_data(:,1),train_data(:,2),train_data(:,3));
label_train = train_data(:,end);
test_data = data(choose(num_train+1:end),:);
label_test = test_data(:,end);
%% adaboost的构建与训练
num = 0;
iter = 30;%规定弱分类器的个数
for i = 1:5-1 %5类
    for j = i+1:5 
        num = num + 1;
        %重新归类
        index1 = find(label_train == i);
        index2 = find(label_train == j);
        label_temp = zeros((length(index1)+length(index2)),1);
        %svm需要将分类标签设置为1与-1
        label_temp(1:length(index1)) = 1;
        label_temp(length(index1)+1:length(index1)+length(index2)) = -1;
        train_temp = [train_data(index1,:);train_data(index2,:)];
        % 训练模型
        model{num} = adaboost_train(label_temp,train_temp,iter);
    end
end
% 用模型来预测测试集的分类
predict = zeros(length(test_data),1);
for i = 1:length(test_data)
    data_test = test_data(i,:);
    num = 0;
    addnum = zeros(1,5);
    for j = 1:5-1
        for k = j+1:5
            num = num + 1;
            temp = adaboost_predict(data_test,model{num});
            if temp > 0
                addnum(j) = addnum(j) + 1;
            else
                addnum(k) = addnum(k) + 1;
            end
        end
    end
    [~,predict(i)] = max(addnum);
end
%% show the result--testing
figure;
gscatter(test_data(:,1),test_data(:,2),predict);
accuracy = length(find(predict==label_test))/length(test_data);
title([‘predict the testing data and the accuracy is :‘,num2str(accuracy)]);

这还是在200个训练样本下300个测试样本的一个结果如下：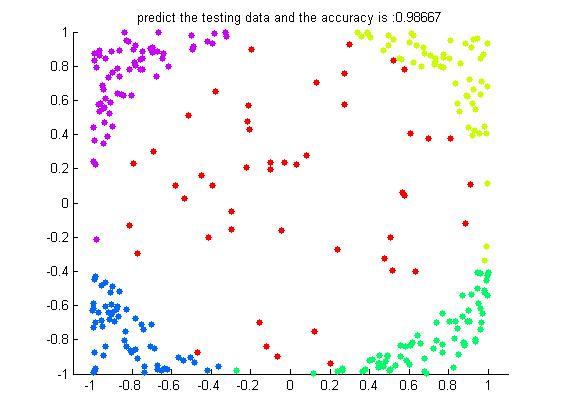 
 
可以看到在iter=30个弱分类器下的结果已经是高的惊人了。

附上二分类数据集产生代码：

%% % * Logistic方法用于回归分析与分类设计 % * 多类问题的分类 % %% 产生非线性数据 2类 200个 clc clear close all data1 = rand(1,1000)*4 + 1; data2 = rand(1,1000)*4 + 1; circle_inx = data1 - 3; circle_iny = data2 - 3; r_in = circle_inx.^2 + circle_iny.^2; index_in = find(r_in<0.8); data_in = [data1(index_in(1:100));data2(index_in(1:100));-1*ones(1,100)]; data1 = rand(1,1000)*4 + 1; data2 = rand(1,1000)*4 + 1; circle_inx = data1 - 3; circle_iny = data2 - 3; r_in = circle_inx.^2 + circle_iny.^2; index_out = find((r_in>1.2)&(r_in<4)); data_out = [data1(index_out(1:100));data2(index_out(1:100));ones(1,100)]; plot(data_in(1,:),data_in(2,:),‘or‘); hold on; plot(data_out(1,:),data_out(2,:),‘*‘); data = [data_in,data_out]; save data_test1.mat data