算法学习——递推之超级素数
Posted kexing
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法学习——递推之超级素数相关的知识,希望对你有一定的参考价值。
算法描述
超级素数定义:
- m位超级素数本身是素数
- 最高位开始,去掉一位为m-1位的素数……
例: 103不是超级素数,去掉最高位的1之后为3,不是有个2位素数,137是一个三位超级素数,去掉最高位1之后为37,37是一个二位素数,去掉3之后为7,7也是一个素数
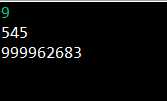
要求: 输入整数m(1 < m<=10),统计m位超级素数的个数,并输出其中最大的m位超级素数
算法思路
设置一个判断素数的方法
1位素数只有3个,3,5,7,我们可以推测,2位超级素数的个位数只能是3,5,7,没有其他的选择了,同理,3位超级素数的十位和个位数只能是二位的超级素数组成,由此我们就可以得到一个递推关系
算法实现
Scanner scanner = new Scanner(System.in);
int m = scanner.nextInt();
scanner.close();
int a[] = new int[10000];
int b[] = new int[10000];
int count =0;//统计超级素数的个数
int g = 3;//记录每一个位的超级素数,当前记录的是个位的3个超级素数,3,5,7 之后每一位都会重新赋值
a[0] = 3;
a[1] = 5;
a[2]=7;
//i表示十位,所以这里i要小于m
for(int i=1;i<m;i++){
int t =0;
int e = (int) Math.pow(10, i);//表示十位,百位…… 每一个位的阶乘
//j*e 10,20…… 100,200……
for(int j=1;j<=9;j++){
//遍历a数组的全部素数
for(int k=0;k<g;k++){
if(panduan(e*j+a[k])){
b[t] = e * j +a[k];
t++;//统计在当前位的超级素数的个数,之后再赋值给g
if(i==m-1){
count++;//统计
}
}
}
}
g=t;
//将b数组中的数据转移动a数组中,便于之后的递推
for(int z=0;z<g;z++){
a[z] = b[z];
}
}
System.out.println(count);
//冒泡排序,输出最大值
for(int i=0;i<a.length-1;i++){
for(int j=i+1;j<a.length;j++){
if(a[i]<a[j]){
int t = a[i];
a[i]=a[j];
a[j]=t;
}
}
}
System.out.println(a[0]);
}
/**
*
* @param a
* @return 通过试商法判断a是否为素数
*/
public static boolean panduan(int a){
int s = (int)Math.sqrt(a);
for(int i=2;i<=s;i++){
if(a%i==0){
return false;
}
}
return true;
}结果
以上是关于算法学习——递推之超级素数的主要内容,如果未能解决你的问题,请参考以下文章