猴子课堂：最大流与最小割

Posted 2021-01-08 zhangjianjunab

 注：本人只是一个萌新，有一些地方的用语会不太专业（大佬：是十分不专业），我不会用什么技术用语，这些文章对那些跟我一样的萌新会比较适用！

 

最大流：

      原题地址

　　最大流我讲的是我自己对dinic算法的一些思想，希望对你会有用！

　　我记网络流靠三个关键字：

      1.找最短路径

　　将流量流向终点，且损害最少的边，这是找路径的一个关键，那么，便可以把分出最少的层面，以便后面的查找！

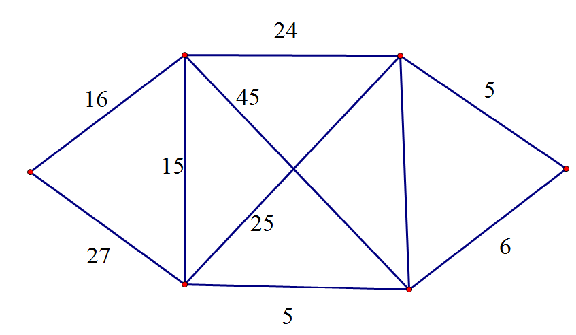
如图：

?

分层

?

分层可以用宽搜（宽搜可以保证层数最少），用h数组储存层，具体如下代码：

int  list[21000],head,tail,h[21000];
bool  bt_()
{
	memset(h,0,sizeof(h));h[st]=1;/*初始化*/
	list[1]=st;head=1;tail=2;
	while(head!=tail)
	{
		int  x=list[head];
		for(int  k=last[x];k;k=a[k].next)/*搜索相邻边*/
		{
			int  y=a[k].y;
			if(a[k].c>0  &&  h[y]==0)/*这条边的值若为0，则不存在，反之，存在，只搜存在的边和为更新的点*/
			{
				h[y]=h[x]+1;
				list[tail++]=y;
			}
		}
		head++;
	}
	if(h[ed]==0)/*若不能到达终点，也就没有流量可以到达*/return  false;
	/*反之，可以*/return  true;
}

　　

那么，分层后有什么用呢？

答案就是！每个点只能流向比他大一层的点！这样既确定的边的最少损害，又确定的一些固定路径！

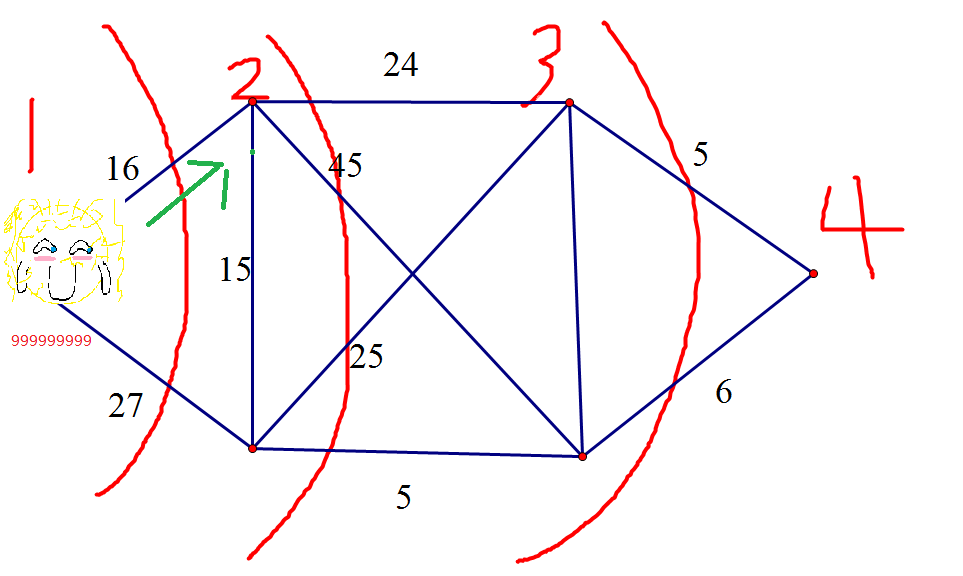
那么，到找流量了，一开始，从初始点出发有无限流量，搜索每条边，如图（滑稽为所在点，红字体为流量！）

?

搜索第二层的最上面那个点，刚好层数只比自己大一，边的剩余流量为16，自身还剩下999999999的流量可以用，于是，递归到第二层的最上面那个点，并赋予他流量16！

 

进入第二层的最上面那个点，找到了第二层最下面那个点，同层，无法进入，搜索第三层两个点，进入上面的点，将身上唯独的16赋予它，让他搜。

 

进入第二层的最上面那个点，找到了第二层最下面那个点，同层，无法进入，搜索第三层两个点，进入上面的点，将身上唯独的16赋予它，让他搜。

 

 进入第三层上面那个点，一直搜索到第四层的终点，赋予流量5，进入终点。

 

搜索终点，发现为终点，返回自己身上现有流量。

 

 回到第三层上面那个点，将总点返回的流量记录为t，表示从这条边走绝对可以到达的流量，并将这条边的值减t，将反向边的权值加t，再将t加到s（s代表已用流量），删除t，由此第三个点的现有可用流量从16变成11，继续搜索，搜索完了之后，将s返回，若s为0，顺便将这个点的层数标为0，代表在这种分层图中，这个点不能发挥他的神威，便在这个分层图内不在搜索他了（为什么说本次呢？因为要分多次并搜索多次才可以将所有的边全部巧妙的利用上）。

反向边（悔棋）处理讲在下次（十分重要）！

先给出搜索操作！

inline  int  mymin(int  x,int  y){return  x<y?x:y;}
int  find(int  x,int  f)
{
	if(x==ed)return  f;/*终点返回*/
	int  s=0/*已用流量*/,t=0;
	for(int  k=last[x];k;k=a[k].next)
	{
		int  y=a[k].y;
		if(a[k].c>0/*判断可不可用*/  &&  s<f/*已用流量不能多于可用流量*/  &&  h[y]==h[x]+1/*分层图的妙用*/)
		{
			s+=t=find(y,mymin(a[k].c,f-s));/*搜索点，赋予他自身能给予他的流量（不能超过边的值和剩余可用流量），并记录*/
			a[k].c-=t;/*将边的值减去t，代表这条边已经流过t个量*/a[a[k].other].c+=t;/*反向边流量操作，下次再讲！*/
		}
	}
	if(s==0)h[x]=0;
	return  s;
}

　　

找答案！

int  ans=0;
while(bt_()==true)/*多次作图，直到无法流到终点*/
{
	ans+=find(st,999999999);
} 

　　

 进入第三层上面那个点，一直搜索到第四层的终点，赋予流量5，进入终点。

还剩下一个反向边，其实，一开始，所有边都要多建一条双向边（至少我是这样），反向边的流量为0！

反向边是网络流里面一个十分重要的思想

还记得这段代码吗？

inline  int  mymin(int  x,int  y){return  x<y?x:y;}
int  find(int  x,int  f)
{
	if(x==ed)return  f;/*终点返回*/
	int  s=0/*已用流量*/,t=0;
	for(int  k=last[x];k;k=a[k].next)
	{
		int  y=a[k].y;
		if(a[k].c>0/*判断可不可用*/  &&  s<f/*已用流量不能多于可用流量*/  &&  h[y]==h[x]+1/*分层图的妙用*/)
		{
			s+=t=find(y,mymin(a[k].c,f-s));/*搜索点，赋予他自身能给予他的流量（不能超过边的值和剩余可用流量），并记录*/
			a[k].c-=t;/*将边的值减去t，代表这条边已经流过t个量*/a[a[k].other].c+=t;/*反向边流量操作，下次再讲！*/
		}
	}
	if(s==0)h[x]=0;
	return  s;
}

　　

反向边加t，简单来说就是给予反悔的机会！

例如：

?

为了解决这个小人的苦恼，我们建立一条反向边。小人就可以从反向边走到原本那个笨笨的人应该走的位置，并进行搜索，与其说是小人跑到那里，不如说是他把笨笨的人拉回来，让他将一些流量取回去，到那个点再次进行搜索，不过，不能走与以前一样的路径（否则叫他回来有什么用，不悔改有什么用？）。

虽然有时叫他回来可能他也没法再流到其他路径，这是，他会返回0，如果这样，和蔼的小人还是会理解他的，顶多不走就行了，因此反向边不会出现错误。

本蒟蒻的建边：

void  ins(int  x,int  y,int  c)
{
	len++;
	a[len].x=x;a[len].y=y;a[len].c=c;

	a[len].next=last[x];last[x]=len;
	len++;/*反向边*/
	a[len].x=y;a[len].y=x;a[len].c=0;

	a[len].next=last[y];last[y]=len;
	a[len].other=len-1;/*建立联系*/
	a[len-1].other=len;
}

　　

但是，Dinic不是最快的，比如：ISAP，预流推进算法等，也都是十分快的。（ISAP的博客我已经在我的博客置顶了）

不过Dinic比较简单，也十分简洁，在时间短的情况下我也更愿意敲Dinic。

好了,接下来处理最小割！

我并没有用算式证明，而是用了一种神奇的方法证明（科学家看了想骂人！）：

首先，网络流的核心是从起点通过多条路径到终点，那么，我们可以想出，这每一条合格（可以从起点流向终点）的路径，一定会有其中一条或多条边爆流了，那么，代表这条边是这条路径的核心，取掉这条边，这条边的完整流量就会减去他的流量，我们称这些边为贡献边。

 

那么，在最小割所求的最小容量中所割掉的边的集合中，一定全部是贡献边；想不明白的同学可以躲到门后想几分钟，记得带上草稿纸和笔！（大佬：这不是我幼儿园就会的吗？）（我：滚！）

为什么呢（同学：我想好一会才想明白你告诉我有解释！）？由于这些贡献边是这些路径的重要部分，因此，取掉这些边，也就会使起点无法流向终点，也就无法到达终点，且由于这些边都是满的，不会有浪费！

注意：有时候，一条路径有多条贡献边，甚至会出现两条路径共用一条贡献边，这时会有多种组合（所以，你不能说一条路径上的两条贡献边都属于这个集合，只能用另外的方法判断！）！

由于，我们知道，这个最小割集合里的边，容量代表了整个图的流量，且他们都是爆流的！所以从起点到终点的所有流量绝对会流到他们，而他们自己的流量也绝对可以流向终点（具体看前面，一条边只会减去经过他的有效流量！），所以，最小割与最大流是一样的（（想打人的）大佬：说话怎么这么不专业！）！

那么，怎么求这些边呢（编号按字典序排并且要最少的边）

由于这些贡献边控制了流量，所以，我们把他删除掉，再流一遍，会得到一个新的ans（ans可能是0），ans+这条边的权值=不删这条边的最大流，依靠这条等式，就可以去判断了，别忘了排序哟！

（注，其实如果只求割最少的边，还有另外一种方法，就是把每个容量乘以一个很大的数加1，流量=假流量/很大的数，割的边数=假流量%很大的数）

代码：

	int  ans=0;/*原本的答案*/
	while(bt_()==true)
	{
		ans+=find(st,999999999);
	}
	sort(zjj/*储存边的结构体数组*/+1,zjj+m+1,cmp);
	printf("%d ",ans);
	memset(kk,true,sizeof(kk));
	for(int  i=1;i<=m;i++)/*其实还可以加个优化，判断他是不是爆流的再进入，懒得打*/
	{
		memset(a/*用来网络流的边*/,0,sizeof(a));
		memset(last,0,sizeof(last));
		len=0;
		for(int  j=1;j<=m;j++)
		{
			if(kk[zjj[j].d]==true  &&  i!=j)ins(zjj[j].x,zjj[j].y,zjj[j].c,zjj[j].d);/*将没被删除的点*/
		}
		int  oj=0;
		while(bt_()==true)oj+=find(st,999999999);/*网络流*/
		if(oj+zjj[i].c==ans)/*判断*/
		{
			ans-=zjj[i].c;
			kk[zjj[i].d]=false;
			b[++tk]=zjj[i].d;/*记录！*/
		}
	}

　　

另外，有的最小割不是单纯的割边，而是割点，这时，可以讲一个点拆成两个点，两个点之间存在一条容量为1的单向边，进入的边连向一个点，出去的边连另一个点，便把割点化成割边（起点与终点不用分）！

如图（讲i拆开了！）：

?

然后，就尽情最小割吧！

喜欢点个赞呗

 

注：上面的图片侵权抱歉！