数据特征分析：5.相关性分析

Posted 2021-01-06 shengyang17

 相关性分析

三点图矩阵初判多变量间关系，两两数据之间的，比如说4个数据ABCD，就有12个比较，第一个参数和第二个参数，第一个参数和第三个参数，.......这个图就是正态分布的接个参数，就没有任何的相关性

 

 相关性分析  

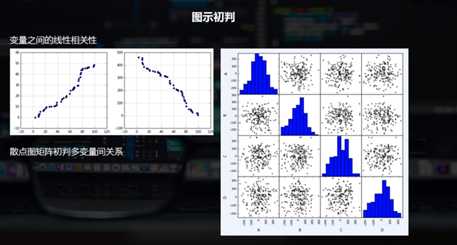
 分析连续变量之间的线性相关程度的强弱

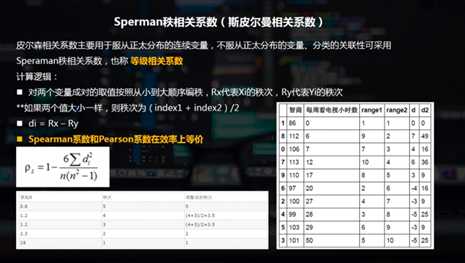
 图示初判 / Pearson相关系数（皮尔逊相关系数） / Sperman秩相关系数（斯皮尔曼相关系数）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
% matplotlib inline

# 图示初判
# （1）变量之间的线性相关性

data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False)
# 创建三个数据：data1为0-100的随机数并从小到大排列，data2为0-50的随机数并从小到大排列，data3为0-500的随机数并从大到小排列，

fig = plt.figure(figsize = (10,4))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1, data2)
plt.grid()
# 正线性相关

ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1, data3)
plt.grid()
# 负线性相关

# 图示初判
# （2）散点图矩阵初判多变量间关系

data = pd.DataFrame(np.random.randn(200,4)*100, columns = [‘A‘,‘B‘,‘C‘,‘D‘])
pd.scatter_matrix(data,figsize=(8,8),
                  c = ‘k‘,
                 marker = ‘+‘,
                 diagonal=‘hist‘,
                 alpha = 0.8,
                 range_padding=0.1)
data.head()

 

 

 

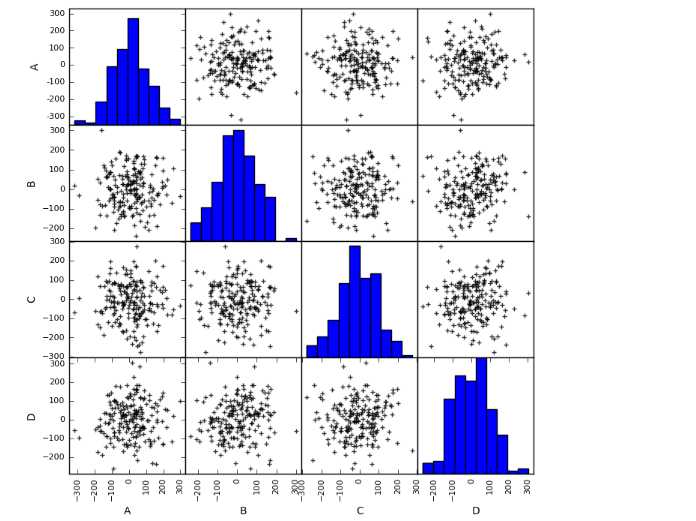
建立在正态分布之上的

分子是第一个变量X - 它的均值，第二个变量Y - 它的均值的求和，分母是两个平方根的积

 

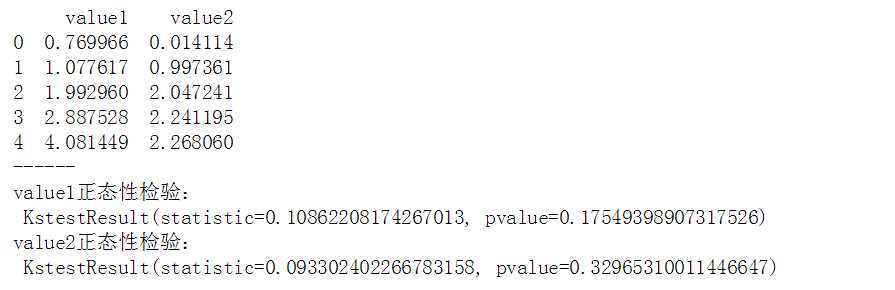
# Pearson相关系数

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({‘value1‘:data1.values,
                     ‘value2‘:data2.values})
print(data.head())
print(‘------‘)
# 创建样本数据

u1,u2 = data[‘value1‘].mean(),data[‘value2‘].mean()  # 计算均值
std1,std2 = data[‘value1‘].std(),data[‘value2‘].std()  # 计算标准差
print(‘value1正态性检验：
‘,stats.kstest(data[‘value1‘], ‘norm‘, (u1, std1)))
print(‘value2正态性检验：
‘,stats.kstest(data[‘value2‘], ‘norm‘, (u2, std2)))
print(‘------‘)
# 正态性检验 → pvalue >0.05

data[‘(x-u1)*(y-u2)‘] = (data[‘value1‘] - u1) * (data[‘value2‘] - u2)
data[‘(x-u1)**2‘] = (data[‘value1‘] - u1)**2
data[‘(y-u2)**2‘] = (data[‘value2‘] - u2)**2
print(data.head())
print(‘------‘)
# 制作Pearson相关系数求值表

r = data[‘(x-u1)*(y-u2)‘].sum() / (np.sqrt(data[‘(x-u1)**2‘].sum() * data[‘(y-u2)**2‘].sum()))
print(‘Pearson相关系数为：%.4f‘ % r)
# 求出r
# |r| > 0.8 → 高度线性相关

# Pearson相关系数 - 算法

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({‘value1‘:data1.values,
                     ‘value2‘:data2.values})
print(data.head())
print(‘------‘)
# 创建样本数据

data.corr()
# pandas相关性方法：data.corr(method=‘pearson‘, min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson

 

 

 

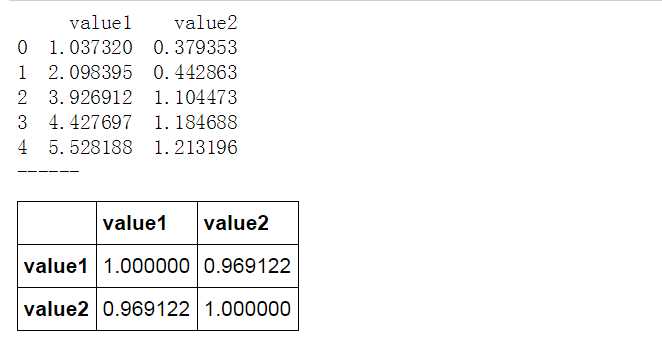
Pearson相关系数 - 算法 

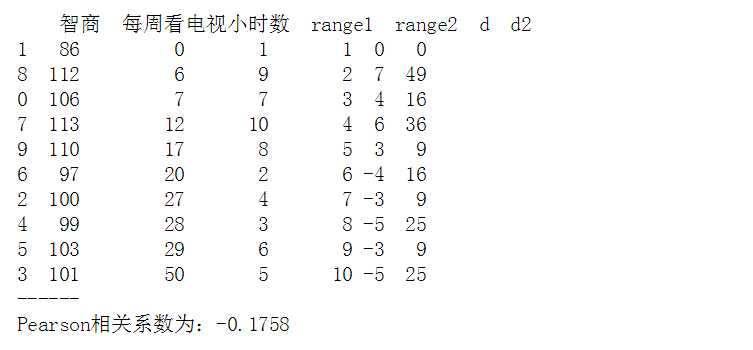
# Sperman秩相关系数

data = pd.DataFrame({‘智商‘:[106,86,100,101,99,103,97,113,112,110],
                    ‘每周看电视小时数‘:[7,0,27,50,28,29,20,12,6,17]})
print(data)
print(‘------‘)
# 创建样本数据

data.sort_values(‘智商‘, inplace=True)
data[‘range1‘] = np.arange(1,len(data)+1)
data.sort_values(‘每周看电视小时数‘, inplace=True)
data[‘range2‘] = np.arange(1,len(data)+1)
print(data)
print(‘------‘)
# “智商”、“每周看电视小时数”重新按照从小到大排序，并设定秩次index

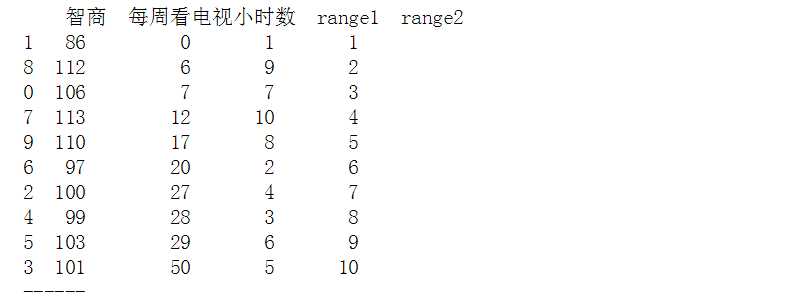
data[‘d‘] = data[‘range1‘] - data[‘range2‘]
data[‘d2‘] = data[‘d‘]**2
print(data)
print(‘------‘)
# 求出di，di2
n = len(data)
rs = 1 - 6 * (data[‘d2‘].sum()) / (n * (n**2 - 1))
print(‘Pearson相关系数为：%.4f‘ % rs)
# 求出rs

Pearson相关系数 - 算法

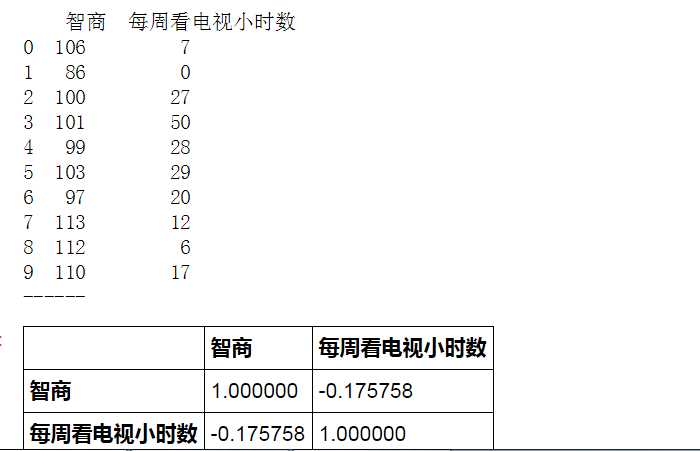
# Pearson相关系数 - 算法

data = pd.DataFrame({‘智商‘:[106,86,100,101,99,103,97,113,112,110],
                    ‘每周看电视小时数‘:[7,0,27,50,28,29,20,12,6,17]})
print(data)
print(‘------‘)
# 创建样本数据

data.corr(method=‘spearman‘)
# pandas相关性方法：data.corr(method=‘pearson‘, min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson