十循环链表的实现

Posted 2021-01-06 chenke1731

1、循环链表简介

概念上：

• 任意数据元素都有一个前驱和一个后继
• 所有的数据元素的关系构成一个逻辑上的环

实现上：

• 循环链表是一种特殊的单链表
• 尾结点的指针域保存了首结点的地址

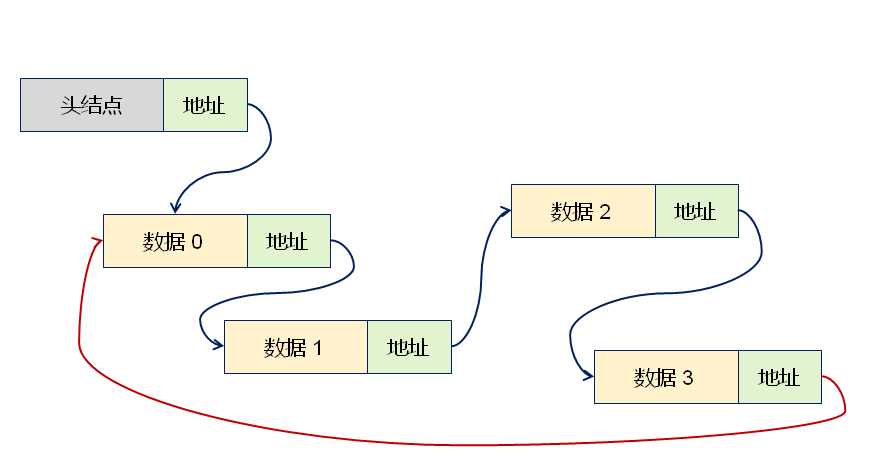
循环链表的继承层次结构

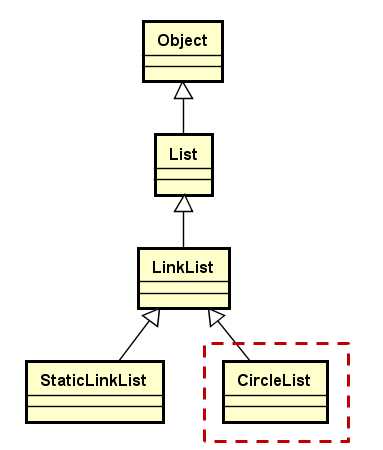
2、循环链表的实现思路

• 通过模板定义CircleList类，继承自LinkList类
• 定义内部函数last_to_first()，用于将单链表首尾相连
• 特殊处理：首元素的插入操作和删除操作
• 重新实现：清空操作和遍历操作

循环链表的实现要点：

• 插入位置为0时：插入的结点成为首结点
  • 头结点和尾结点均指向新结点
  • 新节点成为首结点插入链表
• 删除位置为0时：
  • 头结点和尾结点指向位置为1的结点
  • 安全销毁首结点

3、循环链表的具体实现

#ifndef CIRCLELIST_H
#define CIRCLELIST_H

#include "LinkList.h"


namespace DTLib
{
template <typename T>
class CircleList : public LinkList<T>
{
protected:
    typedef typename LinkList<T>::Node Node;

    int mod(int i) const
    {
        return (this->m_length == 0)? 0 : (i % this->m_length);
    }

    Node* last() const    // 获得指向最后一个结点的指针
    {
        return this->position(this->m_length-1)->next;
    }
    void last_to_first()
    {
        last()->next = this->m_header.next;
    }
public:
    bool insert(const T& e)
    {
        return insert(this->m_length, e);
    }
    bool insert(int i, const T& e)
    {
        bool ret = true;

        i = i % (this->m_length + 1);   // 对i进行归一化处理
        ret = LinkList<T>::insert(i, e);   // 用父类的insert函数来实现

        // 注意首尾相连
        if(ret && ( i == 0))
        {
            last_to_first();
        }


        return ret;
    }

    bool remove(int i)
    {
        bool ret = true;

        i = mod(i);
        if(i == 0)
        {
            Node* toDel = this->m_header.next;
            if(toDel != NULL)
            {
                this->m_header.next = toDel->next;
                this->m_length--;
                if(this->m_length > 0)  // 在还有元素的时候挪动
                {
                    last_to_first();
                    if(this->m_current == toDel)
                    {
                        this->m_current = toDel->next;
                    }
                }
                else
                {
                    this->m_header.next = NULL;
                    this->m_current = NULL;
                }
                this->destory(toDel);
            }
            else
            {
                ret = false;
            }
        }
        else
        {// 删除非首结点
            ret = LinkList<T>::remove(i);
        }

        return ret;
    }

    bool set(int i, const T& e)
    {
        return LinkList<T>::set(mod(i), e);
    }

    T get(int i) const
    {
        return LinkList<T>::get(mod(i));
    }

    bool get(int i, const T& e) const
    {
        return LinkList<T>::get(mod(i), e);
    }

    int find(const T& e) const
    {
        int ret = -1;
//        last()->next = NULL;    // 将尾结点的next指针置空，循环链表变成了单链表
//        ret = LinkList<T>::find(e);
//        last_to_first();
        // 但是这样就改变了循环链表的状态，不能这样干，因为find里面可能发生异常，循环链表就变成单链表了
        // 不是异常安全的
        // 需要重新实现find函数

        Node* slider = this->m_header.next;
        for(int i = 0; i < this->m_length; i++)
        {
            if(slider->value == e)
            {
                ret = i;
                break;
            }
            slider = slider->next;
        }
        // 异常安全，比较的时候就算发生异常，也不会造成循环链表的状态改变

        return ret;
    }

    void clear()
    {
        if(this->m_length > 0)
        {
//            last()->next = NULL;
//            LinkList<T>::clear();
            // 同样的问题，clear里面如果发生异常，不能保证异常安全性
            while( this->m_length > 1)
            {
                remove(1);  // 只要当前结点的长度大于1，就将结点1删除，直到所有元素删除
                // 不用remove(0)的原因是：考虑到效率问题
                // 每次remove(0)都会调用last_to_first等一大批操作
                // 删除非首结点就快很多
                // 所以选择删除结点1，这样最后就只会剩下结点0和首结点，再单独处理
            }
            if(this->m_length == 1)
            {
                Node* toDel = this->m_header.next;
                this->m_header.next = NULL;
                this->m_length = 0;
                this->m_current = NULL;
                this->destory(toDel);
            }
        }
    }

    // 重新实现遍历操作
    bool move(int i, int step)
    {
        return LinkList<T>::move(mod(i), step);
    }

    bool end()
    {
        return (this->m_length == 0) || (this->m_current == NULL);
    }

    ~CircleList()
    {
        clear();
    }

};

}

#endif // CIRCLELIST_H

4、循环链表的应用

约瑟夫环问题

已知n个人（以编号1，2，3...n分别表示）围坐在一张圆桌周围。从编号为k的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列。

// n 人数， s 第几号开始报数， m 报多少
void josephus(int n, int s, int m)
{
    CircleList<int> cl;
    for(int i = 1; i <= n; i++)
    {
        cl.insert(i);
    }

    cl.move(s-1, m-1);
    while(cl.length() > 0)
    {
        cl.next();
        cout << cl.current() << endl;
        cl.remove(cl.find(cl.current()));
    }
}

int main()
{
    josephus(41, 1, 3);


    return 0;
}

5、小结

循环链表是一种特殊的单链表

尾结点的指针域保存了首结点的地址

特殊处理首元素的插入操作和删除操作

重新实现清空操作和遍历操作