0阶 无符号指数哥伦布编码
Posted gaobw
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了0阶 无符号指数哥伦布编码相关的知识,希望对你有一定的参考价值。
指数哥伦布编码与哈夫曼编码一样都属于变长编码
但二者也有显著的区别:
1>信源相关性: 哈夫曼编码依赖于信源的概率分布,而指数哥伦布编码与信源无关
2>额外信息: 哈夫曼编码必须携带与该信源匹配的码表,指数哥伦布编码无需携带额外信息
h264官方协议文档中定义了4类指数哥伦布编码分为:
ue(v)无符号指数哥伦布编码 、se(v)有符号指数哥伦布编码、 te(v)截断指数哥伦布编码 和 me(v)映射指数哥伦布编码
下面我们截取了协议文档中 ue(v)无符号指数哥伦布编码的部分作为例子来分析,其他几种模式均是在此基础上 进行变换得来。
9 Parsing process
Inputs to this process are bits from the RBSP.
Outputs of this process are syntax element values.
This process is invoked when the descriptor of a syntax element in the syntax tables in subclause 7.3 is equal to ue(v), me(v), se(v), te(v) (see subclause 9.1), ce(v) (see subclause 9.2), or ae(v) (see subclause 9.3).
9.1 Parsing process for Exp-Golomb codes
This process is invoked when the descriptor of a syntax element in the syntax tables in subclause 7.3 is equal to ue(v), me(v), se(v), or te(v). For syntax elements in subclauses 7.3.4 and 7.3.5, this process is invoked only when entropy_coding_mode_flag is equal to 0.
Inputs to this process are bits from the RBSP.
Outputs of this process are syntax element values.
Syntax elements coded as ue(v), me(v), or se(v) are Exp-Golomb-coded. Syntax elements coded as te(v) are truncated Exp-Golomb-coded. The parsing process for these syntax elements begins with reading the bits starting at the current location in the bitstream up to and including the first non-zero bit, and counting the number of leading bits that are equal to 0. This process is specified as follows:
leadingZeroBits = ?1
|
for( b = 0; !b; leadingZeroBits++ ) b = read_bits( 1 ) The variable codeNum is then assigned as follows: |
(9-1) |
|
codeNum = 2leadingZeroBits ? 1 + read_bits( leadingZeroBits ) |
(9-2) |
where the value returned from read_bits( leadingZeroBits ) is interpreted as a binary representation of an unsigned integer with most significant bit written first.
Table 9-1 illustrates the structure of the Exp-Golomb code by separating the bit string into "prefix" and "suffix" bits. The "prefix" bits are those bits that are parsed in the above pseudo-code for the computation of leadingZeroBits, and are shown as either 0 or 1 in the bit string column of Table 9-1. The "suffix" bits are those bits that are parsed in the computation of codeNum and are shown as xi in Table 9-1, with i being in the range 0 to leadingZeroBits ? 1, inclusive.
Each xi can take on values 0 or 1.
Table 9-1 – Bit strings with "prefix" and "suffix" bits and assignment to codeNum ranges (informative)
|
Bit string form |
Range of codeNum |
|
1 |
0 |
|
0 1 x0 |
1..2 |
|
0 0 1 x1 x0 |
3..6 |
|
0 0 0 1 x2 x1 x0 |
7..14 |
|
0 0 0 0 1 x3 x2 x1 x0 |
15..30 |
|
0 0 0 0 0 1 x4 x3 x2 x1 x0 |
31..62 |
|
… |
… |
从上述表中我们可以看到 一个编码片段 分为3个部分 前缀0 、标志位bit1、后缀二进制数与前缀的位数相同。
计算公式为 codeNum = 2leadingZeroBits ? 1 + read_bits( leadingZeroBits )
如 0 0 0 1 0 1 1
前缀prefix 为 2^(leadingZeroBits = 3) -1 = 7
后缀surfix 0 1 1 = 0*2^2 + 1*2^1 +1*2^0 = 3
codeNum = prefix + surfix = 10
具体实现如下

// ExpColomb.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include <assert.h> typedef unsigned char UINT8; /* buf 为字节数组 bytePosition 为字节位置 bitPosition 为当前字节中 从左往右 的 bit位 的 位置 范围(0~7) 如 buf: 0 0 0 0 1 0 0 0, 1 1 0 0 0 1 0 0, 0 bytePosition: [ 0 ] [ 1 ] bitPosition: 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 */ static int get_bit_at_position(UINT8 *buf, UINT8 &bytePosition, UINT8 &bitPosition) { UINT8 mask = 0, val = 0; mask = 1 << (7 - bitPosition); val = ((buf[bytePosition] & mask) != 0);//获取当前bit位的值 if (++bitPosition > 7)//若大于7则进入下一个字节 { bytePosition++; bitPosition = 0; } return val; } static int get_uev_code_num(UINT8 *buf, UINT8 &bytePosition, UINT8 &bitPosition) { assert(bitPosition < 8); UINT8 bitVal = 0; int codeNum = 0,prefix = 0, surfix = 0,leadingZeroBits = 0; //获取前导0的个数 while (true) { bitVal = get_bit_at_position(buf, bytePosition, bitPosition); if (0 == bitVal) { leadingZeroBits++; } else { break; } } /*如 0 0 0 1 0 1 1 前缀prefix 为 2^(leadingZeroBits = 3) -1 = 7 后缀surfix 0 1 1 = 0*2^2 + 1*2^1 +1*2^0 = 3 codeNum = prefix + surfix = 10 */ prefix = (1 << leadingZeroBits) - 1; for (int bit_pos = leadingZeroBits-1; bit_pos >-1; bit_pos--) { bitVal = get_bit_at_position(buf, bytePosition, bitPosition); surfix += (1 << bit_pos)*bitVal; } codeNum = prefix + surfix; return codeNum; } int main() { UINT8 strArray[6] = { 0xA6, 0x42, 0x98, 0xE2, 0x04, 0x8A }; UINT8 bytePosition = 0, bitPosition = 0; UINT8 dataBitLength = sizeof(strArray) * 8; //数组的总bit数 int codeNum = 0; while ((bytePosition * 8 + bitPosition) < dataBitLength) { codeNum = get_uev_code_num(strArray, bytePosition, bitPosition); printf("ExpColomb codeNum = %d ", codeNum); } getchar(); return 0; }
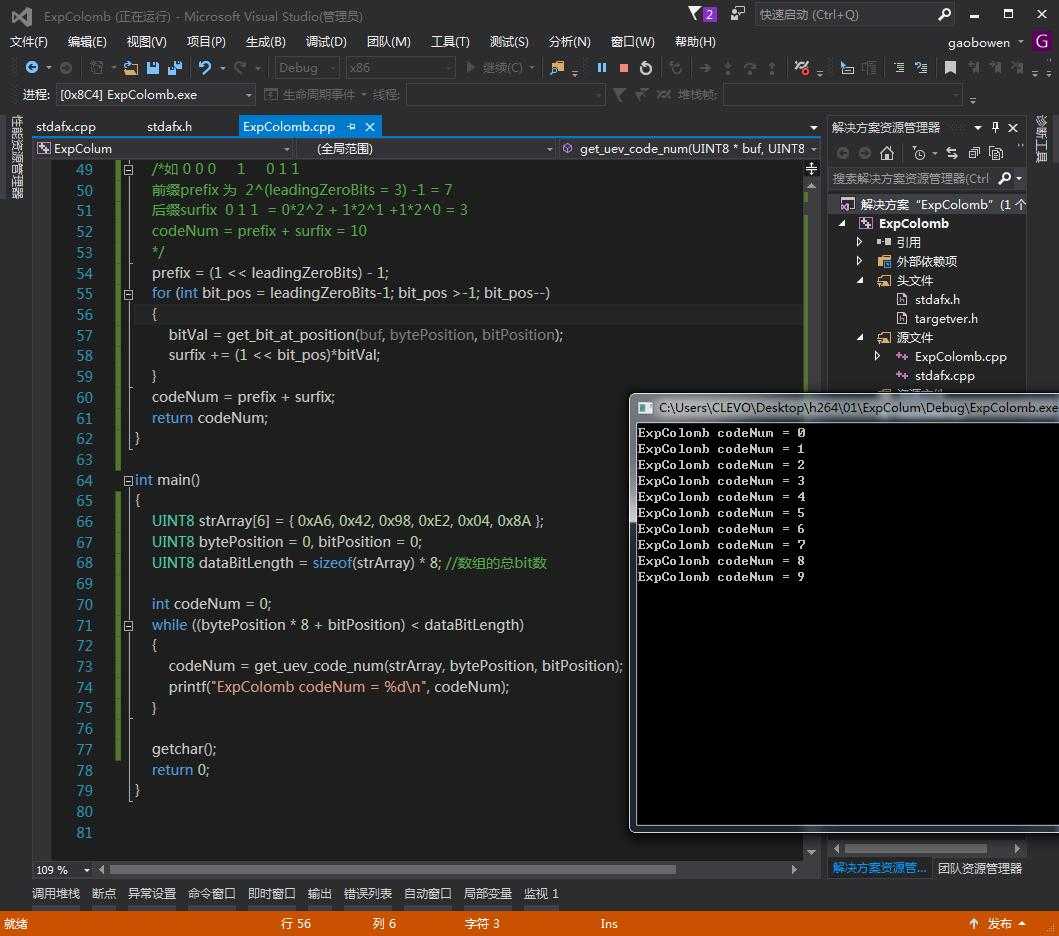
从运行结果可以看到 这里用6个字节 表示了从0到9的10个十进制数
标准协议文档中se(v) 有符号指数哥伦布编码如下
Table 9-3 – Assignment of syntax element to codeNum for signed Exp-Golomb coded syntax elements se(v)
|
codeNum |
syntax element value |
|
0 |
0 |
|
1 |
1 |
|
2 |
?1 |
|
3 |
2 |
|
4 |
?2 |
|
5 |
3 |
|
6 |
?3 |
|
k |
(?1)k+1 Ceil( k÷2 ) |
我们可以看出 se(v) 是由 我们上面计算的codeNum通过公式 (?1)codeNum+1 Ceil(codeNum÷2 ) 变换得来,
其中 ceil 为向上取整 ceil(1.5) = 2
映射指数哥伦布也是在得出codeNum的基础上,再通过查表得出具体数值 如:
(a) ChromaArrayType is equal to 0 or 3
|
codeNum |
coded_block_pattern |
|
|
|
Intra_4x4, Intra_8x8 |
Inter |
|
0 |
15 |
0 |
|
1 |
0 |
1 |
|
2 |
7 |
2 |
|
3 |
11 |
4 |
|
4 |
13 |
8 |
|
5 |
14 |
3 |
|
6 |
3 |
5 |
|
7 |
5 |
10 |
|
8 |
10 |
12 |
一个codeNum通过查表可以得到2个参数
以上是关于0阶 无符号指数哥伦布编码的主要内容,如果未能解决你的问题,请参考以下文章
