IOI1998Polygon

Posted 2021-01-06 kylara

题意翻译

题目可能有些许修改，但大意一致

多边形是一个玩家在一个有n个顶点的多边形上的游戏，如图所示，其中n＝4。每个顶点用整数标记，每个边用符号+（加）或符号*（乘积）标记。

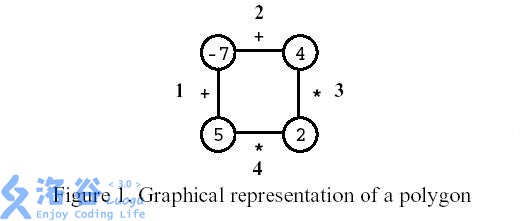
第一步，删除其中一条边。随后每一步：

选择一条边连接的两个顶点V1和V2，用边上的运算符计算V1和V2得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。

如图所示，玩家先移除编号为3的边。之后，玩家选择计算编号为1的边，然后计算编号为4的边，最后，计算编号为2的边。结果是0。

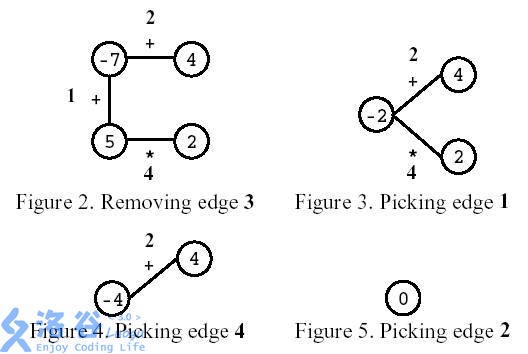
（翻译者友情提示：这里每条边的运算符旁边的数字为边的编号，不拿来计算）

编写一个程序，给定一个多边形，计算最高可能的分数。

输入格式

输入描述一个有n个顶点的多边形，它包含两行。第一行是数字n，为总边数。

第二行描述这个多边形，一共有2n个读入，每两个读入中第一个是字符，第二个是数字。

第一个字符为第一条边的计算符号(t代表相加，x代表相乘)，第二个代表顶点上的数字。首尾相连。

3 < = n < = 50

对于任何一系列的操作，顶点数字都在[-32768,32767]的范围内。

输出格式

第一行，输出最高的分数。在第二行，它必须写出所有可能的被清除后的边仍能得到最高得分的列表，必须严格递增。

输入输出样例

输入样例#1：

4
t -7 t 4 x 2 x 5

输出样例#1：

33
1 2
-------------------------------------------------------------------

这道题就用来练一下区间dp了
首先这是一个环状多边形，将其拆成链状处理

　　a[i+n]=a[i]; op[i+n]=op[i];//断链-> n*2

令 dp[l][r]表示以 l 为首项，以 r 为末项的链经过删边可以得到的最大值
然后，列出状态转移方程。这分为两部分：+和*

1.对于+,即op[i+1]==‘t‘;

　　dp[l][r]=max(dp[l][k]+dp[k+1][r],dp[l][r]);

2.对于*，情况稍微复杂：因为负负得正，所以我们还需要在转移时记录下
最小值[绝对值最大]，用f[i][j]记录

　　dp[l][r]=max( dp[l][r], max(dp[l][k]*dp[k+1][r],f[l][k]*f[k+1][r]) );

　　f[l][r]=min( f[l][r], min(dp[l][k]*dp[k+1][r],f[l][k]*f[k+1][r]) );

还要对边界进行处理，
令a[i]为第i个的初始值，那么：

　　dp[i][i]=f[i][i]=a[i];

同时，我们要先预处理长度为2的区间的答案

　　if(op[i+1]==‘t‘）

   　　dp[i][i+1]=f[i][i+1]=a[i]+a[i+1];

   if(op[i+1]==‘x‘)

      dp[i][i+1]=f[i][i+1]=a[i]*a[i+1];

最后！！！输入的时候注意令人智熄的scanf！！！！！
（查错两小时
因为本题中字符和数字在一行中输入，所以
直接写scanf("%s%d",&op[i],&a[i]);会导致读到的是空格
所以要写成scanf("%d
",&n); 和scanf("%s %d ",&op[i],&a[i]);
但是对于我来说，经常记不到的话，以后有同时输入字符和数字的时候，应该果断选择cin

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define N 120
 6 #define INF 0x7f7f7f7f
 7 #define ll long long
 8 using namespace std;
 9 ll f[N][N],dp[N][N];
10 int n,a[N];
11 char op[N];
12 ll ans=0;
13 int main()
14 {
15     scanf("%d",&n);
16     for(int i=1;i<=n;i++)
17     {
18        // scanf("%c %d ",&op[i],&a[i]);
19         cin>>op[i]>>a[i];
20         a[i+n]=a[i]; op[i+n]=op[i];//断链-> n*2
21     }
22     for(int i=1;i<=n*2;i++)
23         for(int j=i;j<=n*2;j++)
24             f[i][j]=INF,dp[i][j]=-INF;
25     for(int i=1;i<=n*2;i++)//预处len=2
26     {
27         if(op[i+1]==‘t‘)
28             dp[i][i+1]=f[i][i+1]=a[i]+a[i+1];
29         if(op[i+1]==‘x‘)
30             dp[i][i+1]=f[i][i+1]=a[i]*a[i+1];
31         dp[i][i]=f[i][i]=a[i];
32     }
33     for(int len=3;len<=n;len++)
34         for(int l=1;l<=n*2-len+1;l++)
35         {
36             int r=l+len-1;
37             for(int k=l;k<r;k++)
38             {
39                 if(op[k+1]==‘t‘)
40                 {
41                     dp[l][r]=max(dp[l][k]+dp[k+1][r],dp[l][r]);
42                     f[l][r]=min(f[l][k]+f[k+1][r],f[l][r]);
43                 }
44                 else//乘法可能有负负得正 故记录最大和最小值
45                 {
46                     dp[l][r]=max( dp[l][r], max(dp[l][k]*dp[k+1][r],f[l][k]*f[k+1][r]) );
47                     f[l][r]=min( f[l][r], min(dp[l][k]*dp[k+1][r],f[l][k]*f[k+1][r]) );
48                 }
49             }
50         }
51     for(int i=1;i<=n;i++)
52         //cout<<dp[i][i+n-1]<<" ";
53         ans=max(ans,dp[i][i+n-1]);
54     printf("%lld
",ans);
55     for(int i=1;i<=n;i++)
56         if(ans==dp[i][i+n-1])
57             printf("%d ",i);
58     return 0;
59 }
60 /*
61  scanf("%d
",&n);
62  scanf("%c %d ",&op[i],&a[i]);
63  和
64  scanf("%d",&n);
65  scanf("%c%d",&op[i],&a[i]);
66  */

ovo