P3935 Calculating (莫比乌斯反演)

Posted 2021-01-06 real-l

P3935 Calculating

题目描述

若xx分解质因数结果为(x=p_1^{k_1}p_2^{k_2}cdots p_n^{k_n}，令f(x)=(k_1+1)(k_2+1)cdots (k_n+1)f(x)=(k1?+1)(k2?+1)?(kn?+1)，)求(sum_{i=l}^rf(i))对(998244353)取模的结果。

输入输出格式

输入格式：

输入共一行，两个数，(l,r。)

输出格式：

输出共一行，一个数，为(sum_{i=l}^rf(i))对(998244353)取模的结果。

输入输出样例

输入样例#1：

2 4

输出样例#1：

7

说明

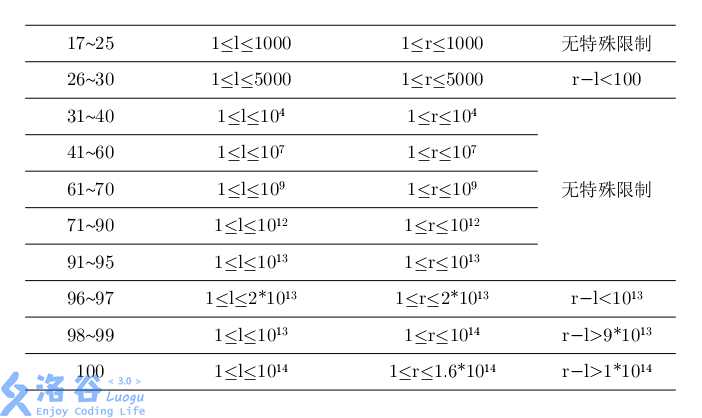
Solution

如果你做过一些莫比乌斯反演的题,那么这道题可以说就是一个整除分块的模板

首先我们需要知道一个定理:约数个数定理
设(f(x))为(x)的约数个数
[n=prod_{i=1}^k{p_i^{a_i}} o f(n)=prod_{i=1}^m{(a_i+1)}]
上述式子中,(p_i)为质数
证明:

由约数定义可知(p1^{a1})的约数有:(p1^0, p1^1, p1^2......p1^a1) ，共((a1+1))个;同理(p2^{a2})的约数有((a2+1))个......(pk^{ak})的约数有((ak+1))个。根据乘法原理答案就是上述式子

考虑一下题目所求,
[Ans=sum_{i=l}^{r}f(i)]
转换一下变成
[Ans=sum_{i=1}^rf(i)-sum_{i=1}^{l-1}f(i)]
对于(f(n)),我们可以认为
[f(n)=sum_{d|n}1]
令(Ans1=sum_{i=1}^rf(i)),由此推出
[Ans1=sum_{i=1}^rsum_{d|i}1]
更换枚举项,改为枚举i的因子
[Ans1=sum_{d=1}^rlfloorfrac{r}{d} floor]
同理求出(Ans2),然后用一下整除分块(O(sqrt n))预处理就可以了,不会的看一下我上面放的链接

Code

#include<bits/stdc++.h>
#define rg register
#define il inline
#define Min(a,b) (a)<(b)?(a):(b)
#define Max(a,b) (a)>(b)?(a):(b)
#define lol long long
using namespace std;

const lol mod=998244353;

void in(lol &ans) {
    ans=0; lol f=1; char i=getchar();
    while(i<'0' || i>'9') {if(i=='-') f=-1; i=getchar();}
    while(i>='0' && i<='9') ans=(ans<<1)+(ans<<3)+i-'0',i=getchar();
    ans*=f;
}

int main()
{
    lol ans1=0,ans2=0; lol n,m; in(n),in(m),n--;
    for(rg lol l=1,r,len;l<=n;l=r+1) {
        r=n/(n/l),len=r-l+1;
        ans1=(1ll*(ans1%mod+len%mod*(n/l)%mod)%mod)%mod;
    }
    for(rg lol l=1,r,len;l<=m;l=r+1) {
        r=m/(m/l),len=r-l+1;
        ans2=(1ll*(ans2%mod+len%mod*(m/l)%mod)%mod)%mod;
    }
    printf("%lld
",(ans2-ans1+mod)%mod);//注意这里,最后答案一定要(ans+mod)%mod,不然可能会出现负数
    return 0;
}

博主蒟蒻,随意转载.但必须附上原文链接

http://www.cnblogs.com/real-l/