最大的矩形面积 Maximal Rectangle

Posted 2021-01-06 timhy

2018-09-15 10:23:44

一、Largest Rectangle in Histogram

在求解最大的矩形面积之前，我们先讨论一条最大直方图面积的问题。

问题描述：

问题求解：

解法一、朴素解法，O(n ^ 2)。

解决的思路就是遍历一遍，如果当前的数比后一个数要小，那么当前的额数字肯定不可能是最大面积的右边界，遍历下一个数；

如果当前数比后一个大，那么假设当前的为右边界，向左进行遍历，计算面积最大值。

    public int largestRectangleArea(int[] heights) {
        if (heights.length == 0) return 0;
        int res = 0;
        for (int i = 0; i < heights.length; i++) {
            if (i == heights.length - 1 || heights[i] > heights[i + 1]) {
                int minHeight = heights[i];
                for (int j = i; j >= 0; j--) {
                    minHeight = Math.min(heights[j], minHeight);
                    res = Math.max(res, minHeight * (i - j + 1));
                }
            }
        }
        return res;
    }

解法二、使用堆栈，时间复杂度O(n)。

核心的思路是，寻找每个直方图的左边和右边第一个比他小的位置，然后计算其能达到的面积最大值，最后取max即可。

    public int largestRectangleArea(int[] heights) {
        if (heights.length == 0) return 0;
        int res = 0;
        Stack<Integer> stack = new Stack<>();
        int idx, leftMost, rightMost;
        for (int i = 0; i < heights.length; i++) {
            if (stack.isEmpty() || heights[i] >= heights[stack.peek()]) stack.push(i);
            else {
                rightMost = i;
                idx = stack.pop();
                while (!stack.isEmpty() && heights[stack.peek()] == heights[idx]) idx = stack.pop();
                leftMost = stack.isEmpty() ? -1 : stack.peek();
                res = Math.max(res, heights[idx] * (rightMost - leftMost - 1));
                i--;
            }
        }
        rightMost = stack.isEmpty() ? 0 :stack.peek() + 1;
        while (!stack.isEmpty()) {
            idx = stack.pop();
            leftMost = stack.isEmpty() ? -1 : stack.peek();
            res = Math.max(res, heights[idx] * (rightMost - leftMost - 1));
        }
        return res;
    }

 

二、Maximal Rectangle

问题描述：

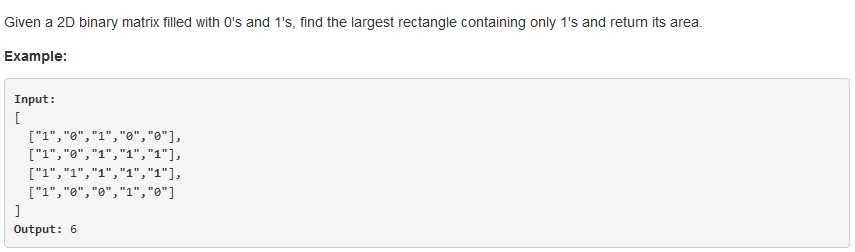
问题求解：

有个上一个问题的铺垫，这个问题就很好解决了，针对每一行，可以先求出其高度，然后再对每一行求最大最方图的面积，取max即可。

    public int maximalRectangle(char[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) return 0;
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] height = new int[m][n];
        int res = 0;
        for (int i = 0; i < n; i++) height[0][i] = matrix[0][i] - ‘0‘;
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == ‘0‘) height[i][j] = 0;
                else height[i][j] = 1 + height[i - 1][j];
            }
        }
        for (int i = 0; i < m; i++) {
            res = Math.max(res, fastHelper(height[i]));
        }
        return res;
    }

    private int helper(int[] nums) {
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i == nums.length - 1 || nums[i] > nums[i + 1]) {
                int minHeight = nums[i];
                for (int j = i; j >= 0; j--) {
                    minHeight = Math.min(minHeight, nums[j]);
                    res = Math.max(res, (i - j + 1) * minHeight);
                }
            }
        }
        return res;
    }

    private int fastHelper(int[] nums) {
        int res = 0;
        int idx, leftMost, rightMost;
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < nums.length; i++) {
            if (stack.isEmpty() || nums[i] >= nums[stack.peek()]) stack.push(i);
            else {
                rightMost = i;
                idx = stack.pop();
                while (!stack.isEmpty() && nums[idx] == nums[stack.peek()]) idx= stack.pop();
                leftMost = stack.isEmpty() ? -1 : stack.peek();
                res = Math.max(res, nums[idx] * (rightMost - leftMost - 1));
                i--;
            }
        }
        rightMost = stack.isEmpty() ? 0 : stack.peek() + 1;
        while (!stack.isEmpty()) {
            idx = stack.pop();
            while (!stack.isEmpty() && nums[idx] == nums[stack.peek()]) idx= stack.pop();
            leftMost = stack.isEmpty() ? -1 : stack.peek();
            res = Math.max(res, nums[idx] * (rightMost - leftMost - 1));
        }
        return res;
    }