bzoj 4603 平凡的骰子

Posted 2021-01-06 yyc-jack-0920

题目大意：

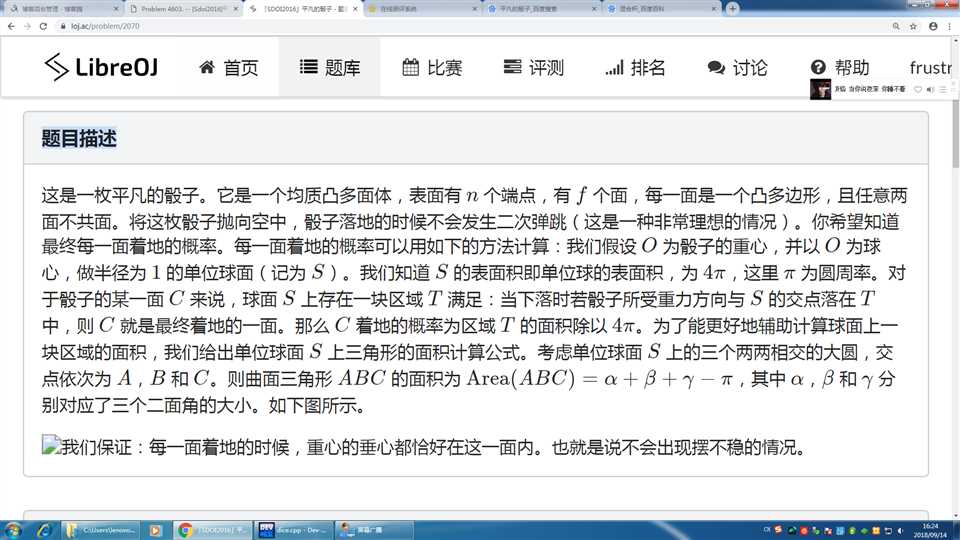
 思路：

首先我们需要求出整个凸多面体的重心

可以通过把多面体剖分为四面体 求出每个四面体的重心

四面体的重心为四个点的坐标和/4

对每个四面体的重心 加上它们体积的权 加权平均数即为整个的重心

（求每个四面体的体积可以用三个向量的混合积

因为给出了求凸面三角形的公式

因此一个凸面上凸N边形的公式为它的内角和-(N-2)*pi 

这样这个面的答案为面积/整个圆的表面积即4pi

（求二面角可以用叉积 求出两个法向量然后运用课内知识求出二面角

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #include<map>
10 #define inf 2139062143
11 #define ll long long
12 #define MAXN 200
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch==‘-‘) f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-‘0‘;ch=getchar();}
19     return x*f;
20 }
21 const double pi=acos(-1);
22 int n,m,alpha[MAXN][MAXN],num[MAXN];
23 struct Vector{double x,y,z;}p[MAXN];
24 Vector operator + (const Vector &a,const Vector &b) {return (Vector){a.x+b.x,a.y+b.y,a.z+b.z};}
25 Vector operator - (const Vector &a,const Vector &b) {return (Vector){a.x-b.x,a.y-b.y,a.z-b.z};}
26 Vector operator * (const Vector &a,const double &b) {return (Vector){a.x*b,a.y*b,a.z*b};}
27 Vector operator / (const Vector &a,const double &b) {return (Vector){a.x/b,a.y/b,a.z/b};}
28 Vector operator ^ (const Vector &a,const Vector &b) {return (Vector){a.y*b.z-a.z*b.y,a.z*b.x-a.x*b.z,a.x*b.y-a.y*b.x};}
29 double operator & (const Vector &a,const Vector &b) {return a.x*b.x+a.y*b.y+a.z*b.z;}
30 inline double len(Vector a) {return sqrt(a&a);}
31 inline double getV(Vector a,Vector b,Vector c) {return a&(b^c);}
32 inline double getA(Vector a,Vector b,Vector c)
33 {
34     Vector x=a^c,y=a^b;return acos(x&y/len(x)/len(y));
35 }
36 int main()
37 {
38     n=read(),m=read();Vector tmp,ctr;double x,vs=0.0,ans;
39     for(int i=1;i<=n;i++)
40         scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z);
41     for(int i=1;i<=m;i++)
42     {
43         num[i]=read();
44         for(int j=1;j<=num[i];j++) alpha[i][j]=read();
45     }
46     for(int i=1;i<=m;i++)
47         for(int j=2;j<num[i];j++)
48         {
49             tmp=p[alpha[i][1]]+p[alpha[i][j]]+p[alpha[i][j+1]];
50             x=getV(p[alpha[i][1]],p[alpha[i][j]],p[alpha[i][j+1]]);
51             vs+=x,ctr=ctr+tmp*x;
52         }
53     ctr=ctr/(vs*4);
54     for(int i=1;i<=n;i++) p[i]=p[i]-ctr;
55     for(int i=1;i<=m;i++)
56     {
57         ans=0;
58         for(int j=1;j<=num[i];j++) ans+=getA(p[alpha[i][j]],p[alpha[i][j!=1?j-1:num[i]]],p[alpha[i][j!=num[i]?j+1:1]]);
59         printf("%.7lf
",(ans-(num[i]-2)*pi)/(pi*4));
60     }
61 }

View Code