决策树分类算法小结

Posted 2021-01-05 jin-liang

引言

　　本文主要是对分类型决策树的一个总结。在分类问题中，决策树可以被看做是if-then规则的结合，也可以认为是在特定特征空间与类空间上的条件概率分布。决策树学习主要分为三个步骤：特征选择、决策树的生成与剪枝操作。本文简单总结ID3和C4.5算法，之后是决策树的修剪。

ID3算法

　　ID3算法和核心是：在决策树各级节点上选择属性时，用信息增益（information gain）作为属性的选择标准，具体做法是：检测所有的属性，选择信息增益最大的属性产生决策树节点，由该属性的不同取值建立分支，再对各分支循环调用该方法建立决策树节点的分支，直到所有子集仅包含同一类别为止。

信息增益

　　了解信息增益，首先介绍熵与条件熵的概念。

　　熵表示随机变量不确定性的度量。设$X$是一个取有限值的离散随机变量，其概率分布为：

$$p(X=x_i)=p_i$$

则随机变量 $X$ 的熵定义为:

$$H(X)=-sum_{i=1}^np_ilogp_i  ， i=1,2,n$$

由定义可知，熵只依赖于$X$的分布，而与$X$的取值无关。

熵越大，随机变量的不确定性越高，并且：

$$0leqslant{H(p)}leqslant{logn}$$

当随机变量只有两个取值时，例如0，1，则$X$的分布为：

 $$p(X=1)=p，p(X=0)=1-p，  0leqslant{p}leqslant1$$

熵为：

$$H(p)=-plog_2p-(1-p)log_2(1-p)$$

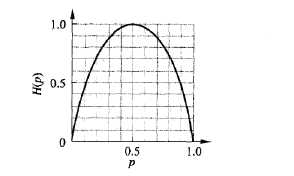
当$p=0$或$p=1$时，$H(p)=0$，随机变量完全没有不确定性，当$p=0.5$时，$H(p)=1$，熵取最大值，随机变量的不确定性最大。

 条件熵

 　　设随即变量$(X,Y)$，其联合概率分布为：

$$P(X=x_i,Y=y_i)=p_{ij},i=1,2,dots,n;j=1,2,dots,n$$

条件熵$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性，随机变量$X$给定的条件下随机变量$Y$的条件熵$H(Y|X)$，定义为$X$给定的条件下$Y$的条件概率分布的熵对$X$的数学期望：

$$H(Y|X)=sum_{i=1}^np_iH(Y|X=x_i)$$

这里，$p_i=P(X=x_i)$

信息增益

　　特征$A$对训练数据集$D$的信息增益，定义为集合$A$的经验熵$H(D)$与特征$A$给定条件下$D$的经验条件熵$H(D|A)$之差：

$$g(D,A)=H(D)-H(D|A)$$

小结

　　ID3算法就是在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂.

　　其核心是：决策树各级结点上选择属性时，用信息增益（information?gain）作为属性的选择标准，以使得在每一个非叶结点进行测试时，能获得关于被测试记录最大的类别信息。

　　其方法是：检测所有的属性，选择信息增益最大的属性产生决策树结点，由该属性的不同取值建立分支，再对各分支的子集递归调用该方法建立决策树结点的分支，直到所有子集仅包含同一类别的数据为止。最后得到一棵决策树。

C4.5算法

　　C4.5算法首先定义了“分裂信息”，即信息增益比：

$$g_R(D,A)=frac{g(D,A)}{H(D)}qquad$$

　　C4.5算法继承了ID3算法的优点，并在以下几方面对ID3算法进行了改进：?

• 1：用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足
• 2：能够完成对连续属性的离散化处理；?
• 3：能够对不完整数据进行处理。

决策树剪枝

　　决策树构造时，由于训练数据中的噪音或孤立点，许多分枝反映的是训练数据中的异常，使用这样的判定树对类别未知的数据进行分类，分类的准确性不高。因此试图检测和减去这样的分支，检测和减去这些分支的过程被称为树剪枝。树剪枝方法用于处理过分适应数据问题。通常，这种方法使用统计度量，减去最不可靠的分支，这将导致较快的分类，提高树独立于训练数据正确分类的能力。

　　树枝修剪包括事先修剪和事后修剪两种方法： 
　　（1）事前修剪方法：在决策树生成分支的过程，除了要进行基础规则的判断外，还需要利用统计学的方法对即将分支的节点进行判断，比如$chi^2$或统计信息增益，如果分支后使得子集的样本统计特性不满足规定的阈值，则停止分支；但是阈值如何选取才合理是比较困难的。 
　　（2）事后修剪方法：在决策树充分生长后，修剪掉多余的分支。根据每个分支的分类错误率及每个分支的权重，计算该节点不修剪时预期分类错误率；对于每个非叶节点，计算该节点被修剪后的分类错误率，如果修剪后分类错误率变大，即放弃修剪；否则将该节点强制为叶节点，并标记类别。产生一系列修剪过的决策树候选之后，利用测试数据（未参与建模的数据）对各候选决策树的分类准确性进行评价，保留分类错误率最小的决策树。 
　　除了利用分类错误率进行树枝修剪，也可以利用决策树的编码长度进行修剪。所谓最佳决策树是编码长度最短的决策树，这种修剪方法利用最短描述长度（MDL）原则来进行决策树的修剪。