二叉树的一些基本概念和求节点问题

Posted 2021-01-05 luza

最近写了很多笔试题,发现关于二叉树的好多概念还是没有完全理清,总结一下;

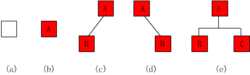
这是百度百科给的几种二叉树的类型:

(1)空二叉树——如图(a)；

 

(2)只有一个根结点的二叉树——如图(b)；

(3)只有左子树——如图(c)；

(4)只有右子树——如图(d)；

(5)完全二叉树——如图(e)

然后还有一点要说明的是二叉树不是树的特殊类型，他们相似也有很多不同点：

1. 树中结点的最大度数没有限制，而二叉树结点的最大度数为2；

2. 树的结点无左、右之分，而二叉树的结点有左、右之分。

 

先把树的概念和特点罗列一下：

树具有的特点有：

（1）每个结点有零个或多个子结点

（2）没有父节点的结点称为根节点

（3）每一个非根结点有且只有一个父节点

（4）除了根结点外，每个子结点可以分为多个不相交的子树。

几个常见的术语：

“双亲”——子树根上面的节点；“孩子”——上面那个节点下子树的根；就跟我们的亲属关系类似还有“兄弟”、“祖先”、“后裔”等说法很好理解。

结点的度：结点拥有的子树的数目

叶子结点：度为0的结点

分支结点：度不为0的结点

树的度：树中结点的最大的度

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1

树的高度：树中结点的最大层次

森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

 

二叉树一些性质，经常会有根据性质来的笔试题出现：

1：二叉树第i层上的结点数目最多为2^i-1(i>=1)

 

2：深度为k的二叉树至多有2^k-1个结点（k>=1）

 

3：包含n个结点的二叉树的高度至少为(log₂n)+1

 

4：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1

5：如果一棵完全二叉树的结点总数为n，那么叶子结点等于n/2（当n为偶数时）或者(n+1)/2（当n为奇数时）