多项式回归原理及在sklearn中的使用+pipeline

Posted 2021-01-05 wf-ml

相对于线性回归模型只能解决线性问题，多项式回归能够解决非线性回归问题。

拿最简单的线性模型来说，其数学表达式可以表示为：y=ax+b，它表示的是一条直线，而多项式回归则可以表示成：y=ax²+bx+c,它表示的是二次曲线，实际上，多项式回归可以看成特殊的线性模型，即把x²看成一个特征，把x看成另一个特征，这样就可以表示成y=az+bx+c,其中z=x²,这样多项式回归实际上就变成线性回归了。

下面介绍如何在sklearn中使用多项式回归

首先导入相应的库以及创造数据

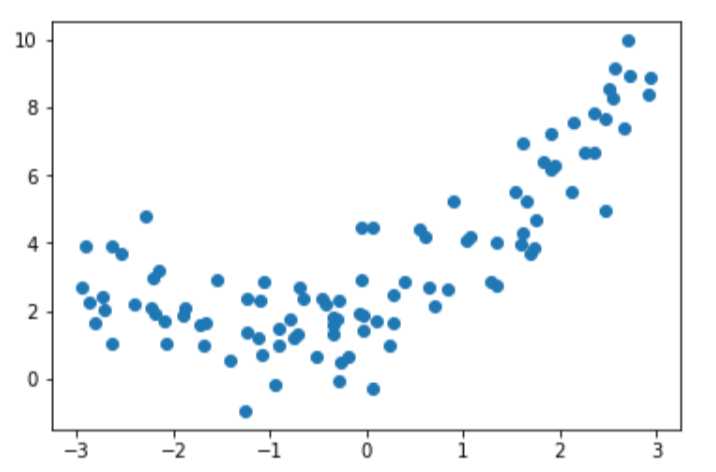
1 import numpy as np
2 import matplotlib.pyplot as plt
3 x = np.random.uniform(-3,3,size=100)
4 X = x.reshape(-1,1)
5 y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,100)

数据分布如图所示

接下来介绍sklearn中的PolynomialFeatures类：

由于多项式回归会产生x的高次项，所以需要对x进行处理，先上代码：

1 from sklearn.preprocessing import PolynomialFeatures
2 X = np.arange(1,11).reshape(-1,2)
3 poly = PolynomialFeatures(degree=2)
4 poly.fit(X)
5 X2 = poly.transform(X)

注意：此处的代码是单独的，跟上面的代码没有关系，我们先看一下X如下

它是一个5行2列的矩阵，再看一下X2：

它是一个5行6列的矩阵，它的第一列是X的第一列或者第二列的0次方，它的第二列和第三列就是X，第四列是X的第一列的平方，第五列是X的第一列与第二列的乘积，第六列是X的第二列的平方，用数学表达式：X = [X₁,X₂],X2=[1,X_1,,X₂,X₁²,X₁*X₂,X₂²]，在PolynomialFeatures中有一个超参数degree，它代表的就是多项式的最高次数。

在处理完X之后，我们就可以将得到的X2以及y送入线性模型去训练，由于在sklearn的线性模型是采用梯度下降法(后续会更新)求解的，故在训练之前需要对数据进行归一化，为了方便一条龙服务，我们使用sklearn中的Pipeline类，上代码：

1 from sklearn.preprocessing import StandardScaler
2 from sklearn.pipeline import Pipeline
3 poly_reg = Pipeline([
4     (‘poly‘,PolynomialFeatures(degree=2)),
5     (‘std_scaler‘,StandardScaler()),
6     (‘lin_reg‘,LinearRegression())
7 ])

说明一下Pipeline如何使用：Pipeline里面需要一个列表，列表里元素是一个个元组，每个元组代表对数据的处理，元组的第一个参数是处理的别名，随便取，第二个参数是处理的函数，如本例就是第一步构造高次项，第二步归一化，第三步使用线性回归，然后调用的时候sklearn会顺序执行这些步骤，这是sklearn的Pipeline的思想，代码如下：

1 poly_reg.fit(X,y)
2 y_predict = poly_reg.predict(X)
3 plt.scatter(x,y)
4 plt.plot(np.sort(x),y_predict[np.argsort(x)],color=‘r‘)
5 plt.show()

训练，预测并画出图示：

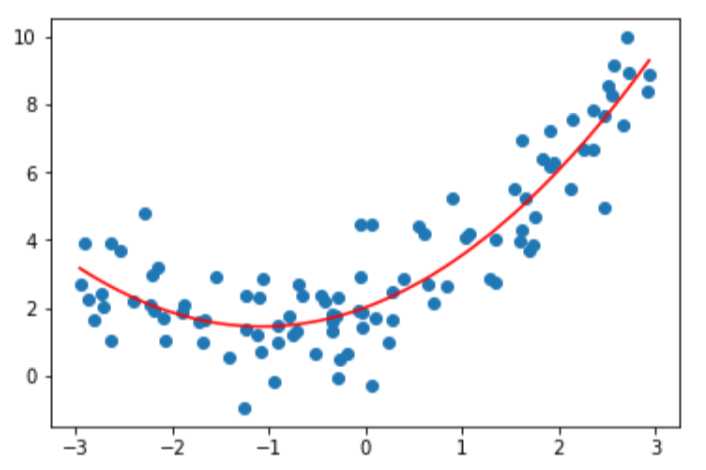
当然，degree参数不能设置太大，否则会过拟合。