递归&冒泡&装饰器

Posted 2021-01-05 palace

• 递归

在函数内部，可以调用其他函数。如果一个函数在内部调用自身本身，这个函数就是递归函数。

#lambda：
func = lambda x,y:9+x
参数：x,y
函数体:9+x
函数名:func

扩展：函数名可以当做参数传递 

函数名（）：执行函数

函数名：代指函数

def f1():
    return "F1"

#f1 ==>代指函数
#f1() ==>执行函数

示例：

def f3(arg):
    arg()

def x():
    print("xxx")

f3(x)
#打印结果：xxx

def f1():
    return "F1"

def f2(arg):
    arg()
    return "F2"

r = f2(f1)
print(r)
#打印结果:F2

# #f1 =>函数
# #f2 =>执行函数
# #f2(f1) =>执行f2函数，实际参数是f1函数

#斐波那契
def f(a1,a2):
if a1 > 100:
return
print(a1)
a3 = a1 + a2
f(a2,a3)
f(0,1)
#打印结果：
1
2
5
13
34
89

练习：写函数，利用递归获取斐波那契数列中的第 10 个数，并将该值返回给调用者。

def f(depth,a1,a2):
    if depth == 10:
        return a1
    a3 = a1 + a2
    r = f(depth+1,a2,a3)
    return r
ret = f(1,0,1)
print(ret)
#打印结果：34

 

冒泡排序：

    冒泡，原理是临近的数字两两进行比较，按照从小到大的顺序进行交换，这样交换一次之后，最大的数字就被交换到了最后一位。

    将列表中的数字按从小到大的顺序排列：

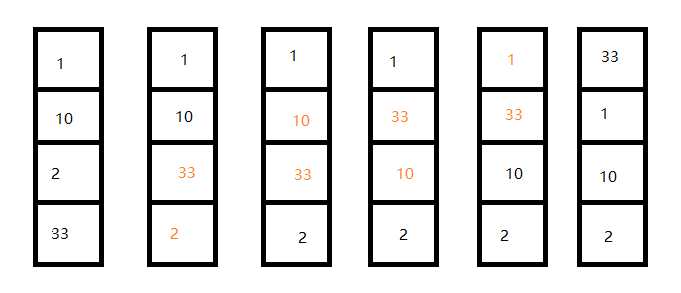
    然后再从头开始进行两两比较。

示例：

li = [33,2,10,1]
for j in range(1,len(li)):
    for i in range(len(li) - j):
        if li[i] > li[i + 1]:
            temp = li[i]
            li[i] = li[i + 1]
            li[i + 1] = temp
print(li)
#打印结果：[1, 2, 10, 33]

•  装饰器

    装饰器本质上是一个函数，该函数用来处理其他函数，它可以让其他函数在不需要修改代码的前提下增加额外的功能，装饰器的返回值也是一个函数对象。也就是说装饰器的作用就是为已经存在的对象添加额外的功能。 当使用@将装饰器附加到函数上时，就会调用此方法。

单层装饰器：

def outer(func):
    def inner():
        print("hello")
        r = func()
        print("end")
        return r
    return inner
@outer
def f1():
    print("F1")
f1()
#打印结果：
hello
F1
end


#1、执行outer函数，是将下面的函数名，当做outer函数的参数
#2、将outer的返回值重新赋值给f1，意思就是f1 = outer的返回值

 

双层装饰器：

注：对参数数量不确定的函数进行装饰，参数用（*args,**kwargs），自动适应参数数量。

和单层装饰器原理一样，只是在原有基础上又多了一个装饰器。示例：

def outer1(func):
    def inner(*args,**kwargs):
        print("123")
        ret = func(*args,**kwargs)
        print("123")
        return ret
    return inner
def outer2(func):
    def inner(*args,**kwargs):
        print("456")
        ret = func(*args,**kwargs)
        print("456")
        return ret
    return inner
@outer1
@outer2
def f():
    
    return "ok"

r = f()
print(r)

#打印结果：
123
456
456
123
ok

# 1、执行outer2函数，将f作为outer2函数的参数，将f赋值给func
# 2、得到返回值inner，重新赋值给f：f = inner  ==>  f() = inner()
# 3、执行outer1函数，将整个inner函数作为outer1函数的参数
# 4、得到返回值inner，再重新赋值给f：f == inner  ==> f() = inner()
# 5、因为装饰器只有两层，就不用再执行下一个装饰器函数，如果更多层就继续循环以上程序过程
# 6、下面就执行最终的inner函数，执行func函数时，就是执行最原始的f函数