哈夫曼编码--贪心策略

Posted 2021-01-05 acmblog

哈夫曼编码还是在暑假时候看的，那时候并没有看懂因为比较菜（虽然现在也是很菜的），在《趣学算法》一书中这个问题讲解十分到位，我这篇博客真的是难以望其项背，只能对其进行一点借鉴和摘抄吧

哈夫曼编码是一棵树，权值越大的节点越靠近树根，越小的节点就越远离树根，从他的定义来看，首先想到的应该是贪心策略吧，没错就是贪心算法

虽然说是贪心算法，但是还要知道它 的实现方式啊，他的贪心策略是：每次从树的集合中取出没有双亲且权值最小的两棵树作为左右子树，并合并他们

步骤 ：

　　1 ：确定合适的数据结构（要知道他的左右子树，双亲，权值）

　　2：初始化，构造n颗节点为n的字符单节点树集合T={t1,t2,t3,t4···········tn}，并且每棵树只有树根

　　3：如果集合中只剩下一棵树，那么哈夫曼树就构造成功，直接跳转到步骤6，否则就是从集合中继续拿出没有双亲的左右子树x，y，并将它们合并到一颗z树中，

　　　　z的权值为左右子树权值之和

　　4：从T集合中删除x，y 把新树z加入到集合T中

　　5：重复步骤3~4

　　6：约定左分支上的编码都是0，有分支上的编码都是1，从叶子节点开始逆序求出树的编码

图解：（这儿就直接调用这本书上的图片吧，是在太懒不想画图）

　　

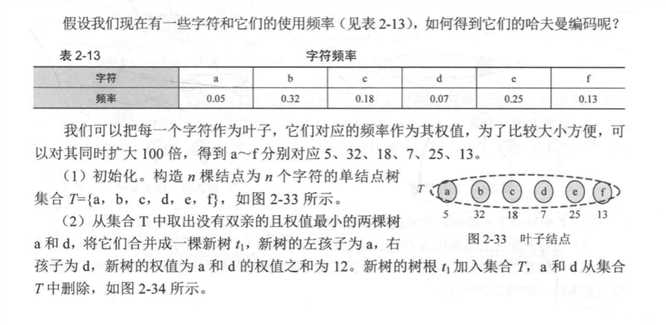
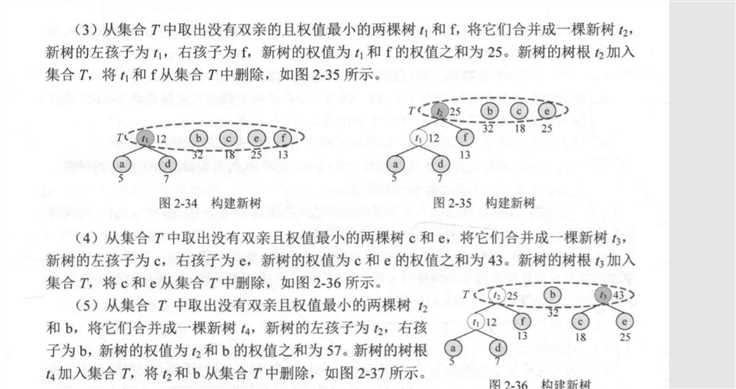
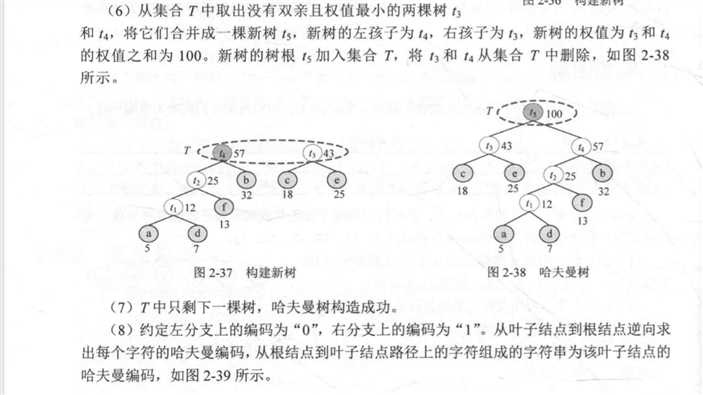
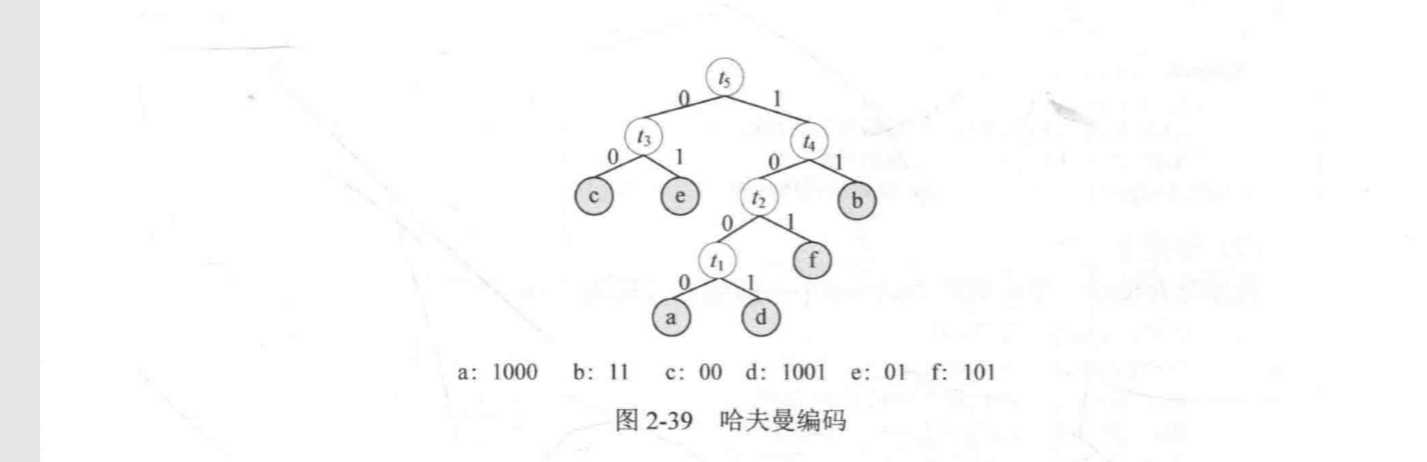
代码的实现：

#include<bits/stdc++.h>
using namespace std;
#define MAXBIT 100
#define MAXVALUE 10000
#define MAXLEAF 30
#define MAXNODE MAXLEAF*2-1
typedef struct{
    double weight;
    int parent;
    int lchild;
    int rchild;
    char value;
}HNodeType;//?¨ò?μ?ê??úμ?·?±eóDè¨??￡????×?úμ?￡?×óóòo￠×ó￡??1óD′ú±íμ?×?·? 
typedef struct{
    int bit[MAXBIT];
    int start;
}HCodeType;//?aê?±à???á11ì? 
HNodeType HuffNode[MAXNODE];//?úμ??á11ì?êy×é 
HCodeType HuffCode[MAXLEAF];//±à???á11ì?êy×é 
/*?ó??à′?aê?11?ì1t·ò?üê÷*/
void HuffmanTree(HNodeType HuffNode[MAXNODE],int n)
{
    /*i,jê??-?·±?á?￡?m1,m2ê?×?D?μ?è¨?μ
    x1,x2ê?1t·ò?üê÷×?D?è¨?μ??ó|μ?Dòo?
    */
    int i,j,x1,x2;
    double m1,m2;
//    3?ê??ˉ?úμ? 
    for(i=0;i<2*n-1;i++)
    {
        HuffNode[i].lchild=-1;
        HuffNode[i].parent=-1;
        HuffNode[i].rchild=-1;
        HuffNode[i].weight=0;
    }
    for(i=0;i<n;i++)
    {
        cout<<"Please enter the value of every Node "<<i+1<<endl;
        cin>>HuffNode[i].value>>HuffNode[i].weight;
    }
//    11?ì1t?￥?üê÷
    for(i=0;i<n-1;i++)
    {//òa?-?·n-1′? 
        m1=m2=MAXVALUE;
        x1=x2=0;
    //?????aê??ò×?D?μ?á????μ
        for(j=0;j<n+i;j++)
        {
            if(HuffNode[j].weight<m1&&HuffNode[j].parent==-1)
            {
                m2=m1;
                x2=x1;
                m1=HuffNode[j].weight;
                x1=j;
            }
            else if(HuffNode[j].weight<m2&&HuffNode[j].parent==-1)
            {
                m2=HuffNode[j].weight;
                x2=j;
            }
        }
        HuffNode[x1].parent=n+i;
        HuffNode[x2].parent=n+i;
        HuffNode[n+i].weight=m1+m2;
        HuffNode[n+i].lchild=x1;
        HuffNode[n+i].rchild=x2;
        cout<<"x1.weight and x2.weight in round "<<i+1<<"	"
            <<HuffNode[x1].weight<<"	"<<HuffNode[x2].weight<<endl;//ó?óú2aê?
         
    }
}
void HuffmanCode(HCodeType HuffCode[MAXLEAF],int n)
{
    HCodeType cd;
    int i,j,c,p;
    for(i=0;i<n;i++)
    {
        cd.start=n-1;
        c=i;
        p=HuffNode[c].parent;
        while(p!=-1)
        {
            if(HuffNode[p].lchild==c)
                cd.bit[cd.start]=0;
            else 
                cd.bit[cd.start]=1;
            cd.start--;
            c=p;
            p=HuffNode[c].parent;
        }
        for(j=cd.start+1;j<n;j++)
            HuffCode[i].bit[j]=cd.bit[j];
        HuffCode[i].start=cd.start;
    }
}
int main()
{
    int i,j,n;
    cout<<"Please enter n"<<endl;
    cin>>n;
    HuffmanTree(HuffNode,n);
    HuffmanCode(HuffCode,n);
    for(i=0;i<n;i++)
    {
        cout<<HuffNode[i].value<<": Huffman Code is: ";
        for(j=HuffCode[i].start+1;j<n;j++)
        {
            cout<<HuffCode[i].bit[j];
        }
        cout<<endl;
    }
    return 0;
}