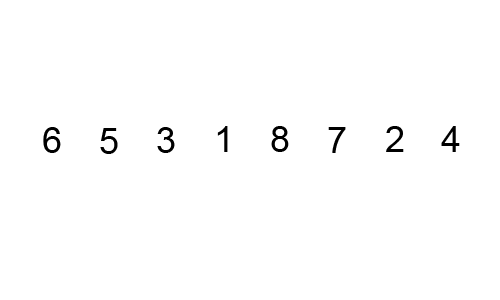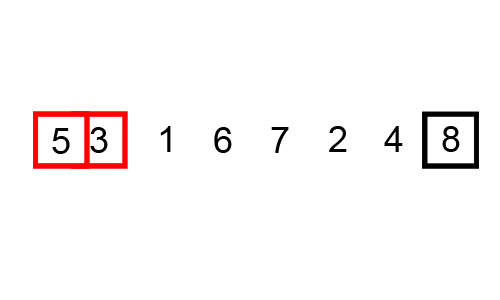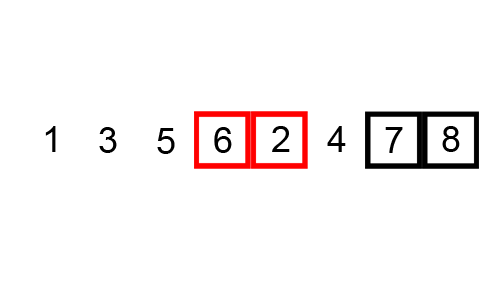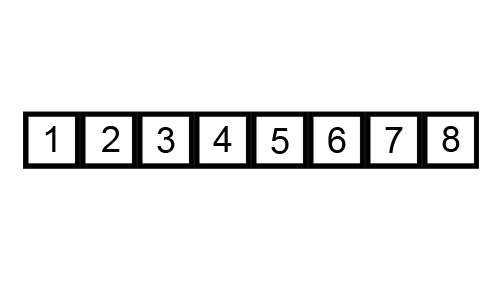数据结构与算法从零开始系列：冒泡排序选择排序插入排序希尔排序堆排序快速排序归并排序基数排序

Posted 2021-01-05 wangfengxia

欢迎Star，本文的所有示例源码都在Github:https://github.com/AndroidHensen/Arithmetic

本篇内容包含

• 排序的介绍
• 排序的C的实现
• 排序的Java的实现
• 排序的时间复杂度的计算

---

1、基本思想：

两个数比较大小，较大的数下沉，较小的数冒起来

2、实现步骤：

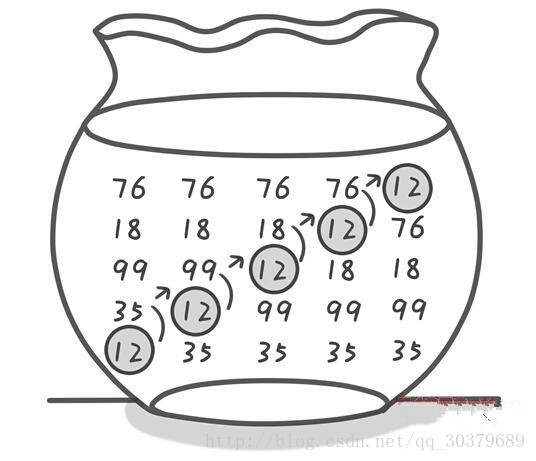
这张图就是将数字12，35，99，18，76竖起来

• 第一次：从底部有一个气泡，圈住12并且和35对比，如果比上面小就交换，气泡往上升
• 第二次：12和99对比，如果比上面小就交换，气泡往上升
• 第三次：重复上面的操作，最后可以把12排到最上面

3、这张图模拟了冒泡排序的整个过程

• 第一个红色框表示气泡
• 两个红色框表示比较大小
• 黑色框表示已经排好的数字
• 最后排成有序的数字

1、程序优化：

• 这里加了一个flag作为优化程序的条件，如果程序未进入内循环，说明数字已经排序好了，后面的比较也就没有意义了，直接程序结束

2、实现口诀：

• 两数相抱转个圈

3、易犯错误：

• 忘记添加优化flag

1、我们从代码分析，可以知道有两个循环

1. 外循环：执行(n-1)次，当最坏的情况下，会执行n次，虽然最后一次(i < n)不通过，但还是算一次，其中里面有一条赋值语句
2. 内循环：在(i=1,2,3…n-1)，执行(n-i)次，即(n-1,n-2…1)，其中有四条赋值语句

2、那么就可以计算出各自复杂度

1. 外循环：最坏情况下是(1 x n)次
2. 内循环：通过等差数列求和公式，(n-1+n-2+…1)=n^2/2

3、根据推导大O阶规则来进行推导

1. 用常数1来取代运行时间中所有加法常数
2. 修改后的运行次数函数中，只保留最高阶项
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数

4、得到的冒泡排序的复杂度的大O表示法为

(1xn)+(n^2/2) ≈ n^2=O(n^2)

---

1、基本思想：

• 让第一个数与后面的所有数一个个比较，找出最小的数，将最小的数跟第一个数交换
• 接着从第二个数开始，继续上面的操作

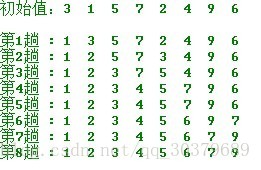
2、实现步骤：

1、注意点：

• 用语言实现排序的时候，只是记录着最小值的下标，接着用最小值的下标继续和后面的数进行比较，这是和思路不同的地方

2、实现口诀：

• 角标互换

3、易犯错误：

• 忘记添加角标判断

1、我们从代码分析，可以知道有两个循环

1. 外循环：执行(n-1)次，当最坏的情况下，会执行n次，虽然最后一次(i < n)不通过，但还是算一次，其中里面有四条赋值语句
2. 内循环：在(j=1,2,3…n-1)，执行(n-i)次，即(n-1,n-2…1)，其中有一条赋值语句

2、那么就可以计算出各自复杂度

1. 外循环：最坏情况下是(4 x n)次
2. 内循环：通过等差数列求和公式，(n-1+n-2+…1)=n^2/2

3、复杂度的大O表示法为

(4xn)+(1x(n^2/2)) ≈ n^2=O(n^2)

1、基本思想：

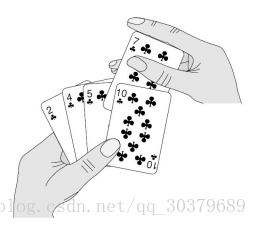
• 其实就是你玩扑克牌的时候，排序你自己的牌的思路
• 从后面抽出牌，插入到前面的牌中

2、实现步骤：

• 初始值：1, 4, 8, 3, 2, 9, 5, 0, 7, 6
• 第一次：抽出牌4，与1对比，发现比它大，不交换
• 第二次：抽出牌8，与4对比，发现比它大，不交换
• 第三次：抽出牌3，与8对比，发现比它小，交换，继续与前面一个数比，与4对比，发现比它小，交换，继续与前面一个数比，与1对比，发现比它大，不交换
• 第四次：重复上面步骤，完成扑克牌排序

1、实现口诀：

• 扑克牌往回插

2、易犯错误：

• 忘记退出的break

1、我们从代码分析，可以知道有两个循环

1. 外循环：执行(n-1)次，当最坏的情况下，会执行n次，虽然最后一次(i < n)不通过，但还是算一次
2. 内循环：在(i=0,1,2,3…n-2)，执行(n-i-1)次，即(n-1,n-2…1)，其中有三条赋值语句

2、那么就可以计算出各自复杂度

1. 外循环：最坏情况下是(n)次
2. 内循环：通过等差数列求和公式，3x(n-1+n-2+…1)=(3x(n^2/2))

3、复杂度的大O表示法为

(n)+(3x(n^2/2)) ≈ n^2=O(n^2)

1、基本思想：

• 先对所有的数进行分组
• 对分组的数进行插入排序

2、实现步骤：

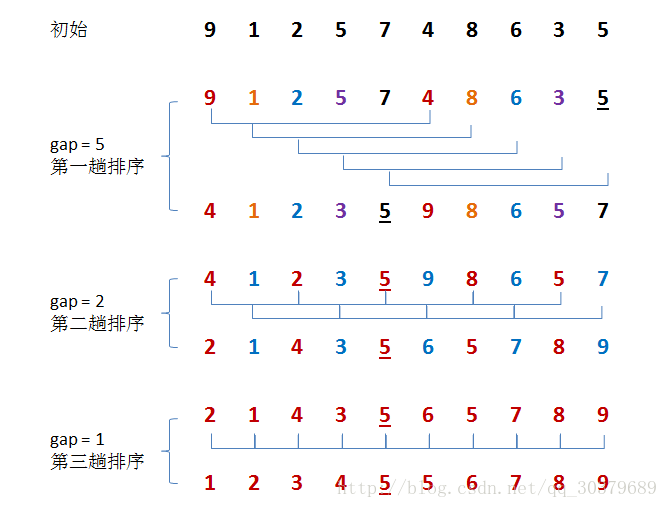
这张图就是将数字9，1，2，5，7，4，8，6，3，5，按分量（数的个数/2）进行分组，然后在各分组中进行插入排序

• 第一次：按分量5分成5组，在组中分别进行插入排序
• 第二次：按分量2分成5组，在组中分别进行插入排序
• 第三次：按分量1分成5组，在组中分别进行插入排序

1、实现口诀：

• 分组，插入

2、易犯错误：

• 忘记添加结束break

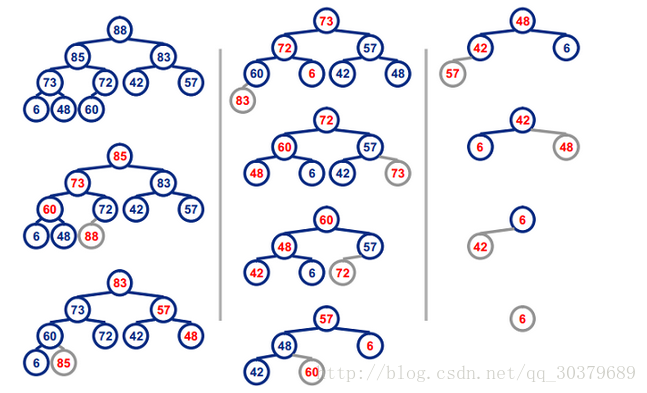
1、基本思想：

• 整理小顶堆
• 将小顶堆a[0]和a[i]和互换
• 将换下来后的a[i]取出，即最大数
• 继续整理小顶堆

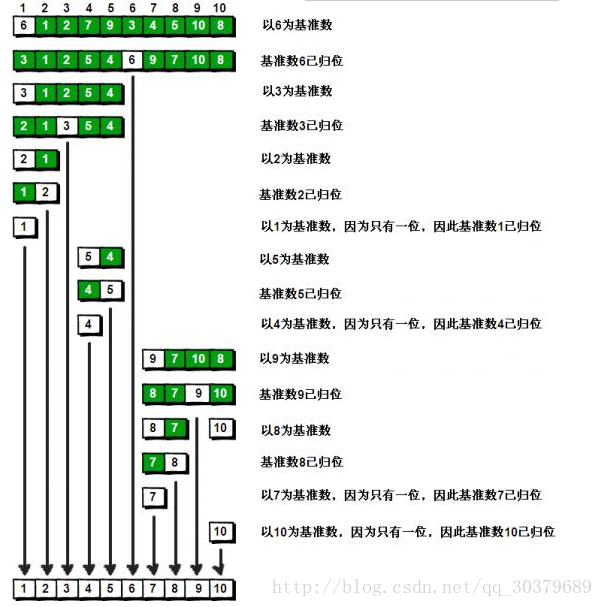
1、基本思想：

• 以第一个数（a）为基准
• 分别在头部和尾部添加指针
• 右边指针先开始，遇到比a小的数则停止
• 左边指针后开始，遇到比a大的数则停止
• 交换右边和左边的指针数
• 重复上述步骤，直到两指针相等
• 交换a与两指针指向的数

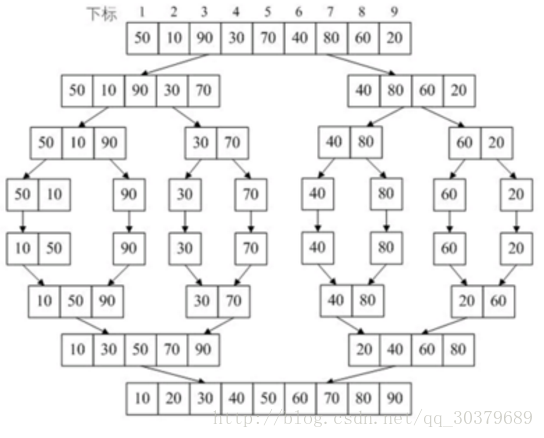
1、基本思想：

• 先将需要排序的数，按中点进行分组
• 重复分组，直到分到的组不能再分
• 比较最后分开的两个组
• 哪个组的数小，就取谁，取了后就在对应数列中删除这个数
• 重复取数，直到两组的数被完全取出，合并取出来的所有数
• 重复上述比较、取数、合并的步骤，最后合并成有序数组

在学习基数排序之前，必须要知道桶排序，所以先简单的学习一下桶排序

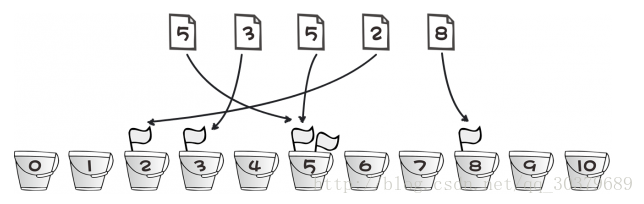
1、基本思想：

• 首先创建数组A[MaxValue]
• 将每个数放到相应的位置上，即数的值和索引相等的位置
• 最后遍历数组，即为排序后的结果

1、基本思想：

• 将每个数的个位开始进行桶排序
• 排序完成后，桶按顺序输出中年女装品牌
• 将排序好个位的数，进行十位开始桶排序
• 排序完成后，桶按顺序输出
• 重复上述步骤，直到最高位进行桶排序，按顺序输出即为结果

 

排序类型	时间复杂度
冒泡排序	O(n^2)
选择排序	O(n^2)
插入排序	O(n^2)
希尔排序	O(n^1.5)
堆排序	O(N*logN)
快速排序	O(N*logN)
归并排序	O(N*logN)
基数排序	O(d(n+r))