95. Unique Binary Search Trees II
Posted mozi-song
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了95. Unique Binary Search Trees II相关的知识,希望对你有一定的参考价值。
题目
Given an integer n, generate all structurally unique BST‘s (binary search trees) that store values 1 ... n.
Example:
Input: 3
Output:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST‘s shown below:
1 3 3 2 1
/ / / 3 2 1 1 3 2
/ / 2 1 2 3
思路
记fn为1至n组成的BST的集合。对该BST,根的值有n种情况。对每一个根值i,左树为1至i-1,即问题fi-1。右树为i+1至n,即问题fn-i,但每个节点要+i。即
fn = ∑ fi-1 * fn-i (i=1...n)
注: 此处答案要求是一个List,所以*不代表数学的乘积而是将左右树做交叉结合
代码
1 class Solution { 2 public List<TreeNode> generateTrees(int n) { 3 List<TreeNode>[] dp = new List[n + 1]; 4 dp[0] = new ArrayList<>(); 5 if(n == 0) return dp[0]; 6 dp[0].add(null); 7 8 for(int i = 1; i <= n; i++){ 9 dp[i] = new ArrayList<>(); 10 for(int j = 1; j <= i; j++){ 11 int left = j - 1, right = i - j; 12 for(TreeNode leftTree : dp[left]) 13 for(TreeNode rightTree : dp[right]){ 14 TreeNode root = new TreeNode(j); 15 root.left = clone(leftTree, 0); 16 root.right = clone(rightTree, j); 17 dp[i].add(root); 18 } 19 } 20 } 21 return dp[n]; 22 } 23 24 private TreeNode clone(TreeNode x, int offset){ 25 if(x == null) 26 return null; 27 TreeNode result = new TreeNode(x.val + offset); 28 result.left = clone(x.left, offset); 29 result.right = clone(x.right, offset); 30 return result; 31 } 32 }
复杂度(大致分析)
设问题n对应的List长度为ln,由于每次都从1到n开始填表,则问题n的时间复杂度Tn大致为
Tn = 1*l1 + 2*l2 + ...+ n*ln (1)
其中乘以n的原因是:ln中的每一颗树都是通过克隆子问题的树形成的。对于一个n个节点的树,克隆的时间为O(n)。
对于每一个ln,考虑到其左右子树的不同大小,又有
ln = ∑ lj-1 * ln-j (j=1...n) (2)
即l2 = l0*l1 + l1*l0, l3 = l0*l2 + l1*l1 + l2*l0,...
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ... |
| ln | 1 | 1 | 2 | 5 | 14 | 42 | ... | ... |
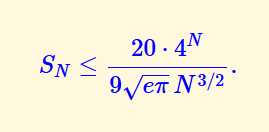
我们的和里还有一个因子n(式1),大致可以确定Tn大概为O(4n/nk)的样子吧,至于k是几不会算(据上式,起码有k<3/2...)……
实际上,卡塔兰数的渐进表示大致为
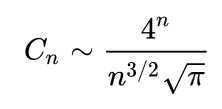
与上述估算的Tn大致相同(最大的差别在于那个clone所耗费的因子n),也就是说dp算法本身比穷举法的时间复杂度差一点,拖了一点后腿……
不过这个问题用穷举法确实没想到intuitive的算法,backtracking的话估计浪费更严重,dp应该算是比较简洁又复杂度还可以的算法……
以上是关于95. Unique Binary Search Trees II的主要内容,如果未能解决你的问题,请参考以下文章