[Codeforces Round #194 (Div. 2)] Secret 解题报告 （数学）

Posted 2021-01-05 xxzh

题目链接：http://codeforces.com/problemset/problem/334/C

题目：

题目大意：

给定数字n，要求构建一个数列使得数列的每一个元素的值都是3的次方，数列之和S大于n，且删掉数列中的任意一个元素数列之和都会小于n，最小化这个数列的长度

题解：

我们考虑从小到大枚举k，取最小的k，使得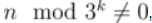，答案就是$n/3^k+1$

为什么呢？

我们考虑一个合法的数列，其中最小的元素是A，那么S一定是A的倍数。假设n是A的倍数，又S>n，那么S-A>=n，这样的话去掉A这个数列依旧大于等于n，数列就不合法了。

所以我们有n一定不是A的倍数。

于是我们从小到大枚举A的大小，直到找到最小的A满足n不是A的倍数，那么就直接用面值为A的硬币就可以了。

也许有为什么不用更大的满足n不是A的倍数的A的疑惑，其实更大的话也都可以表示成最小的A的倍数，那显然是没有用A优的

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

long long n;
int main()
{
    cin>>n;
    while(n%3==0)
    {
        n/=3;
    }
    cout<<n/3+1<<endl;
    return 0;
}