Codeforces Round #500 (Div. 2) 游记

Posted 2021-01-05 lyfoi

A Piles With Stones

题意

有(N)堆石子，任意个人。每个人可以把一堆石子中的一个石子移动到另一堆，或者是拿走一堆石子。现在给你石子一开始的情况与这些人进行操作后的情况，问是否合法。

思路

此题看上去不简单，但是你可能在几秒内想出一个结论，那就是：无论这些人怎么移动，都没有办法使得石子数量增多！那么做法就简单了，如果石子数量比没改动前的多，那么就不合法了。

Code

#include<iostream>
using namespace std;
int sum1=0,sum2=0;
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int t;
        cin>>t;
        sum1+=t;
    }
    while(n--)
    {
        int t;
        cin>>t;
        sum2+=t;
    }
    if(sum2>sum1)
        cout<<"No"<<endl;
    else
        cout<<"Yes"<<endl;
    return 0;
}

B And

题意

给你(N)个数和一个(X)，每次你可以选一个数改变为这个数(And) (X)。这个操作可以进行任意次，问至少将几个数进行与运算才能使得至少有两个数相等，注意：如果生产后的数和原来一样，那么只算一个。

思路

还是一道看上去很难的题，这道题我的思路非常非常的特殊。

要做这道题，我们首先要知道这些定理和结论：

• 一个数无论与另一个数进行与运算几次，得出的值都是一个数。

• 求最小的步数，只要我们满足有两个数想等了，那么就可以判断输出了。也就是说，只有(4)种情况：(-1,0,1,2)。(-1)为不可能，(0)为本来就有至少(2)个相等的，(1)为有一个数进行一次与运算后等于了一个在原序列出现过的数，(2)为有(2)个数进行与运算后等于了一个没有在原序列出现过的数。

• 如果一个数经过与运算后能得到自己，那就别进行运算。

根据上面两个加黑为要点，我们可以分类讨论。有(2)个坑，有的地方我会在代码里注释。

Code

#include<bits/stdc++.h>
using namespace std;
int n,x,ans=-1,a[100100],times[100100];
//times[i]=1代表本身与与运算后一样的一次,=2代表一个数进行了与运算产生了一个新的数 
int main()
{
    cin>>n>>x;
    for(int i=1;i<=n;i++)//先处理自己本身不变的情况 
    {
        cin>>a[i];
        if (times[a[i]]) 
            return cout<<0<<endl,0;
        times[a[i]]=1; //出现过一次了 
    } 
    for(int i=1;i<=n;i++)//再处理进行与运算的情况 
    {
        int b=a[i]&x;
        if(times[b]==1&&a[i]!=b)//注意着里a[i]必须不能与b相等 
            return cout<<1<<endl,0;
        else if(times[b]==0)
            times[b]=2;
        else if(times[b]==2)//如果可以2次完成题目要求,并不代表后面没有更优秀的解. 
            ans=2;
    }
    cout<<ans<<endl;
    return 0;
} 

C Photo of The Sky

翻译

给你(2N)个数字,你可以任意排列，让你排成(N)个坐标，问你包含这(N)个坐标的矩形大小的最小值。

思路

明确了求的是最小值！找到一个面积最小长方形使得全部点都包含。

本题的精华可以说是：极差。

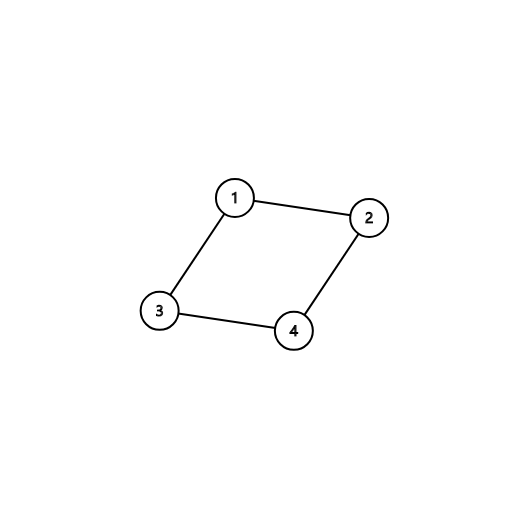
然后我们看一下上面的图片，既然都包含，那么满足啥？我们先讨论最大值和最小值包含在

• 我们就让点一与点二是全部能构成点中的极差最大的点（要是有比他大的你怎么包含）？

• 然后，我们确定了长，不过宽不必为极差最。那么我下面讲一下为啥。

因为我们只要将输入的数排个序，以(N)为界，左边为横坐标，右边为纵坐标。这样我们只要随便找2个点（位于(N)的两侧)，然后只要把比宽长的数作为横坐标，短或等于的作为纵坐标就可以啦（因为你的纵坐标在(N)的右边，对了别忘了你排顺序了哦）！

还有一种情况,那就是:最大值会在长里，最小值会在宽里，这样我们需要让最大值尽可能的小，最小值尽可能的大，由于排序，不就是(Easy)了吗？

于是我们可以总结出做法：先找一个基准数作为最小值（基准数为第二个情况的结果），然后确定长为最大值，枚举宽，更新答案。

一定要开long long！

用到了一些数学知识，我也不会，好不容易搞懂的，看不懂也没关系。

Code

#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
long long n,a[1000001];
int main()
{
    cin>>n;n*=2;
    for (int i=1; i<=n; i++)
        cin>>a[i];
    sort(a+1,a+n+1);
    long long ans=(a[n/2]-a[1])*(a[n]-a[n/2+1]);//先找到一个基准数，也是第二个情况的结果
    for (int i=2; i<=n/2+1; i++)//枚举并更新答案
        ans=min(ans,(a[i+n/2-1]-a[i])*(a[n]-a[1]));
    cout<<ans;
}

D Chemical table

翻译

给你一个图，这个图里面会有一些长方形与正方形，只要他们的四角中的任意三个角有一个(X)的话（请饶恕我这么形容），那么他就会在空缺的角形成一个新的(X)，你可以变出来一个(X)，给你这个图的大小以及哪里有(X)，问你至少要变出几个(X)才可以使得全图都是(X)。

思路

不亏是明星团队出的题，代码量不大但是思维坑啊。那么我就不绕了，直接入正题（听说有人五分钟切了这道题？）

这道题熟练图论的人可能会想到办法，按照套路，我们可以把有(X)的格子他们的行和列看为两个点，然后把全图跑一边，这样会形成一个图，那么这个图会长啥样？

我们先弄一下(2*2)的，假设他三个角都有了(X)。那么可能是下面这一种。

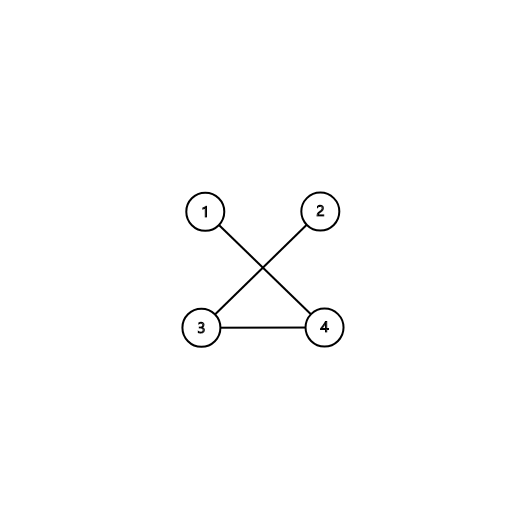
感觉到了什么，没错，这个图是联通的啊！只要有三个边四个点（四个点是格子的四角）一定是联通的！而且加不加第四个已经无所谓了？是不是？我们再以(2*2)为例子，看看只有两个边的情况。

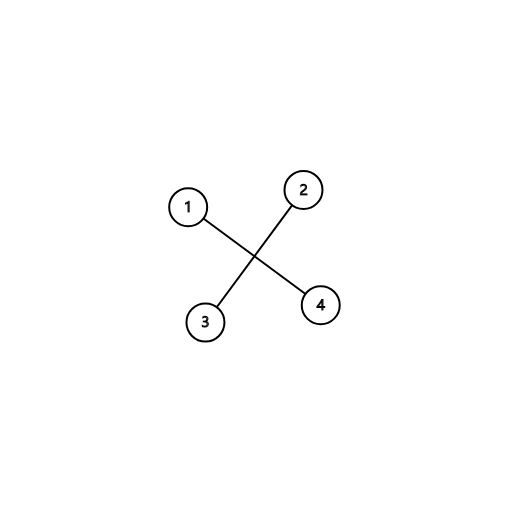
你可以容易的想到无论只有两个边或一个边或没有（一个边是一个(X)哦！），都不是联通的，这个时候，我们就想帮他联通。建一条边的话要变一次(X)，一直到整个图联通为止。就像，上图，每个加一个(X)就好了，因此答案是(1)

我们再上一下样例的图（上面是行，下面是列）：

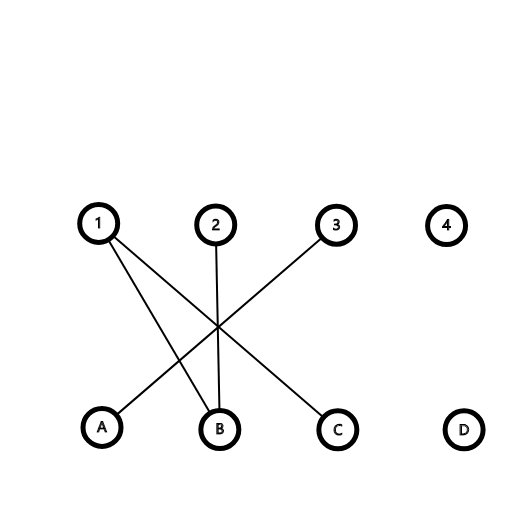
答案是(1)，你就会想，这不是要加两条边吗？？

这就怪了？？但是你仔细一想啊，上面两个图的联通块个数都是二，答案都是一！没错是联通块的个数再减一！！！

至此，我很啰嗦的啰嗦完了这道看上去啰嗦但是思想好代码不啰嗦的啰嗦题目,下面是超短代码，我竟然会给注释。

Code

#include<bits/stdc++.h> 
using namespace std;
int n,m,q; 
bool vis[500010];
vector<int>e[500010];

void dfs(int u)//最简单的求联通分量 
{
    vis[u]=1;
    int sz=e[u].size();
    for(int i=0;i<sz;i++)
        if(!vis[e[u][i]]) 
            dfs(e[u][i]);
}

int x, y,ans;
int main ()
{
    cin>>n>>m>>q;
    while(q--)
        cin>>x>>y, e[x].push_back(y+n), e[y+n].push_back(x);//为了好搜，于是行正常，列要加上X的个数 
    for(int i=1;i<=n+m;i++)
        if(!vis[i]) ans++, dfs(i);//统计答案 
    cout<<ans-1<<endl;
    return 0;
}