蓄水池采样问题

Posted 2021-01-04 wmx24

问题描述

 

要求从N个元素中随机的抽取k个元素，其中N无法确定。例如：

1. 从 100000 份调查报告中抽取 1000 份进行统计。
2. 从一本很厚的电话簿中抽取 1000 人进行姓氏统计。
3. 从 Google 搜索 "Ken Thompson"，从中抽取 100 个结果查看哪些是今年的。

这种应用的场景一般是数据流的情况下，由于数据只能被读取一次，而且数据量很大，并不能全部保存，因此数据量N是无法在抽样开始时确定的；但又要保持随机性，于是有了这个问题。

 

算法思想

 

假设数据序列的规模为 n，需要采样的数量的为 k。

首先构建一个可容纳 k 个元素的数组，将序列的前 k 个元素放入数组中。

然后从第 k+1 个元素开始，以 k/n 的概率来决定该元素是否被替换到数组中（数组中的元素被替换的概率是相同的）。 当遍历完所有元素之后，数组中剩下的元素即为所需采取的样本。

 

算法证明

 

对于第 i个数（i≤k）。在 k步之前，被选中的概率为 1。当走到第 k+1 步时，被 k+1个元素替换的概率 = k+1 个元素被选中的概率 * i 被选中替换的概率，即为 。则被保留的概率为 。依次类推，不被 k+2。则运行到第 n 步时，被保留的概率 = 被选中的概率 * 不被替换的概率，即： 个元素替换的概率为 

 

对于第 j 个数（j>k）。在第 j 步被选中的概率为 k/j。不被 j+1 个元素替换的概率为 。则运行到第 n 步时，被保留的概率 = 被选中的概率 * 不被替换的概率，即：

 

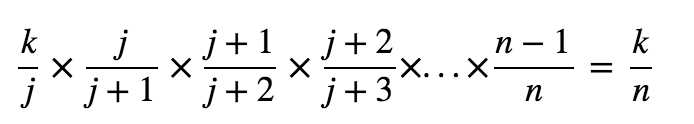
所以对于其中每个元素，被保留的概率都为 k/n. 蓄水池算法适用于对一个不清楚规模的数据集进行采样。