浅谈模拟频率，模拟角频率，数字角频率之间的关系

Posted 2021-01-04 dee-sir

模拟频率

模拟频率$f$表示“单位时间内完成周期性变化的次数”,是描述周期运动频繁程度的量。计量的单位是“次/秒”，为了纪念德国物理学家赫兹的贡献，人们把频率的单位命名为赫兹，简称“赫”，单位为 Hz。比如电脑显示器上面写的刷新率60Hz，就代表着显示器每秒刷新60次画面。

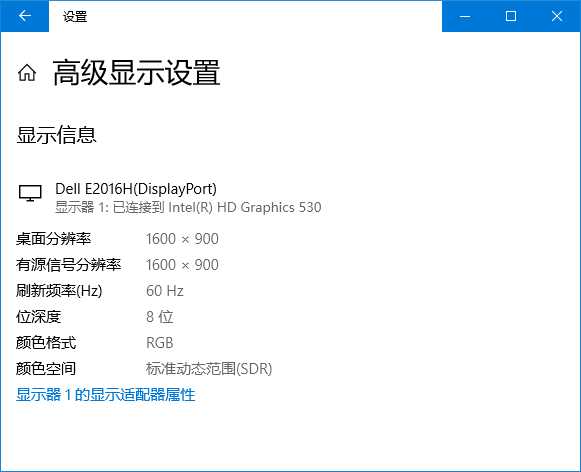
再比如我们常见的钟表，秒针每转一圈需要60s，所以周期$T=60s$,频率$f=frac{1}{T}=frac{1}{60}$. 秒针每转一圈，所转过的角度为$2pi$, 那么在单位时间内转过的角度为多少呢，这时候我们就需要引入角频率$omega$这个概念了。

模拟角频率

角频率$omega$同样是度量旋转快慢的物理量，含义是每秒转过多少弧度，单位是弧度每秒 $rad/s$。因为旋转一周的弧度是$2pi$, 要在单位时间内转过$f$圈，需要转过的角度就是$2pi imes f$即$$omega=frac{2pi}{T}=2pi f$$

 再举一个例子，比如$sin(t)$，它的图形如下，周期是$pi$，

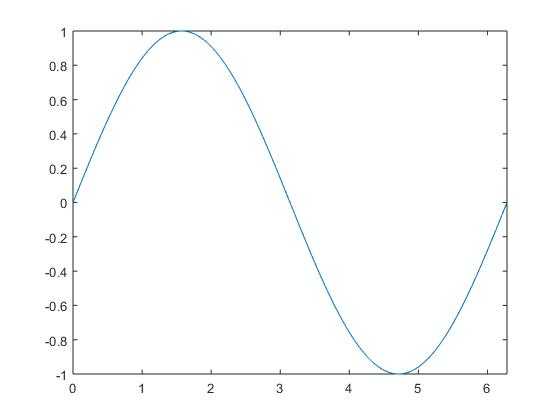
如果我们想在单位时间内完成$f$次周期，即模拟频率为$f$，则需要在单位时间内转过的角度为$2pi imes f$，所以模拟角频率为 $2pi f$，以$f=5$为例，其波形如图

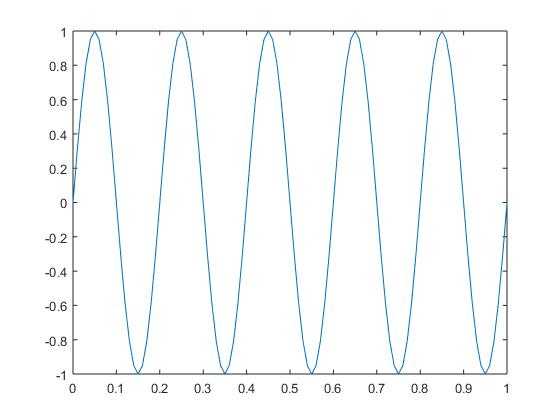
所用代码为：

t=0:0.01:1;
f=5;
w=2*pi*f;
y=sin(w*t);
plot(t,y);
xlim([0,1])

 

数字角频率

当我们用ADC采集信息时，是每隔$frac{1}{T_s}$产生一次采样，其中$T_s$是采样间隔，$T_s=frac{1}{Fs}$，比如我们用$Fs=50$对上述信号进行采样，那么两个相邻采样点的角度之差就是数字角频率$Omega$。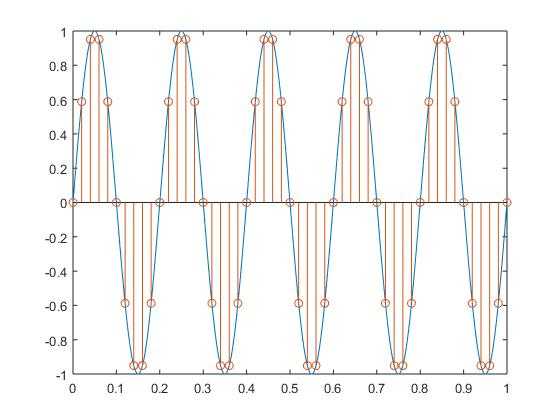

所用代码：

t=0:0.001:1;
f=5;
w=2*pi*f;
y=sin(w*t);
plot(t,y);
xlim([0,1])

hold on;
Fs=50;
t_s=0:1/Fs:1;
y_s=sin(w*t_s);
stem(t_s,y_s)

 

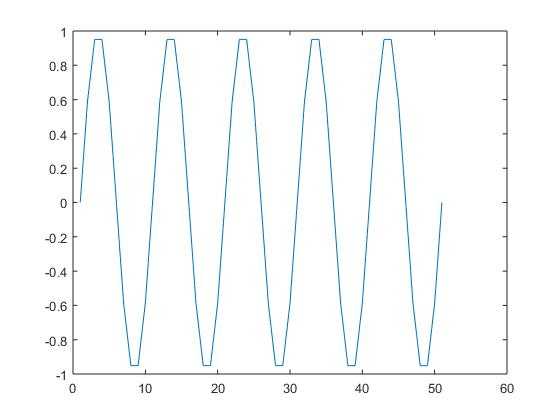
我们用离散点来重构一下

t=0:0.001:1;
f=5;
w=2*pi*f;
y=sin(w*t);
plot(t,y);
xlim([0,1])

hold on;
Fs=50;
t_s=0:1/Fs:1;
y_s=sin(w*t_s);
stem(t_s,y_s)

figure();
k=0:(size(t_s,2)-1);
OMEGA=2*pi*f/Fs;
y_k=sin(OMEGA*k);
plot(y_k);