第18课——队列的优化实现

Posted liu-jing

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第18课——队列的优化实现相关的知识，希望对你有一定的参考价值。

之前实现的顺序栈和链式栈的进栈和出栈操作时间复杂度都是O(1)。而用同样的方式实现队列，进队和出队的复杂度总有一个是O(n) 。
顺序队列的瓶颈

顺序队列

线性表的第一个元素作为队头

线性表的最后一个元素作为队尾

入队的新元素是在线性表的最后，时间复杂度为O(1)；

出队时需要将后续的所有元素向前移动，时间复杂度为O(n)；

技术分享图片

顺序队列的优化方案

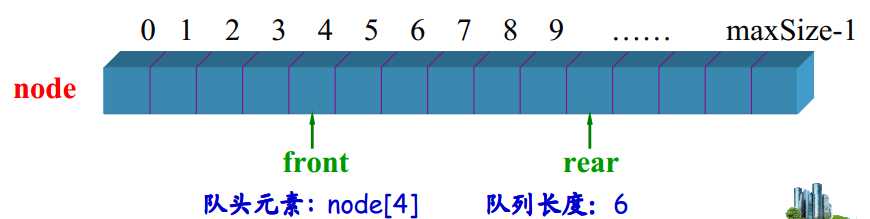
技术分享图片

技术分享图片

技术分享图片

定义顺序队列的头：

typedef unsigned int TSeqQueueNode;

typedef struct _tag_SeqQueue
{
    int capacity;
    int length;
    int front;
    int rear;
    TSeqQueueNode* node;
} TSeqQueue;

顺序队列的创建

SeqQueue* SeqQueue_Create(int capacity) // O(1)
{
    TSeqQueue* ret = NULL;
    
    if( capacity >= 0 )
    {
        ret = (TSeqQueue*)malloc(sizeof(TSeqQueue) + sizeof(TSeqQueueNode) * capacity);
    }
    
    if( ret != NULL )
    {
        ret->capacity = capacity;
        ret->length = 0;
        ret->front = 0;
        ret->rear = 0;
        ret->node = (TSeqQueueNode*)(ret + 1);
    }    
    return ret;
}

入队列

int SeqQueue_Append(SeqQueue* queue, void* item) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    int ret = (sQueue != NULL) && (item != NULL);
    
    ret = ret && (sQueue->length + 1 <= sQueue->capacity);
    
    if( ret )
    {
        sQueue->node[sQueue->rear] = (TSeqQueueNode)item;
        
        sQueue->rear = (sQueue->rear + 1) % sQueue->capacity;
        
        sQueue->length++;
    }    
    return ret;
}

出队列

void* SeqQueue_Retrieve(SeqQueue* queue) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    void* ret = SeqQueue_Header(queue);
    
    if( ret != NULL )
    {
        sQueue->front = (sQueue->front + 1) % sQueue->capacity;
        
        sQueue->length--;
    }
    
    return ret;
}

void* SeqQueue_Header(SeqQueue* queue) // O(1) 
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    void* ret = NULL;
    
    if( (sQueue != NULL) && (sQueue->length > 0) )
    {
        ret = (void*)(sQueue->node[sQueue->front]);
    }
    
    return ret;
}

出队列由原来的O(n)变成的O(1)；

完整版seqQueue.c代码：

技术分享图片 
#include <stdio.h>
#include <malloc.h>
#include "SeqQueue.h"

typedef unsigned int TSeqQueueNode;

typedef struct _tag_SeqQueue
{
    int capacity;
    int length;
    int front;
    int rear;
    TSeqQueueNode* node;
} TSeqQueue;

SeqQueue* SeqQueue_Create(int capacity) // O(1)
{
    TSeqQueue* ret = NULL;
    
    if( capacity >= 0 )
    {
        ret = (TSeqQueue*)malloc(sizeof(TSeqQueue) + sizeof(TSeqQueueNode) * capacity);
    }
    
    if( ret != NULL )
    {
        ret->capacity = capacity;
        ret->length = 0;
        ret->front = 0;
        ret->rear = 0;
        ret->node = (TSeqQueueNode*)(ret + 1);
    }
    
    return ret;
}

void SeqQueue_Destroy(SeqQueue* queue) // O(1)
{
    free(queue);
}

void SeqQueue_Clear(SeqQueue* queue) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    
    if( sQueue != NULL )
    {
        sQueue->length = 0;
        sQueue->front = 0;
        sQueue->rear = 0;
    }
}

int SeqQueue_Append(SeqQueue* queue, void* item) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    int ret = (sQueue != NULL) && (item != NULL);
    
    ret = ret && (sQueue->length + 1 <= sQueue->capacity);
    
    if( ret )
    {
        sQueue->node[sQueue->rear] = (TSeqQueueNode)item;
        
        sQueue->rear = (sQueue->rear + 1) % sQueue->capacity;
        
        sQueue->length++;
    }
    
    return ret;
}

void* SeqQueue_Retrieve(SeqQueue* queue) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    void* ret = SeqQueue_Header(queue);
    
    if( ret != NULL )
    {
        sQueue->front = (sQueue->front + 1) % sQueue->capacity;
        
        sQueue->length--;
    }
    
    return ret;
}

void* SeqQueue_Header(SeqQueue* queue) // O(1) 
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    void* ret = NULL;
    
    if( (sQueue != NULL) && (sQueue->length > 0) )
    {
        ret = (void*)(sQueue->node[sQueue->front]);
    }
    
    return ret;
}

int SeqQueue_Length(SeqQueue* queue) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    int ret = -1;
    
    if( sQueue != NULL )
    {
        ret = sQueue->length;
    }
    
    return ret;
}

int SeqQueue_Capacity(SeqQueue* queue) // O(1)
{
    TSeqQueue* sQueue = (TSeqQueue*)queue;
    int ret = -1;
    
    if( sQueue != NULL )
    {
        ret = sQueue->capacity;
    }
    
    return ret;
}
SeqQueue.c

main.c

#include <stdio.h>
#include <stdlib.h>
#include "SeqQueue.h"

/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int main(int argc, char *argv[]) 
{
    SeqQueue* queue = SeqQueue_Create(6);
    int a[10] = {0};
    int i = 0;
    
    for(i=0; i<10; i++)
    {
        a[i] = i + 1;
        
        SeqQueue_Append(queue, a + i);
    }
    
    printf("Header: %d
", *(int*)SeqQueue_Header(queue));
    printf("Length: %d
", SeqQueue_Length(queue));
    printf("Capacity: %d
", SeqQueue_Capacity(queue));
    
    while( SeqQueue_Length(queue) > 0 )
    {
        printf("Retrieve: %d
", *(int*)SeqQueue_Retrieve(queue));
    }
    
    printf("
");
    
    for(i=0; i<10; i++)
    {
        a[i] = i + 1;
        
        SeqQueue_Append(queue, a + i);

        printf("Retrieve: %d
", *(int*)SeqQueue_Retrieve(queue));
    }
    
    SeqQueue_Destroy(queue);
    
    return 0;
}

运行结果为：

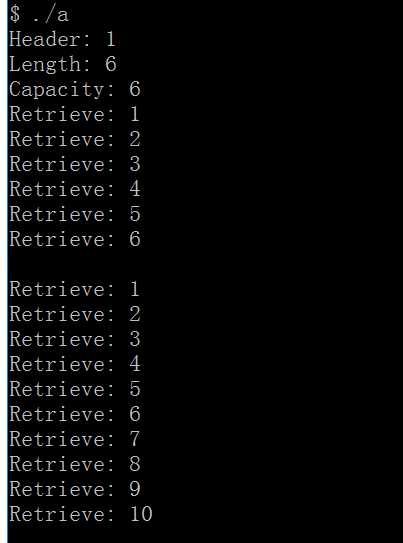
技术分享图片

同样的，我们来实现链式队列；

链式队列的头：

typedef struct _tag_LinkQueue
{
    TLinkQueueNode* front;
    TLinkQueueNode* rear;
    int length;
} TLinkQueue;

节点：

struct _tag_LinkQueueNode
{
    TLinkQueueNode* next;
    void* item;
};

创建：

LinkQueue* LinkQueue_Create() // O(1)
{
    TLinkQueue* ret = (TLinkQueue*)malloc(sizeof(TLinkQueue));
    
    if( ret != NULL )
    {
        ret->front = NULL;
        ret->rear = NULL;
        ret->length = 0;
    }
    
    return ret;
}

入队列：

int LinkQueue_Append(LinkQueue* queue, void* item) // O(1)
{
    TLinkQueue* sQueue = (TLinkQueue*)queue;
    TLinkQueueNode* node = (TLinkQueueNode*)malloc(sizeof(TLinkQueueNode));
    int ret = (sQueue != NULL ) && (item != NULL) && (node != NULL);
    
    if( ret )
    {
        node->item = item;
        
        if( sQueue->length > 0 )
        {
            sQueue->rear->next = node;
            sQueue->rear = node;
            node->next = NULL;
        }
        else
        {
            sQueue->front = node;
            sQueue->rear = node;
            node->next = NULL;
        }        
        sQueue->length++;
    }
    
    if( !ret )
    {
        free(node);
    }    
    return ret;
}

出队列：

void* LinkQueue_Retrieve(LinkQueue* queue) // O(1)
{
    TLinkQueue* sQueue = (TLinkQueue*)queue;
    TLinkQueueNode* node = NULL;
    void* ret = NULL;
    
    if( (sQueue != NULL) && (sQueue->length > 0) )
    {
        node = sQueue->front;
        
        sQueue->front = node->next;
        
        ret = node->item;
        
        free(node);
        
        sQueue->length--;
        
        if( sQueue->length == 0 )
        {
            sQueue->front = NULL;
            sQueue->rear = NULL;
        }
    }
    
    return ret;
}

main.c

#include <stdio.h>
#include <stdlib.h>
#include "LinkQueue.h"

/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int main(int argc, char *argv[]) 
{
    LinkQueue* queue = LinkQueue_Create();
    int a[10] = {0};
    int i = 0;
    
    for(i=0; i<10; i++)
    {
        a[i] = i + 1;
        
        LinkQueue_Append(queue, a + i);
    }
    
    printf("Header: %d
", *(int*)LinkQueue_Header(queue));
    printf("Length: %d
", LinkQueue_Length(queue));
    
   // LinkQueue_Clear(queue);
    
    while( LinkQueue_Length(queue) > 0 )
    {
        printf("Retrieve: %d
", *(int*)LinkQueue_Retrieve(queue));
    }
    
    LinkQueue_Destroy(queue);
    
    return 0;
}

运行结果：

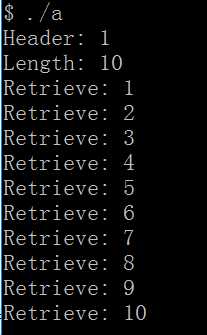
技术分享图片

优化后的队列，增加了front，rear后，入队和出队都是O(1)；

 


以上是关于第18课——队列的优化实现的主要内容，如果未能解决你的问题，请参考以下文章

第28章 算法优化体验课 - 骑士周游问题

perl中的队列

Selenium第18课 Jenkins

软件工程课设迭代开发第五天

# Java 常用代码片段

# Java 常用代码片段