XJOI2018提高组训训练23

Posted 2021-01-03 lmjer

估计得分：100+100+100+100+0+80+0=480

实际得分：100+100+100+100+0+90+20=510

T1 花痴

题目描述：Hongyan没事就在神秘岛上闲逛，岛上各种奇花异草数不胜数，钟情于花的他很快便被苹果树下的一丛奇花迷住了（路边的野花不要采哦！），他惊奇地发现，这些花的形状都是正多边形的，而且花瓣与花瓣之间的层层嵌套看起来就像将正多边形的每一对顶点都用线段连上了心的。酷爱数学的他居然想要将花朵上的每一对平行线都数出来……就像数星星似的，数来数去都数不完。远处，Worm已经做好饭准备叫大家吃了，为了不使hongyan挨饿，请你尽快帮帮他吧！

 

输入格式：

只有一个数N，4<=N<=2500

 

输出格式：

只有一个数,输出正N边形所有顶点对间连线中共有多少对平行线。

 

样例输入：

6

 

样例输出：

12

 

数据范围：

4<=N<=2500

估计得分：100

实际得分：100

分析：首先这道题十分有意思，我们会发现，一个正多边形，他的每一条对角线都可以找到至少一条边与他平行，所以得出多边形对角线数为n(n-3)/2

当变数为偶数时，因为两条对边还会平行，所以平行线的条数为n(n-3)/2+n/2化简得n（n-2)/2

当边数为奇数的时候我们发现

正七边形

 

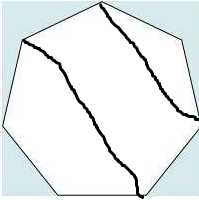
 我们会发现两条平行线，有两条平行线但是有三组平行线

当九边形

 

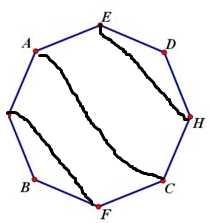
 我们会发现3条平行线，有两条平行线但是有6组平行线

所以n（n-3)/2条平行线，就有(n(n-3)/2)*(n-1)/4组

边为偶数的也一样

所以得出公式，代码见

代码：

 

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

int main(){
    long long n;
    long long total=0;
    scanf("%lld",&n);
    if(n%2) total=n*(n-3)*(n-1)/8;
    else total = n*(n-2)*(n-2)/8;
    printf("%lld
", total);
return 0;
}