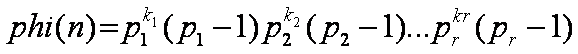9.1总结前日(数学+图论)
Posted romalzhih
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了9.1总结前日(数学+图论)相关的知识,希望对你有一定的参考价值。
后天就要开学了,这应该是这个暑假的最后一次总结了吧。
说实话,忙忙碌碌的一个暑假,学到东西了么?学到了。学了多少?还可以吧hhh。
想起来去年的这个时候,我还抱着紫书在那里看爆搜,啥也看不懂,现在呢,怎么说也懂得了一些吧。
路就是这样,你敢走,就有的走。
狭路相逢,勇者胜。
UVA 1645
题意:给出一个数n,求n个结点的树有多少种结构满足每个结点的子结点数相同。
解法:n结点树,除去根结点,有n-1个结点,根结点的每棵子树需要完全相同, 所以根结点的子树个数k,它们满足(n-1)%k==0。然后就可以递推打表了。
1 #include<cstdio> 2 using namespace std; 3 const int maxn = 1000 + 5; 4 const int mod = 1e9 + 7; 5 int f[maxn]; 6 void generate() { 7 f[0] = 0, f[1] = 1; 8 for (int i = 1; i < maxn; i++) 9 for (int k = 1; k < i; k++) {//枚举孩子节点数 10 if ((i - 1) % k)continue;//代表这种结点数的分配可以,故跳过 11 else f[i] = (f[i] + f[k]) % mod;//累加前一种分配方案 12 } 13 return; 14 } 15 int main() { 16 generate(); 17 int n, kase = 0; 18 while (scanf("%d", &n) != EOF) { 19 printf("Case %d: %d ", ++kase, f[n]); 20 } 21 return 0; 22 }
UVA557
题意:
Ben和Bill是一对双胞胎,生日那天他们请了2n个朋友(包括他们自己,题目给出的即为2n),然后有n个汉堡和n个三明治,然后由Ben的左边开始分食物,每个人选取食物的方式是先丢硬币,正面汉堡,反面是三明治,问最后双胞胎兄弟那道同一种食物的概率
解法:
概率论题目。
首先,吃到不同蛋糕的概率是C(i-1,2i-2)*0.5^(2i-2);这里的i最大值是一块蛋糕的数量。
然后,由这个式子可以得到一个递推式:p[i+1]/p[i]=(2i-1)/2i,之后递推打表即可
1 #include<cstdio> 2 using namespace std; 3 double p[100000 + 5]; 4 void generate() { 5 p[1] = 1.0, p[2] = 0.5, p[3] = 0.375; 6 for (int i = 3; i <= 100002; i++) 7 p[i+1] = p[i] * ( 1.0*2 * i - 1) / ( 1.0*2 * i); 8 return; 9 } 10 int main() { 11 generate(); 12 int T; scanf("%d", &T); 13 while (T--) { 14 int n; scanf("%d", &n); 15 printf("%.4f ", 1 - p[n / 2]); 16 } 17 return 0; 18 }
UVA11526
题意:计算 sum{ n/i }=? (1<=i<=n)(n<=2147483647)
解法:
首先打表之后发现规律,对于除数相同的项数超过或等于两项的i,都有规律s(i)=n/i-n/(i+1)。
由此我们先从小到大计算这些项,但是这个级数的增长到后来就不是自然数增长了,所以当s(i)=1的以后, 我们就跳出这个循环,开始遵循样例中的做法进行计算。
注意刚开始枚举的是商,之后枚举的是除数;其次还应注意n<0时的情况处理,直接输出0即可。
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 typedef long long ll; 5 int main() { 6 int T; scanf("%d", &T); 7 while (T--) { 8 ll n; scanf("%lld", &n); 9 ll i = 0, ans = 0; 10 do { 11 ans += (++i)*(n / i - n / (i + 1)); 12 } while (n / i - n / (i + 1) > 1 && i <= n); 13 i = n / (i + 1); 14 while (i >= 1)ans += n / i--; 15 printf("%lld ", n <= 0 ? 0 : ans); 16 } 17 return 0; 18 }
UVA12063
题意:
问有多少个N(N<=64)位二进制数满足这样的要求:
(1)没有前导0
(2)0的数目和1的数目相等
(3)可以被K(K<=100)整除
解法:
本题利用数位dp解决。即通过寻找数位上的递推式来加以解决。从样例可知,如果只是一个个的枚举,时间上肯定是承受不了的,必须通过寻找递推式来加以解决。通过观察,我们发现,如果一个整数n能够被k整除,即n%k==0,假如这个数的二进制形如1XXX这样的二进制,也就意味着二进制数1000的值模k的余数和二进制数XXX的值模k的余数之和正好为0。这样的话我们设d(cur,m,MOD)来表示cur位二进制数中有m个1,且它们的值模k均为MOD的数的个数。那么本题的最终答案就是d(n-1,(n-1)/2,(k-mid[n])),因为第n位有一个1,前n-1位只需要(n-1)/2个1即可。
那么问题转化为如何快速求解d(cur,m,MOD)。分两种情况:(1)如果第cur为填写0,那么结果是d(cur-1,m,MOD)。(2)如果第cur位填写1,那么结果是d(cur-1,m-1,(MOD-mod[cur]))(mod[cur]表示长度为cur,第一位为1,后面均为0的二进制数模k的结果。程序中为了防止余数变为负数,多了一个加k后模k的部分)。根据加法原理即得到下列递推式:
d(cur,m,MOD)=d(cur-1,m,MOD)+d(cur-1,m-1,MOD-mod[cur])(cur>0)
那么当cur==0时到达了递归边界,此时的MOD应该满足MOD%k==0,返回1,否则返回0。
本题的数位dp的设置方式值得我们学习。
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 typedef long long ll; 5 const int maxn = 70; 6 const int maxk = 100; 7 ll d[maxn + 10][maxn * 2 + 10][maxk + 10], mod[maxn + 10]; 8 ll n, k; 9 10 //事先计算二进制数1000...模k的余数 11 void generate() { 12 mod[1] = 1; 13 for (int i = 2; i <= maxn; i++) 14 mod[i] = (mod[i - 1] << 1) % k; 15 return; 16 } 17 18 ll dp(int cur,int O,int MOD) {//前cur位,有O个1,这些数的余数均为MOD的数的个数 19 if (cur == 0) { 20 if (O) return 0; 21 //cur为0的时候,MOD模k的余数应当为0,如果是,返回1,否则返回0 22 return d[cur][O][MOD] = ((MOD%k == 0) ? 1 : 0); 23 } 24 if (d[cur][O][MOD] != -1)return d[cur][O][MOD]; 25 ll &ans = d[cur][O][MOD]; 26 ans = dp(cur - 1, O, MOD);//第cur位填写零的个数 27 //第cur位填写1的个数,那么前cur-1位有O-1个1 28 if (O > 0)ans += dp(cur - 1, O - 1, (MOD - mod[cur] + k) % k); 29 return ans; 30 } 31 32 int main() { 33 int T; cin >> T; 34 int kase = 1; 35 while (T--) { 36 memset(d, -1, sizeof(d)); 37 cin >> n >> k; 38 if (k == 0 || (n & 1)) { 39 cout << "Case " << kase++ << ": " << 0 << endl; 40 continue; 41 } 42 generate(); 43 //最终的结果是前n-1位(最低位为1),且余数为k-mod[n]的二进制数的个数, 44 //因为这样的数与n位二进制数(1000...)的余数mod[n]相加恰好为0 45 ll ans = dp(n - 1, (n - 1) / 2, (k - mod[n]) % k); 46 cout << "Case " << kase++ << ": " << ans << endl; 47 } 48 return 0; 49 }
UVA10837
题意:
给你一个欧拉函数值 phi(n),问最小的n是多少。 phi(n) <= 100000000 , n <= 200000000
解法:
这里的k有可能是等于0的,所以不能直接将phi(n)分解质因子。但是可以知道(Pr - 1)是一定存在的,那就直接枚举素数,满足phi(n) % (Pr-1)的都加进去,然后对这些素数进行爆搜。。。说到底还是暴力啊。。。想不到什么巧妙的办法了,最后需要注意的是,一遍枚举完各个素数后phi(n)除后还剩now,现在要判断(now+1)是否为素数,还是保证这个素数前面没有访问过。
因为幂可以为0,所以不能直接质因数分解,要枚举枚举p1-1
计算的过程中phi(n)第一次除以(pr-1),答案就乘以pr,后来 phi(n)每次都是除以pr
答案乘以pr。因为n = p1^k1 * p2^k2……pr^kr,而phi(n) = p1^(k1-1) * (p1-1) * p2^(k2-1) * (p2-1)……pr^(kr-1) * (pr-1)
1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstring> 5 #include<vector> 6 #define REP(i, a, b) for(int i = (a); i < (b); i++) 7 #define REP_DOWN(i, a, b) for(int i=(a); i< (n); i--) 8 using namespace std; 9 const int maxn = 10000 + 10; 10 bool is_prime[maxn], vis[maxn]; 11 vector<int>prime, g; 12 int ans; 13 14 void get_prime(){ 15 memset(is_prime, true, sizeof(is_prime)); 16 is_prime[0] = is_prime[1] = false; 17 REP(i, 2, maxn) 18 { 19 if (is_prime[i]) prime.push_back(i); 20 REP(j, 0, prime.size()) 21 { 22 if (i * prime[j] > maxn) break; 23 is_prime[i * prime[j]] = false; 24 if (i % prime[j] == 0) break; 25 } 26 } 27 return; 28 } 29 30 void split(int n) { 31 ans = 2e9; 32 g.clear(); 33 REP(i, 0, prime.size())if (n % (prime[i] - 1) == 0) 34 g.push_back(prime[i]); 35 } 36 37 bool check(int sum) { 38 REP(i, 0, prime.size()) { 39 if (prime[i] * prime[i] > sum)break; 40 if (sum%prime[i] == 0)return false; 41 } 42 REP(i, 0, prime.size()) 43 if (vis[i] && prime[i] == sum) 44 return false; 45 return true; 46 } 47 48 void dfs(int p,int sum,int tot) { 49 if (p == prime.size()) { 50 if (sum == 1)ans = min(ans, tot); 51 else if (check(sum + 1)) 52 ans = min(ans, tot*(sum + 1)); 53 return; 54 } 55 56 dfs(p + 1, sum, tot); 57 if (sum % (prime[p] - 1))return; 58 vis[p] = 1; 59 sum /= prime[p] - 1; 60 tot *= prime[p]; 61 dfs(p + 1, sum, tot); 62 63 while (sum%prime[p] == 0) { 64 sum /= prime[p]; 65 tot *= prime[p]; 66 dfs(p + 1, sum, tot); 67 } 68 vis[p] = 0; 69 } 70 71 int main() { 72 get_prime(); 73 int n, kase = 0; 74 while (scanf("%d", &n) && n) { 75 split(n); 76 memset(vis, 0, sizeof(vis)); 77 dfs(0, n, 1); 78 printf("Case %d: %d %d ", ++kase, n, ans); 79 } 80 return 0; 81 }
UVA 12219
题意:给定一个字符串,根据字符串建树,然后可以把树化简成一个图,最后根据图输出一行字符串
解法:对左右子树进行一个编码之后的再分配,map快速查询
1 #include<cstdio> 2 #include<string> 3 #include<map> 4 using namespace std; 5 #define REP(i, a, b) for(int i = (a); i < (b); i++) 6 #define REP_DOWN(i, a, b) for(int i=(a); i< (n); i--) 7 8 const int maxn = 60000 + 10; 9 int rnd, cnt, done[maxn]; 10 char expr[maxn * 5], *p; 11 struct Node { 12 string s; 13 int hash, left, right; 14 Node() :s(""), hash(0), left(-1), right(-1) {} 15 bool operator < (const Node &rhs)const { 16 if (hash != rhs.hash)return hash < rhs.hash; 17 else if (left != rhs.left)return left < rhs.left; 18 else return right < rhs.right; 19 } 20 }node[maxn]; 21 map<Node, int>dict; 22 23 int solve() { 24 int id = cnt++; 25 Node &u = node[id]; 26 u.hash = 0, u.left = -1, u.right = -1, u.s = "";//直接调用一次构函不行,多组样例 27 while (isalpha(*p)) {//由于是由1~4个字母的组成的,所以这里需要进行一个递推 28 u.hash = u.hash * 27 + *p - ‘a‘ + 1; 29 u.s.push_back(*p);//提取字符 30 p++; 31 } 32 if (*p == ‘(‘) { 33 p++;//跳过这个括号 34 u.left = solve(), p++; 35 u.right = solve(), p++; 36 } 37 if (dict.count(u)) {//这棵树的代码已经有了,代表这棵树已经出现过了,就将它原来的编号复制就行 38 cnt--; 39 return dict[u]; 40 } 41 return dict[u] = id; 42 } 43 44 void print(int v) { 45 if (done[v] == rnd)printf("%d", v + 1); 46 else { 47 done[v] = rnd; 48 printf("%s", node[v].s.c_str());//printf输出string 49 if (node[v].left != -1) { 50 putchar(‘(‘); 51 print(node[v].left); 52 putchar(‘,‘); 53 print(node[v].right); 54 putchar(‘)‘); 55 } 56 } 57 return; 58 } 59 60 int main() { 61 int T; scanf("%d", &T); 62 while (T--) { 63 rnd++, cnt = 0, dict.clear(); 64 scanf("%s", expr); 65 p = expr;//扫描指针 66 print(solve()); 67 putchar(10);//换行符 68 } 69 return 0; 70 }
UVA1395
题意:
给你一个图,求一个生成树,使其苗条度最小
苗条度:生成树的最大边减去最小边的值。
解法:
生成树的思想运用。
首先将所有的边按边权值从小到大排序后,枚举左起点L,从L依次遍历右起点R,如果L~R使得图形成了一个生成树, 那么一定存在最小的W[R]-W[L],否则就是-1
1 #include<cstdio> 2 #include<algorithm> 3 #define REP(i, a, b) for(int i = (a); i < (b); i++) 4 #define REP_DOWN(i, a, b) for(int i=(a); i< (n); i--) 5 using namespace std; 6 const int INF = 0x3fffffff; 7 struct edge { int u, v, w; }g[10000 + 5]; 8 bool cmp(edge a, edge b) { return a.w < b.w; } 9 10 int p[110]; 11 int findSet(int x) { return p[x] == x ? x : p[x] = findSet(p[x]); } 12 13 int main() { 14 int n, m; 15 while (scanf("%d%d", &n, &m) && n) { 16 REP(i, 0, m) scanf("%d%d%d", &g[i].u, &g[i].v, &g[i].w); 17 18 sort(g, g + m, cmp); 19 int ans = INF; 20 REP(L, 0, m) { 21 REP(i, 1, n + 1) p[i] = i; 22 int cnt = n; 23 REP(R, L, m) { 24 int u = g[R].u, v = g[R].v; 25 int x = findSet(u), y = findSet(v); 26 if (x != y) { 27 p[x] = y; 28 if (--cnt == 1) { ans = min(ans, g[R].w - g[L].w); break; } 29 } 30 } 31 } 32 33 printf("%d ", ans == INF ? -1: ans); 34 } 35 return 0; 36 }
UVA1151
题意:
平面上有n个点(1<=N<=1000),你的任务是让所有n个点连通,为此,你可以新建一些边,费用等于两个端点的欧几里得距离的平方。
另外还有q(0<=q<=8)个套餐,可以购买,如果你购买了第i个套餐,该套餐中的所有结点将变得相互连通,第i个套餐的花费为Ci。
求最小花费。
解法:
非常好的一道题。,写法也很有技巧
首先我们先把原来的点两两之间连一道边,然后跑一遍最小生成树,选出来我们要的边, 之后在此基础上我们枚举所有的方案数,取最小的那种即可。 这样做的原因是,因为在Kruskal算法中,两端已经属于同一连通分量的边不会进入最小生成树。 买了套餐之后,相当于一些边的权值变为了0,而对于不在套餐中的边e,排序在e前的边一个都没有少, 反而可能多了一些权值为0的边,所以在原图Kruskal扔掉的边,在后面的Kruskal一样会被扔掉。
除此之外,还应该学习的是如何利用二进制进行任意自己枚举,这个写法比较有代表性
1 #include<cstdio> 2 #include<algorithm> 3 #include<vector> 4 #define REP(i, a, b) for(int i = (a); i < (b); i++) 5 #define REP_DOWN(i, a, b) for(int i=(a); i< (b); i--) 6 using namespace std; 7 8 struct Edge { int u, v, w; }; 9 bool cmp(Edge a, Edge b) { return a.w < b.w; } 10 const int maxn = 1000 + 10; 11 int n, q; 12 int cost[maxn]; 13 int x[maxn], y[maxn]; 14 vector<int>sub[maxn]; 15 16 int p[maxn]; 17 int findSet(int x) { return p[x] == x ? x : p[x] = findSet(p[x]); } 18 19 int MST(int cnt, const vector<Edge>& e, vector<Edge>& o) { 20 //这里cnt代表着实际有多少个点,因为在枚举并缩点之后,原图的边数并不会变化,素以就需要一个量来控制 21 if (cnt == 1)return 0; 22 int ans = 0; o.clear(); 23 REP(i, 0, e.size()) { 24 int x = findSet(e[i].u), y = findSet(e[i].v); 25 if (x != y) { 26 //能被选入的量一定是没有缩点的量 27 p[x] = y; ans += e[i].w; 28 o.push_back(e[i]); 29 if (--cnt == 1)break; 30 } 31 } 32 return ans; 33 } 34 35 int main() { 36 int T; scanf("%d", &T); 37 while (T--) { 38 scanf("%d%d", &n, &q); 39 REP(i, 0, q) sub[i].clear(); 40 REP(i, 0, q) { 41 int cnt; scanf("%d%d", &cnt, &cost[i]); 42 REP(j, 0, cnt) { 43 int o; scanf("%d", &o); 44 sub[i].push_back(o - 1); 45 } 46 } 47 48 vector<Edge>e, o; 49 REP(i, 0, n) scanf("%d%d", &x[i], &y[i]); 50 REP(i, 0, n) REP(j, i + 1, n) { 51 int w = (x[i] - x[j])*(x[i] - x[j]) + (y[i] - y[j])*(y[i] - y[j]); 52 e.push_back({ i,j,w }); 53 } 54 55 REP(i, 0, n)p[i] = i; 56 sort(e.begin(), e.end(), cmp); 57 int ans = MST(n, e, o); 58 59 //二进制枚举子集 60 REP(mask, 0, (1 << q)) { 61 REP(i, 0, n) p[i] = i; 62 int cnt = n, c = 0; 63 REP(i, 0, q)if ((1 << i)&mask) { 64 c += cost[i]; 65 //缩点:两个点之间的权值为0,相当于将这两个点合并成一个点 66 REP(j, 1, sub[i].size()) { 67 int x = findSet(sub[i][j]), y = findSet(sub[i][0]); 68 if (x != y) { p[x] = y, cnt--; } 69 } 70 } 71 72 vector<Edge>useless; 73 ans = min(ans, MST(cnt, o, useless) + c); 74 } 75 76 printf("%d ", ans); 77 if (T)putchar(10); 78 } 79 return 0; 80 }
UVA247
题意:
如果两个人互相打电话(直接或者间接),则说他们在同一个电话圈里。例如,a打给b,b打给c,c打给d,d打给a,则这四个人在同一个圈里;如果e打给f,而f不打给e,则不能推出e和f在同一个电话圈。输入n(n<=25)个人的m次电话,找出所有的电话圈。人名只包含字母,不超过25个字符,且不重复。
解法:
有时候在一个图中我们并不关心两点之间的路径长度,我们只关心两点之间是否有通路, 这样,我们用1表示通路,0表示不通,求是否存在这样的通路的过程叫做:求有向图的传递闭包,Floyd算法可解
注意Floyd在使用之前需要初始化一次,其次还要加深dfs遍历联通快的学习
1 #include<iostream> 2 #include<cstring> 3 #include<string> 4 #include<map> 5 #include<set> 6 using namespace std; 7 #define INF 0x3f3f3f3f 8 #define REP(i, a, b) for(int i = (a); i < (b); i++) 9 #define MEM(a,x) memset(a,x,sizeof(a)) 10 11 map<string, int>mp; 12 map<int, string>rev_mp; 13 int g[30][30], vis[30]; 14 int n, m, kase = 0; 15 16 void dfs(int u) { 17 vis[u] = 1; 18 REP(i, 0, n) { 19 if (!vis[i] && g[u][i] && g[i][u]) { 20 cout << ", " << rev_mp[i]; 21 dfs(i); 22 } 23 } 24 return; 25 } 26 27 int main() { 28 while (cin >> n >> m&&n) { 29 mp.clear(); rev_mp.clear(); 30 MEM(g, 0); MEM(vis, 0); 31 32 int cnt = 0; 33 REP(i, 0, m) { 34 string x, y; cin >> x >> y; 35 if (mp.find(x) == mp.end())mp[x] = cnt, rev_mp[cnt++] = x; 36 if (mp.find(y) == mp.end())mp[y] = cnt, rev_mp[cnt++] = y; 37 g[mp[x]][mp[y]] = 1; 38 } 39 40 REP(i, 0, n) g[i][i] = 1; 41 REP(k, 0, n)REP(i, 0, n)REP(j, 0, n) 42 g[i][j] = g[i][j] || (g[i][k] && g[k][j]); 43 44 if (kase > 0) cout << endl; 45 cout << "Calling circles for data set " << ++kase <<":"<< endl; 46 REP(i, 0, n) { 47 if (!vis[i]) { 48 cout << rev_mp[i]; 49 dfs(i); 50 cout << endl; 51 } 52 } 53 } 54 return 0; 55 }
UVA10048
题意:从a点到b点, 找到一条路径,使得这条路径上的所有噪音中最大的值是所有路径中最小的, 这个噪音值便是要求的。
解法:希望路上经过的最大噪声值最小,就是Floyd中的加号变成max即可
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #define INF 0x3f3f3f3f 5 #define REP(i, a, b) for(int i = (a); i < (b); i++) 6 #define MEM(a,x) memset(a,x,sizeof(a)) 7 using namespace std; 8 int d[110][110]; 9 10 int main() { 11 int C, S, Q, kase = 0; 12 while (scanf("%d%d%d", &C, &S, &Q) && C) { 13 MEM(d, INF); 14 REP(i, 0, S) { 15 int u, v, w; 16 scanf("%d%d%d", &u, &v, &w); 17 u--, v--; 18 d[u][v] = d[v][u] = w; 19 } 20 21 REP(i, 0, C)d[i][i] = 0; 22 REP(k, 0, C)REP(i, 0, C)REP(j, 0, C) 23 d[i][j] = min(d[i][j], max(d[i][k], d[k][j])); 24 25 if (kase > 0) printf(" "); 26 printf("Case #%d ", ++kase); 27 28 REP(i, 0, Q) { 29 int u, v; 30 scanf("%d%d", &u, &v); 31 u--, v--; 32 if (d[u][v] == INF)printf("no path "); 33 else printf("%d ", d[u][v]); 34 } 35 } 36 return 0; 37 }
UVA753
题意:
题目的意思就是有n种插口,然后有m个设备,每个设备可以插一种插口,然后有k种(注意是种,个数不限)转换器,可以把一种设备的插口转成另一种.
现在问有几个设备充不上电.
解法:
首先用一个超级源点 把插口都连到超级源点,容量为1.
然后把所有设备都连到超级汇点.
然后通过转化器构造中间的边,容量是INF.
在ek模板算法就能算出最大流.
1 #include<iostream> 2 #include<string> 3 #include<queue> 4 #include<algorithm> 5 #include<vector> 6 #include<cstring> 7 #define INF 0x3f3f3f3f 8 #define REP(i, a, b) for(int i = (a); i < (b); i++) 9 #define MEM(a,x) memset(a,x,sizeof(a)) 10 #define MAXN 500+10 11 using namespace std; 12 13 vector<string>names; 14 int n, m, k; 15 int device[MAXN], target[MAXN];//电器,插座 16 int from[MAXN], to[MAXN];//转化器 17 18 //给所有没有序号的字符串进行编序号 19 int ID(string &s) { 20 REP(i, 0, names.size()) 21 if (names[i] == s)return i; 22 names.push_back(s); 23 return names.size() - 1; 24 } 25 26 struct Edge { 27 int from, to, cap, flow; 28 }; 29 struct Dinic { 30 int n, m, s, t; 31 vector<Edge>edges; 32 vector<int>G[MAXN]; 33 bool vis[MAXN]; 34 int d[MAXN]; 35 int cur[MAXN]; 36 37 void init(int n) { 38 for (int i = 0; i < n; i++) G[i].clear(); 39 edges.clear(); 40 } 41 42 void AddEdge(int from, int to, int cap) { 43 edges.push_back({ from, to, cap, 0 }); 44 edges.push_back({ to, from, 0, 0 }); 45 m = edges.size(); 46 G[from].push_back(m - 2); 47 G[to].push_back(m - 1); 48 } 49 bool BFS() { 50 int x, i; 51 memset(vis, 0, sizeof(vis)); 52 queue<int>Q; 53 Q.push(s); 54 d[s] = 0; 55 vis[s] = 1; 56 while (!Q.empty()) { 57 x = Q.front(), Q.pop(); 58 for (i = 0; i < G[x].size(); i++) { 59 Edge & e = edges[G[x][i]]; 60 if (!vis[e.to] && e.cap > e.flow) { 61 vis[e.to] = 1; 62 d[e.to] = d[x] + 1; 63 Q.push(e.to); 64 } 65 } 66 } 67 return vis[t]; 68 } 69 int DFS(int x, int a) { 70 if (x == t || a == 0) 71 return a; 72 int flow = 0, f; 73 for (int &i = cur[x]; i < G[x].size(); i++) { 74 Edge & e = edges[G[x][i]]; 75 if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) { 76 e.flow += f; 77 edges[G[x][i] ^ 1].flow -= f; 78 flow += f; 79 a -= f; 80 if (a == 0) 81 break; 82 } 83 } 84 return flow; 85 } 86 int Maxflow(int s, int t) { 87 this->s = s, this->t = t; 88 int flow = 0; 89 while (BFS()) { 90 memset(cur, 0, sizeof(cur)); 91 flow += DFS(s, INF); 92 } 93 return flow; 94 } 95 }; 96 Dinic g; 97 98 int main() { 99 int T; cin >> T; 100 while (T--) { 101 names.clear(); 102 cin >> n; 103 REP(i,0,n){ 104 string s; cin >> s; 105 target[i] = ID(s); 106 } 107 cin >> m; 108 REP(i, 0, m) { 109 string s1, s2; cin >> s1 >> s2; 110 device[i] = ID(s2); 111 } 112 cin >> k; 113 REP(i, 0, k) { 114 string s1, s2; cin >> s1 >> s2; 115 from[i] = ID(s1), to[i] = ID(s2); 116 } 117 118 int V = names.size(); 119 g.init(V + 2);//初始化的时候多了两个点,起点和汇点 120 REP(i, 0, m) g.AddEdge(V, device[i], 1);//给所有的电器连一条起点到它的边 121 REP(i, 0, n) g.AddEdge(target[i], V + 1, 1);//对所有的插座连一条它到终点的边 122 REP(i, 0, k) g.AddEdge(from[i], to[i], INF);//给所有的用电器连一条容量为无限的边 123 124 int r = g.Maxflow(V, V + 1);//其实有点最小割的感觉 125 cout << m - r << endl; 126 if (T)cout << endl; 127 } 128 return 0; 129 }
UVA1658
题意:
给出v(<=1000)个点和e(<=10000)条边的有向图,求1~v的两条不相交(除了起点终点外没有公共点)的路径,使得权和最小。
解法:
除了1和n的每个点我们进行拆点,点2~n-1拆成弧i->i‘,前者编号为0~n-1,后者编号为n~2n-3 之后我们跑一个固定流的最小费用即可
简称,拆点法
1 #include<cstdio> 2 #include<vector> 3 #include<cstring> 4 #include<queue> 5 #define INF 0x3f3f3f3f 6 #define REP(i, a, b) for(int i = (a); i < (b); i++) 7 #define MEM(a,x) memset(a,x,sizeof(a)) 8 #define MAXN 10000+10 9 using namespace std; 10 11 struct Edge { 12 int from, to, cap, flow, cost; 13 Edge(int u, int v, int c, int f, int w) :from(u), to(v), cap(c), flow(f), cost(w) {} 14 }; 15 16 struct MCF { 17 int n, m; 18 vector<Edge> edges; 19 vector<int> G[MAXN]; 20 int inq[MAXN]; // 是否在队列中 21 int d[MAXN]; // Bellman-Ford 22 int p[MAXN]; // 上一条弧 23 int a[MAXN]; // 可改进量 24 void init(int n) { 25 this->n = n; 26 for (int i = 0; i < n; i++) G[i].clear(); 27 edges.clear(); 28 } 29 void AddEdge(int from, int to, int cap, int cost) { 30 edges.push_back(Edge(from, to, cap, 0, cost)); 31 edges.push_back(Edge(to, from, 0, 0, -cost)); 32 m = edges.size(); 33 G[from].push_back(m - 2); 34 G[to].push_back(m - 1); 35 } 36 bool BellmanFord(int s, int t, int flow_limit, int& flow, int& cost) { 37 for (int i = 0; i < n; i++) d[i] = INF; 38 memset(inq, 0, sizeof(inq)); 39 d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF; 40 41 queue<int> Q; 42 Q.push(s); 43 while (!Q.empty()) { 44 int u = Q.front(); Q.pop(); 45 inq[u] = 0; 46 for (int i = 0; i < G[u].size(); i++) { 47 Edge& e = edges[G[u][i]]; 48 if (e.cap > e.flow && d[e.to] > d[u] + e.cost) { 49 d[e.to] = d[u] + e.cost; 50 p[e.to] = G[u][i]; 51 a[e.to] = min(a[u], e.cap - e.flow); 52 if (!inq[e.to]) { Q.push(e.to); inq[e.to] = 1; } 53 } 54 } 55 } 56 if (d[t] == INF) return false; 57 if (flow + a[t] > flow_limit) a[t] = flow_limit - flow; 58 flow += a[t]; 59 cost += d[t] * a[t]; 60 for (int u = t; u != s; u = edges[p[u]].from) { 61 edges[p[u]].flow += a[t]; 62 edges[p[u] ^ 1].flow -= a[t]; 63 } 64 return true; 65 } 66 // 最小费用流(流量确定) 67 // 需要保证初始网络中没有负权圈 68 int MincostFlow(int s, int t, int flow_limit, int& cost) { 69 int flow = 0; cost = 0; 70 while (flow < flow_limit && BellmanFord(s, t, flow_limit, flow, cost)); 71 return flow; 72 } 73 }g; 74 75 int main() { 76 int n, m; 77 while (scanf("%d%d", &n, &m) == 2 && n) { 78 g.init(2 * n - 2); 79 REP(i, 2, n) g.AddEdge(i - 1, i + n - 2, 1, 0); 80 REP(k, 0, m) { 81 int u, v, w; 82 scanf("%d%d%d", &u, &v, &w); 83 // 连u‘->v 84 if (u != 1 && u != n) u += n - 2; 85 else u--; 86 v--; 87 g.AddEdge(u, v, 1, w); 88 } 89 int cost; 90 g.MincostFlow(0, n - 1, 2, cost); 91 printf("%d ", cost); 92 } 93 return 0; 94 }
UVA1349
题意:给定一些有向带权边,求出把这些边构造成一个个环,总权值最小
解法:
对于带权的二分图的匹配问题可以用通过KM算法求解。
要求最大权匹配就是初始化g[i][j]为0,直接跑就可以;
要求最小权匹配就是初始化g[i][j]为-INF,加边的时候边权为负,最后输出答案的相反数。
因为要求每个点恰好属于一个圈,意味着每个点都有一个唯一的后继。 反过来,只要每个点都有唯一的后继,每个点一定属于某个圈。
唯一的是我们想到了二分图的概念,我们对于每个点,建立由u到v的二分图, 之后问题就转换成了二分图上的最小权完美匹配问题
1 #include<bits/stdc++.h> 2 #define REP(i, a, b) for(int i = (a); i < (b); i++) 3 #define MEM(a,x) memset(a,x,sizeof(a)) 4 #define INF 0x3f3f3f3f 5 #define MAXN 100+10 6 using namespace std; 7 8 struct KM { 9 int n; 10 int g[MAXN][MAXN]; 11 int Lx[MAXN], Ly[MAXN]; 12 int slack[MAXN];//记录距X匹配到Y点还需要多少权值 13 int match[MAXN];//记录每个X点匹配到的Y集中的点 14 bool S[MAXN], T[MAXN]; 15 16 void init(int n) { 17 this->n = n; 18 for (int i = 0; i < n; i++) 19 for (int j = 0; j < n; j++) 20 g[i][j] = -INF; 21 //注意这里如果是求最大权值匹配和就赋值为0 22 //最小权值匹配和就是—INF 23 } 24 25 void add_Edge(int u, int v, int val) { 26 g[u][v] = max(g[u][v], val); 27 } 28 29 bool dfs(int i) { 30 S[i] = true; 31 for (int j = 0; j < n; j++) { 32 if (T[j]) continue; 33 int tmp = Lx[i] + Ly[j] - g[i][j]; 34 if (!tmp) { 35 T[j] = true; 36 if (match[j] == -1 || dfs(match[j])) { 37 match[j] = i; 38 return true; 39 } 40 } 41 else slack[j] = min(slack[j], tmp); 42 } 43 return false; 44 } 45 46 void update() { 47 int a = INF; 48 for (int i = 0; i < n; i++) 49 if (!T[i]) a = min(a, slack[i]); 50 for (int i = 0; i < n; i++) { 51 if (S[i]) Lx[i] -= a; 52 if (T[i]) Ly[i] += a; 53 } 54 } 55 56 void km() { 57 for (int i = 0; i < n; i++) { 58 match[i] = -1; 59 Lx[i] = -INF; Ly[i] = 0; 60 for (int j = 0; j < n; j++) 61 Lx[i] = max(Lx[i], g[i][j]); 62 } 63 for (int i = 0; i < n; i++) { 64 for (int j = 0; j < n; j++) slack[j] = INF; 65 while (1) { 66 for (int j = 0; j < n; j++) S[j] = T[j] = false; 67 if (dfs(i)) break; 68 else update(); 69 } 70 } 71 } 72 }Men; 73 74 int main() { 75 int n; 76 while (scanf("%d", &n) == 1 && n) { 77 Men.init(n); 78 REP(u, 0, n) { 79 int v; 80 while (scanf("%d", &v) && v) { 81 int w; scanf("%d", &w); 82 v--; 83 Men.add_Edge(u, v, -w); 84 } 85 } 86 87 Men.km(); 88 int ans = 0, flag = 1; 89 REP(i, 0, n) { 90 if (Men.g[Men.match[i]][i] == -INF) { 91 //有未匹配到,就是不成功,因为题目要求的是完美匹配 92 flag = 0; 93 break; 94 } 95 ans += Men.g[Men.match[i]][i];//累加权值 96 } 97 if (!flag) printf("N "); 98 else printf("%d ", -ans);//最后是输出的是负数 99 } 100 return 0; 101 }
UVA12661
题意:
有一个赛车跑道,可以看做一个加权有向图。每个跑道(有向边)还有一个特点就是,会周期性地打开a秒,然后关闭b秒。只有在赛车进入一直到出来,该跑道一直处于打开状态,赛车才能通过。
开始时所有跑道处于刚打开的状态,求从起点到终点的最短时间。
解法:
因为每个点通过的时候需要等待一段时间,所以我们对于当前访问的每个点,计算得到它之前的所有时间, 之后%这个区间的总时间即是它目前的时间,判断是哪个区域并判断能否在关之前通过即可
向前星其实也不难撒hhh
1 #include<bits/stdc++.h> 2 #define REP(i, a, b) for(int i = (a); i < (b); i++) 3 #define MEM(a,x) memset(a,x,sizeof(a)) 4 #define INF 0x3f3f3f3f 5 #define MAXN 300+10 6 using namespace std; 7 8 struct Edge{ 9 int from, to, w, a, b; 10 int next; 11 }e[50000 + 5]; 12 int head[MAXN],vis[MAXN]; 13 int dis[MAXN]; 14 int n, m, tot; 15 16 void add_edge(int i, int j, int a,int b,int w) { 17 e[tot].from = i, e[tot].to = j, e[tot].w = w; 18 e[tot].a = a, e[tot].b = b; 19 e[tot].next = head[i]; head[i] = tot++; 20 } 21 22 void SPFA(int s){ 23 queue <int> q; 24 q.push(s); 25 dis[s] = 0; 26 while (!q.empty()){ 27 int u = q.front(); 28 q.pop(); 29 vis[u] = false; 30 for (int i = head[u]; i != -1; i = e[i].next) { 31 int v = e[i].to; 32 int plus = e[i].a + e[i].b; 33 int now = dis[u] % plus; 34 int wait; 35 if (now > (e[i].a - e[i].w)) wait = plus - now; 36 else wait = 0; 37 if (dis[v] > dis[u] + e[i].w + wait) { 38 dis[v] = dis[u] + e[i].w + wait; 39 if (!vis[v]) { 40 vis[v] = true; 41 q.push(v); 42 } 43 } 44 } 45 } 46 } 47 48 int main() { 49 int n, m, s, t, kase = 1; 50 while(scanf("%d%d%d%d", &n, &m, &s, &t)!=EOF) { 51 MEM(head, -1), MEM(dis, INF), MEM(vis, 0); 52 tot = 0; 53 REP(i, 0, m) { 54 int u, v, a, b, w; 55 scanf("%d%d%d%d%d", &u, &v, &a, &b, &w); 56 if (a >= w)add_edge(u, v, a, b, w); 57 } 58 SPFA(s); 59 printf("Case %d: %d ", kase++, dis[t]); 60 } 61 return 0; 62 }
UVA1515
题意:
给一个h*w的矩阵,每个格子中是‘#‘和‘.‘两个符号之一,分别代表草和洞。现在要将洞给围起来(将草和洞分离),每条边需花费b元(即将一个洞包起来需要4边,将2个连续的洞包起来需要6边,省了2条边)。有个特殊能力,能将洞变成草,花费f。当然也能将草变成洞,花费d。围起洞来需要多少花费。矩阵四周最边边的格子都必须是草,即出现洞就必须转草。
解法:
首先对所有边缘的点进行排查,把所有不是‘#’的都变成‘.’; 之后设定一个原点和汇点,把所有的草都与源点相连,容量为d,所有的洞都与汇点链接,容量为f, 边缘的草要进行特殊处理,容量为INF。
之后,对每个格子所有相邻的4个格子连一条容量为b的边,之后跑一边最大流即可
1 #include<bits/stdc++.h> 2 #define REP(i, a, b) for(int i = (a); i < (b); i++) 3 #define MEM(a,x) memset(a,x,sizeof(a)) 4 #define INF 0x3f3f3f3f 5 #define MAXN 3000 6 using namespace std; 7 8 struct Edge { 9 int from, to, cap, flow; 10 }; 11 struct Dinic { 12 int n, m, s, t; 13 vector<Edge>edges; 14 vector<int>G[MAXN]; 15 bool vis[MAXN]; 16 int d[MAXN]; 17 int cur[MAXN]; 18 void init(int n) { 19 for (int i = 0; i < n; i++) G[i].clear(); 20 edges.clear(); 21 } 22 void AddEdge(int from, int to, int cap) { 23 edges.push_back({ from, to, cap, 0 }); 24 edges.push_back({ to, from, 0, 0 }); 25 m = edges.size(); 26 G[from].push_back(m - 2); 27 G[to].push_back(m - 1); 28 } 29 bool BFS() { 30 int x, i; 31 memset(vis, 0, sizeof(vis)); 32 queue<int>Q; 33 Q.push(s); 34 d[s] = 0; 35 vis[s] = 1; 36 while (!Q.empty()) { 37 x = Q.front(), Q.pop(); 38 for (i = 0; i < G[x].size(); i++) { 39 Edge & e = edges[G[x][i]]; 40 if (!vis[e.to] && e.cap > e.flow) { 41 vis[e.to] = 1; 42 d[e.to] = d[x] + 1; 43 Q.push(e.to); 44 } 45 } 46 } 47 return vis[t]; 48 } 49 int DFS(int x, int a) { 50 if (x == t || a == 0) 51 return a; 52 int flow = 0, f; 53 for (int &i = cur[x]; i < G[x].size(); i++) { 54 Edge & e = edges[G[x][i]]; 55 if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) { 56 e.flow += f; 57 edges[G[x][i] ^ 1].flow -= f; 58 flow += f; 59 a -= f; 60 if (a == 0) 61 break; 62 } 63 } 64 return flow; 65 } 66 int Maxflow(int s, int t) { 67 this->s = s, this->t = t; 68 int flow = 0; 69 while (BFS()) { 70 memset(cur, 0, sizeof(cur)); 71 flow += DFS(s, INF); 72 } 73 return flow; 74 } 75 }; 76 77 int w, h, d, f, b; 78 char g[55][55]; 79 int ID(int i, int j) { return i*w + j; } 80 Dinic Men; 81 82 int main() { 83 int T; scanf("%d", &T); 84 while (T--) { 85 scanf("%d%d%d%d%d", &w, &h, &d, &f, &b); 86 REP(i, 0, h) scanf("%s", g[i]); 87 88 int cost = 0; 89 REP(i, 0, h) { 90 if (g[i][0] == ‘.‘) { g[i][0] = ‘#‘, cost += f; } 91 if (g[i][w - 1] == ‘.‘) { g[i][w - 1] = ‘#‘, cost += f; } 92 } 93 REP(j, 0, w) { 94 if (g[0][j] == ‘.‘) { g[0][j] = ‘#‘, cost += f; } 95 if (g[h - 1][j] == ‘.‘) { g[h - 1][j] = ‘#‘, cost += f; } 96 } 97 98 Men.init(w*h + 2); 99 int s = h*w, t = h*w + 1; 100 REP(i, 0, h)REP(j, 0, w) { 101 if (i == 0 || i == h - 1 || j == 0 || j == w - 1) 102 Men.AddEdge(s, ID(i, j), INF); 103 else if (g[i][j] == ‘#‘)Men.AddEdge(s, ID(i, j), d); 104 else Men.AddEdge(ID(i, j), t, f); 105 106 if (i > 0) Men.AddEdge(ID(i, j), ID(i - 1, j), b); 107 if (i < h - 1) Men.AddEdge(ID(i, j), ID(i + 1, j), b); 108 if (j > 0) Men.AddEdge(ID(i, j), ID(i, j - 1), b); 109 if (j < w - 1) Men.AddEdge(ID(i, j), ID(i, j + 1), b); 110 } 111 112 printf("%d ", cost + Men.Maxflow(s, t)); 113 114 } 115 return 0; 116 }
以上是关于9.1总结前日(数学+图论)的主要内容,如果未能解决你的问题,请参考以下文章